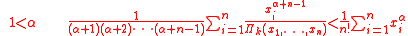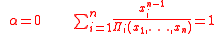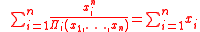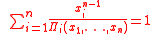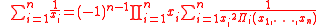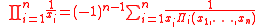Retkes identities
Encyclopedia
In mathematics, the Retkes identities, named after Zoltán Retkes, are one of the most efficient applications of the Retkes inequality
when
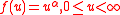 and
and  . In this special settings one can have for the iterated integrals
. In this special settings one can have for the iterated integrals
Since is strictly convex
is strictly convex
if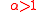 , strictly concave
, strictly concave
if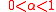 , linear
, linear
if hence the following inequalities and identities (mathematics) hold:
hence the following inequalities and identities (mathematics) hold:
One of the consequence of the case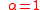 is the Retkes convergence criterion
is the Retkes convergence criterion
because of the right side of the equality is precisely the nth partial sum of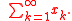
Assume henceforth that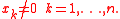 Under this condition substituting
Under this condition substituting 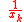 instead of
instead of 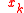 in the second and fourth identities one can have two universal algebraic identities. These four identities are the so called Retkes identities:
in the second and fourth identities one can have two universal algebraic identities. These four identities are the so called Retkes identities:
Hermite–Hadamard inequality
In mathematics, the Hermite–Hadamard inequality, named after Charles Hermite and Jacques Hadamard and sometimes also called Hadamard's inequality, states that if a function ƒ : [a, b] → R is convex, then...
when
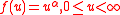 and
and  . In this special settings one can have for the iterated integrals
. In this special settings one can have for the iterated integralsHermite–Hadamard inequality
In mathematics, the Hermite–Hadamard inequality, named after Charles Hermite and Jacques Hadamard and sometimes also called Hadamard's inequality, states that if a function ƒ : [a, b] → R is convex, then...
Since
 is strictly convex
is strictly convexConvex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
if
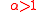 , strictly concave
, strictly concaveConcave function
In mathematics, a concave function is the negative of a convex function. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap or upper convex.-Definition:...
if
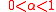 , linear
, linearLinear function
In mathematics, the term linear function can refer to either of two different but related concepts:* a first-degree polynomial function of one variable;* a map between two vector spaces that preserves vector addition and scalar multiplication....
if
 hence the following inequalities and identities (mathematics) hold:
hence the following inequalities and identities (mathematics) hold:One of the consequence of the case
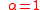 is the Retkes convergence criterion
is the Retkes convergence criterionRetkes convergence criterion
In mathematics, the Retkes convergence criterion, named after Zoltán Retkes, gives necessary and sufficient conditions for convergence of numerical series. Numerous criteria are known for testing convergence. The most famous of them is the so called Cauchy criterion, the only one that gives...
because of the right side of the equality is precisely the nth partial sum of
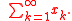
Assume henceforth that
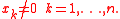 Under this condition substituting
Under this condition substituting 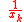 instead of
instead of 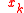 in the second and fourth identities one can have two universal algebraic identities. These four identities are the so called Retkes identities:
in the second and fourth identities one can have two universal algebraic identities. These four identities are the so called Retkes identities: