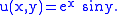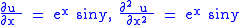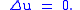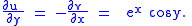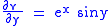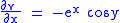Harmonic conjugate
Encyclopedia
In mathematics
, a function defined on some open domain
defined on some open domain  is said to have as a conjugate a function
is said to have as a conjugate a function 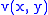 if and only if they are respectively real and imaginary part of a holomorphic function
if and only if they are respectively real and imaginary part of a holomorphic function 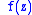 of the complex variable
of the complex variable 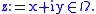 That is,
That is,  is conjugated to
is conjugated to  if
if 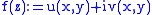 is holomorphic on
is holomorphic on  As a first consequence of the definition, they are both harmonic
As a first consequence of the definition, they are both harmonic
real-valued functions on . Moreover, the conjugate of
. Moreover, the conjugate of  if it exists, is unique up to an additive constant. Also,
if it exists, is unique up to an additive constant. Also,  is conjugate to
is conjugate to  if and only if
if and only if  is conjugate to
is conjugate to  .
.
Equivalently, is conjugate to
is conjugate to  in
in  if and only if
if and only if  and
and  satisfy the Cauchy–Riemann equations in
satisfy the Cauchy–Riemann equations in  As an immediate consequence of the latter equivalent definition, if
As an immediate consequence of the latter equivalent definition, if  is any harmonic function on
is any harmonic function on 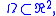 the function
the function 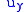 is conjugate to
is conjugate to 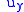 , for then the Cauchy–Riemann equations are just
, for then the Cauchy–Riemann equations are just 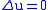 and the symmetry of the mixed second order derivatives,
and the symmetry of the mixed second order derivatives, 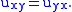 Therefore an harmonic function
Therefore an harmonic function  admits a conjugated harmonic function if and only if the holomorphic function
admits a conjugated harmonic function if and only if the holomorphic function 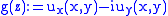 has a primitive
has a primitive 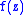 in
in  in which case a conjugate of
in which case a conjugate of  is, of course,
is, of course,  So any harmonic function always admits a conjugate function whenever its domain is simply connected, and in any case it admits a conjugate locally at any point of its domain.
So any harmonic function always admits a conjugate function whenever its domain is simply connected, and in any case it admits a conjugate locally at any point of its domain.
There is an operator taking a harmonic function u on a simply connected region in R2 to its harmonic conjugate v (putting e.g. v(x0)=0 on a given x0 in order to fix the indeterminacy of the conjugate up to constants). This is well known in applications as (essentially) the Hilbert transform
; it is also a basic example in mathematical analysis
, in connection with singular integral operators. Conjugate harmonic functions (and the transform between them) are also one of the simplest examples of a Bäcklund transform
(two PDEs and a transform relating their solutions), in this case linear; more complex transforms are of interest in soliton
s and integrable systems.
Geometrically u and v are related as having orthogonal trajectories, away from the zeroes of the underlying holomorphic function; the contours on which u and v are constant cross at right angle
s. In this regard, u+iv would be the complex potential, where u is the potential function
and v is the stream function
.
Since
and
it satisfies
and thus is harmonic. Now suppose we have a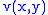 such that the Cauchy–Riemann equations are satisfied:
such that the Cauchy–Riemann equations are satisfied:
and
Simplifying,
and
which when solved gives
Observe that if the functions related to u and v were interchanged, the functions would not be harmonic conjugates, since the minus sign in the Cauchy–Riemann equations makes the relationship asymmetric.
The conformal mapping property of analytic function
s (at points where the derivative is not zero) gives rise to a geometric property of harmonic conjugates. Clearly the harmonic conjugate of x is y, and the lines of constant x and constant y are orthogonal. Conformality says that equally contour
s of constant u(x,y) and v(x,y) will also be orthogonal where they cross (away from the zeroes of f′(z)). That means that v is a specific solution of the orthogonal trajectory
problem for the family of contours given by u (not the only solution, naturally, since we can take also functions of v): the question, going back to the mathematics of the seventeenth century, of finding the curves that cross a given family of non-intersecting curves at right angle
s.
There is an additional occurrence of the term harmonic conjugate in mathematics
, and more specifically in geometry
. Two points A and B are said to be harmonic conjugates of each other with respect to another pair of points C, D if (ABCD) = −1, where (ABCD) is the cross-ratio
of points A, B, C, D (See Projective harmonic conjugates
.)
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a function
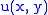 defined on some open domain
defined on some open domain 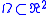 is said to have as a conjugate a function
is said to have as a conjugate a function 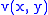 if and only if they are respectively real and imaginary part of a holomorphic function
if and only if they are respectively real and imaginary part of a holomorphic function 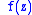 of the complex variable
of the complex variable 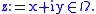 That is,
That is,  is conjugated to
is conjugated to  if
if 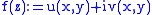 is holomorphic on
is holomorphic on  As a first consequence of the definition, they are both harmonic
As a first consequence of the definition, they are both harmonicHarmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
real-valued functions on
 . Moreover, the conjugate of
. Moreover, the conjugate of  if it exists, is unique up to an additive constant. Also,
if it exists, is unique up to an additive constant. Also,  is conjugate to
is conjugate to  if and only if
if and only if  is conjugate to
is conjugate to  .
.Equivalently,
 is conjugate to
is conjugate to  in
in  if and only if
if and only if  and
and  satisfy the Cauchy–Riemann equations in
satisfy the Cauchy–Riemann equations in  As an immediate consequence of the latter equivalent definition, if
As an immediate consequence of the latter equivalent definition, if  is any harmonic function on
is any harmonic function on 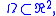 the function
the function 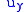 is conjugate to
is conjugate to 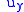 , for then the Cauchy–Riemann equations are just
, for then the Cauchy–Riemann equations are just 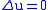 and the symmetry of the mixed second order derivatives,
and the symmetry of the mixed second order derivatives, 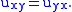 Therefore an harmonic function
Therefore an harmonic function  admits a conjugated harmonic function if and only if the holomorphic function
admits a conjugated harmonic function if and only if the holomorphic function 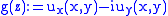 has a primitive
has a primitive 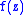 in
in 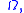 in which case a conjugate of
in which case a conjugate of  is, of course,
is, of course,  So any harmonic function always admits a conjugate function whenever its domain is simply connected, and in any case it admits a conjugate locally at any point of its domain.
So any harmonic function always admits a conjugate function whenever its domain is simply connected, and in any case it admits a conjugate locally at any point of its domain.There is an operator taking a harmonic function u on a simply connected region in R2 to its harmonic conjugate v (putting e.g. v(x0)=0 on a given x0 in order to fix the indeterminacy of the conjugate up to constants). This is well known in applications as (essentially) the Hilbert transform
Hilbert transform
In mathematics and in signal processing, the Hilbert transform is a linear operator which takes a function, u, and produces a function, H, with the same domain. The Hilbert transform is named after David Hilbert, who first introduced the operator in order to solve a special case of the...
; it is also a basic example in mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, in connection with singular integral operators. Conjugate harmonic functions (and the transform between them) are also one of the simplest examples of a Bäcklund transform
Bäcklund transform
In mathematics, Bäcklund transforms or Bäcklund transformations relate partial differential equations and their solutions. They are an important tool in soliton theory and integrable systems...
(two PDEs and a transform relating their solutions), in this case linear; more complex transforms are of interest in soliton
Soliton
In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
s and integrable systems.
Geometrically u and v are related as having orthogonal trajectories, away from the zeroes of the underlying holomorphic function; the contours on which u and v are constant cross at right angle
Right angle
In geometry and trigonometry, a right angle is an angle that bisects the angle formed by two halves of a straight line. More precisely, if a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles...
s. In this regard, u+iv would be the complex potential, where u is the potential function
Potential theory
In mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
and v is the stream function
Stream function
The stream function is defined for two-dimensional flows of various kinds. The stream function can be used to plot streamlines, which represent the trajectories of particles in a steady flow. Streamlines are perpendicular to equipotential lines...
.
Examples
For example, consider the functionSince
and
it satisfies
and thus is harmonic. Now suppose we have a
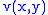 such that the Cauchy–Riemann equations are satisfied:
such that the Cauchy–Riemann equations are satisfied:
and
Simplifying,
and
which when solved gives
Observe that if the functions related to u and v were interchanged, the functions would not be harmonic conjugates, since the minus sign in the Cauchy–Riemann equations makes the relationship asymmetric.
The conformal mapping property of analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
s (at points where the derivative is not zero) gives rise to a geometric property of harmonic conjugates. Clearly the harmonic conjugate of x is y, and the lines of constant x and constant y are orthogonal. Conformality says that equally contour
Contour
Contour may refer to:* an outline or silhouette* a contour line on a contour map, or the corresponding line on the ground or sea bed* Contour , a phonetic sound* Pitch contour , a melody shape...
s of constant u(x,y) and v(x,y) will also be orthogonal where they cross (away from the zeroes of f′(z)). That means that v is a specific solution of the orthogonal trajectory
Orthogonal trajectory
In mathematics, orthogonal trajectories are a family of curves in the plane that intersect a given family of curves at right angles. The problem is classical, but is now understood by means of complex analysis; see for example harmonic conjugate....
problem for the family of contours given by u (not the only solution, naturally, since we can take also functions of v): the question, going back to the mathematics of the seventeenth century, of finding the curves that cross a given family of non-intersecting curves at right angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
s.
There is an additional occurrence of the term harmonic conjugate in mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and more specifically in geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
. Two points A and B are said to be harmonic conjugates of each other with respect to another pair of points C, D if (ABCD) = −1, where (ABCD) is the cross-ratio
Cross-ratio
In geometry, the cross-ratio, also called double ratio and anharmonic ratio, is a special number associated with an ordered quadruple of collinear points, particularly points on a projective line...
of points A, B, C, D (See Projective harmonic conjugates
Projective harmonic conjugates
In projective geometry, the harmonic conjugate point of a triple of points on the real projective line is defined by the following construction due to Karl von Staudt:...
.)