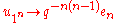Hall polynomial
Encyclopedia
In mathematics
the Hall algebra is an associative algebra
with a basis corresponding to isomorphism classes of finite abelian p-groups. It was first discussed by E. but forgotten until it was rediscovered by , both of whom published no more than brief summaries of their work. The Hall polynomials are the structure constants of the Hall algebra. The Hall algebra plays an important role in the theory of Kashiwara
–Lusztig's canonical bases in quantum group
s. generalized Hall algebras to more general categories, such as the category of representations of a quiver.
p-group
M is a direct sum of cyclic
p-power components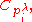 where
where
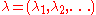 is a partition
is a partition
of called the type of M. Let
called the type of M. Let  be the number of subgroups N of M such that N has type
be the number of subgroups N of M such that N has type  and the quotient M/N has type
and the quotient M/N has type  . Hall proved that the functions g are polynomial
. Hall proved that the functions g are polynomial
functions of p with integer coefficients. Thus we may replace p with an indeterminate q, which results in the Hall polynomials
Hall next constructs an associative ring over
over 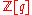 , now called the Hall algebra. This ring has a basis consisting of the symbols
, now called the Hall algebra. This ring has a basis consisting of the symbols  and the structure constants of the multiplication in this basis are given by the Hall polynomials:
and the structure constants of the multiplication in this basis are given by the Hall polynomials:

It turns out that H is a commutative ring, freely generated by the elements corresponding to the elementary p-groups
corresponding to the elementary p-groups
. The linear map from H to the algebra of symmetric function
s defined on the generators by the formula
(where en is the nth elementary symmetric function) uniquely extends to a ring homomorphism
and the images of the basis elements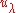 may be interpreted via the Hall–Littlewood symmetric functions
may be interpreted via the Hall–Littlewood symmetric functions
. Specializing q to 1, these symmetric functions become Schur functions, which are thus closely connected with the theory of Hall polynomials.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
the Hall algebra is an associative algebra
Associative algebra
In mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
with a basis corresponding to isomorphism classes of finite abelian p-groups. It was first discussed by E. but forgotten until it was rediscovered by , both of whom published no more than brief summaries of their work. The Hall polynomials are the structure constants of the Hall algebra. The Hall algebra plays an important role in the theory of Kashiwara
Masaki Kashiwara
is a Japanese mathematician. He was a student of Mikio Sato at the University of Tokyo. Sato and Kashiwara have collaborated on algebraic analysis and D-module theory.He is a member of the French Academy of Sciences.- Concepts named after Kashiwara :...
–Lusztig's canonical bases in quantum group
Quantum group
In mathematics and theoretical physics, the term quantum group denotes various kinds of noncommutative algebra with additional structure. In general, a quantum group is some kind of Hopf algebra...
s. generalized Hall algebras to more general categories, such as the category of representations of a quiver.
Construction
A finite abelianAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
p-group
P-group
In mathematics, given a prime number p, a p-group is a periodic group in which each element has a power of p as its order: each element is of prime power order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power pn is equal to the identity element...
M is a direct sum of cyclic
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
p-power components
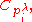 where
where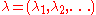 is a partition
is a partitionPartition (number theory)
In number theory and combinatorics, a partition of a positive integer n, also called an integer partition, is a way of writing n as a sum of positive integers. Two sums that differ only in the order of their summands are considered to be the same partition; if order matters then the sum becomes a...
of
 called the type of M. Let
called the type of M. Let  be the number of subgroups N of M such that N has type
be the number of subgroups N of M such that N has type  and the quotient M/N has type
and the quotient M/N has type  . Hall proved that the functions g are polynomial
. Hall proved that the functions g are polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
functions of p with integer coefficients. Thus we may replace p with an indeterminate q, which results in the Hall polynomials
Hall next constructs an associative ring
 over
over 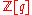 , now called the Hall algebra. This ring has a basis consisting of the symbols
, now called the Hall algebra. This ring has a basis consisting of the symbols  and the structure constants of the multiplication in this basis are given by the Hall polynomials:
and the structure constants of the multiplication in this basis are given by the Hall polynomials:
It turns out that H is a commutative ring, freely generated by the elements
 corresponding to the elementary p-groups
corresponding to the elementary p-groupsElementary Abelian group
In group theory, an elementary abelian group is a finite abelian group, where every nontrivial element has order p, where p is a prime; in particular it is a p-group....
. The linear map from H to the algebra of symmetric function
Symmetric function
In algebra and in particular in algebraic combinatorics, the ring of symmetric functions, is a specific limit of the rings of symmetric polynomials in n indeterminates, as n goes to infinity...
s defined on the generators by the formula
(where en is the nth elementary symmetric function) uniquely extends to a ring homomorphism
Ring homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
and the images of the basis elements
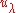 may be interpreted via the Hall–Littlewood symmetric functions
may be interpreted via the Hall–Littlewood symmetric functionsHall–Littlewood polynomial
In mathematics, the Hall–Littlewood polynomials are symmetric functions depending on a parameter t and a partition λ. They are Schur functions when t is 0 and monomial symmetric functions when t is 1 and are special cases of Macdonald polynomials.They were first defined indirectly by ...
. Specializing q to 1, these symmetric functions become Schur functions, which are thus closely connected with the theory of Hall polynomials.