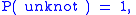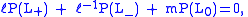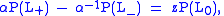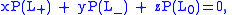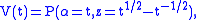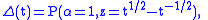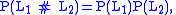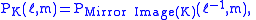HOMFLY polynomial
Encyclopedia
In the mathematical
field of knot theory
, the HOMFLY polynomial, sometimes called the HOMFLY-PT polynomial or the generalized Jones polynomial, is a 2-variable knot polynomial
, i.e. a knot invariant
in the form of a polynomial
of variables m and l.
A central question in the mathematical theory of knots
is whether two knot diagrams represent the same knot. One tool used to answer such questions is a knot polynomial, which is computed from a diagram of the knot and can be shown to be an invariant of the knot
, i.e. if two diagrams have different polynomial
s, they represent different knots. The converse may not be true. The HOMFLY polynomial is one such invariant and it generalizes two polynomials previously discovered, the Alexander polynomial
and the Jones polynomial both of which can be obtained by appropriate substitutions from HOMFLY. The HOMFLY polynomial is also a quantum invariant
.
The name HOMFLY combines the initials of its co-discoverers: Jim Hoste, Adrian Ocneanu, Kenneth Millett, Peter J. Freyd
, W. B. R. Lickorish, and David Nelson Yetter. The addition of PT recognizes independent work carried out by Józef H. Przytycki
and Paweł Traczyk.
s:
where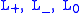 are crossing and smoothing changes on a local region of a link diagram, as indicated in the figure.
are crossing and smoothing changes on a local region of a link diagram, as indicated in the figure. .svg.png) The HOMFLY polynomial of a link L that is a split union of two links
The HOMFLY polynomial of a link L that is a split union of two links 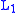 and
and  is given by
is given by 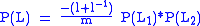 .
.
See the page on skein relation
for an example of a computation using these relations.
where V(t) is the Jones polynomial.
where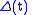 is the Alexander polynomial.
is the Alexander polynomial.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of knot theory
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
, the HOMFLY polynomial, sometimes called the HOMFLY-PT polynomial or the generalized Jones polynomial, is a 2-variable knot polynomial
Knot polynomial
In the mathematical field of knot theory, a knot polynomial is a knot invariant in the form of a polynomial whose coefficients encode some of the properties of a given knot.-History:The first knot polynomial, the Alexander polynomial, was introduced by J. W...
, i.e. a knot invariant
Knot invariant
In the mathematical field of knot theory, a knot invariant is a quantity defined for each knot which is the same for equivalent knots. The equivalence is often given by ambient isotopy but can be given by homeomorphism. Some invariants are indeed numbers, but invariants can range from the...
in the form of a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
of variables m and l.
A central question in the mathematical theory of knots
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
is whether two knot diagrams represent the same knot. One tool used to answer such questions is a knot polynomial, which is computed from a diagram of the knot and can be shown to be an invariant of the knot
Knot invariant
In the mathematical field of knot theory, a knot invariant is a quantity defined for each knot which is the same for equivalent knots. The equivalence is often given by ambient isotopy but can be given by homeomorphism. Some invariants are indeed numbers, but invariants can range from the...
, i.e. if two diagrams have different polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s, they represent different knots. The converse may not be true. The HOMFLY polynomial is one such invariant and it generalizes two polynomials previously discovered, the Alexander polynomial
Alexander polynomial
In mathematics, the Alexander polynomial is a knot invariant which assigns a polynomial with integer coefficients to each knot type. James Waddell Alexander II discovered this, the first knot polynomial, in 1923...
and the Jones polynomial both of which can be obtained by appropriate substitutions from HOMFLY. The HOMFLY polynomial is also a quantum invariant
Quantum invariant
In the mathematical field of knot theory, a quantum invariant of a knot or link is a linear sum of colored Jones polynomial of surgery presentations of the knot complement.-List of invariants:*Finite type invariant*Kontsevich invariant*Kashaev's invariant...
.
The name HOMFLY combines the initials of its co-discoverers: Jim Hoste, Adrian Ocneanu, Kenneth Millett, Peter J. Freyd
Peter J. Freyd
Peter J. Freyd is an American mathematician, a professor at the University of Pennsylvania, known for work in category theory and for founding the False Memory Syndrome Foundation.- Mathematical work :...
, W. B. R. Lickorish, and David Nelson Yetter. The addition of PT recognizes independent work carried out by Józef H. Przytycki
Józef H. Przytycki
Józef Henryk Przytycki , is a mathematician specializing in the fields of knot theory and topology.In 1987, he and Pawel Traczyk published "Invariants of links of Conway type" , which included a description of what is now called the HOMFLY polynomial...
and Paweł Traczyk.
Definition
The polynomial is defined using skein relationSkein relation
A central question in the mathematical theory of knots is whether two knot diagrams represent the same knot. One tool used to answer such questions is a knot polynomial which is an invariant of the knot. If two diagrams have different polynomials, they represent different knots. The reverse may not...
s:
where
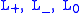 are crossing and smoothing changes on a local region of a link diagram, as indicated in the figure.
are crossing and smoothing changes on a local region of a link diagram, as indicated in the figure. .svg.png)
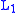 and
and  is given by
is given by 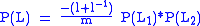 .
.See the page on skein relation
Skein relation
A central question in the mathematical theory of knots is whether two knot diagrams represent the same knot. One tool used to answer such questions is a knot polynomial which is an invariant of the knot. If two diagrams have different polynomials, they represent different knots. The reverse may not...
for an example of a computation using these relations.
Other HOMFLY skein relations
This polynomial can be obtained also using other skein relations:Main properties
where V(t) is the Jones polynomial.
where
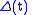 is the Alexander polynomial.
is the Alexander polynomial.