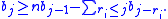In mathematics, the Golod–Shafarevich theorem was proved in 1964 by two Russia

Russia

Russia or , officially known as both Russia and the Russian Federation , is a country in northern Eurasia. It is a federal semi-presidential republic, comprising 83 federal subjects...

n mathematicians, Evgeny Golod

Evgeny Golod

Evgenii Solomonovich Golod is a Russian mathematician who proved the Golod–Shafarevich theorem on class field towers. As an application, he gave a negative solution to the Kurosh–Levitzky problem on the nilpotency of finitely generated nil algebras, and so to a weak form of Burnside's problem....

 and Igor Shafarevich

Igor Shafarevich

Igor Rostislavovich Shafarevich is a Soviet and Russian mathematician, founder of a school of algebraic number theory and algebraic geometry in the USSR, and a political writer. He was also an important dissident figure under the Soviet regime, a public supporter of Andrei Sakharov's Human Rights...

. It is a result in non-commutative homological algebra

Homological algebra

Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...

 which has consequences in various branches of algebra

Algebra

Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...

.

The inequality

Let A = K<x₁, ..., x_n> be the free algebra

Free algebra

In mathematics, especially in the area of abstract algebra known as ring theory, a free algebra is the noncommutative analogue of a polynomial ring .-Definition:...

 over a field

Field (mathematics)

In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...

 K in n = d + 1 non-commuting variables x_i.

Let J be the 2-sided ideal of A generated by homogeneous elements f_j of A of degree d_j with

2 ≤ d₁ ≤ d₂ ≤ ...

where d_j tends to infinity. Let r_i be the number of d_j equal to i.

Let B=A/J, a graded algebra

Graded algebra

In mathematics, in particular abstract algebra, a graded algebra is an algebra over a field with an extra piece of structure, known as a gradation ....

. Let b_j = dim B_j.

The fundamental inequality of Golod and Shafarevich states that

As a consequence:

• B is infinite-dimensional if r_i ≤ d²/4 for all i

• if B is finite-dimensional, then r_i > d²/4 for some i.

Applications

This result has important applications in combinatorial group theory

Combinatorial group theory

In mathematics, combinatorial group theory is the theory of free groups, and the concept of a presentation of a group by generators and relations...

:

• If G is a nontrivial finite p-group
  P-group
  In mathematics, given a prime number p, a p-group is a periodic group in which each element has a power of p as its order: each element is of prime power order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power pn is equal to the identity element...
  
  , then r > d²/4 where d = dim H¹(G,Z/pZ) and r = dim H²(G,Z/pZ) (the mod p cohomology groups
  Group cohomology
  In abstract algebra, homological algebra, algebraic topology and algebraic number theory, as well as in applications to group theory proper, group cohomology is a way to study groups using a sequence of functors H n. The study of fixed points of groups acting on modules and quotient modules...
  
   of G). In particular if G is a finite p-group
  P-group
  In mathematics, given a prime number p, a p-group is a periodic group in which each element has a power of p as its order: each element is of prime power order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power pn is equal to the identity element...
  
   with minimal number of generators d and has r relators in a given presentation, then r > d²/4.

• For each prime p, there is an infinite group G generated by three elements in which each element has order a power of p. The group G provides a counterexample to the generalised Burnside conjecture
  Burnside's problem
  The Burnside problem, posed by William Burnside in 1902 and one of the oldest and most influential questions in group theory, asks whether a finitely generated group in which every element has finite order must necessarily be a finite group...
  
  : it is a finitely generated
  Finitely generated
  In mathematics, finitely generated may refer to:* Finitely generated group* Finitely generated monoid* Finitely generated abelian group* Finitely generated module* Finitely generated ideal* Finitely generated algebra* Finitely generated space...
  
   infinite torsion group, although there is no uniform bound on the order of its elements.

In class field theory

Class field theory

In mathematics, class field theory is a major branch of algebraic number theory that studies abelian extensions of number fields.Most of the central results in this area were proved in the period between 1900 and 1950...

, the class field tower of a number field K is created by iterating the Hilbert class field

Hilbert class field

In algebraic number theory, the Hilbert class field E of a number field K is the maximal abelian unramified extension of K. Its degree over K equals the class number of K and the Galois group of E over K is canonically isomorphic to the ideal class group of K using Frobenius elements for prime...

 construction. Another consequence of the construction is that such towers may be infinite (in other words, do not always terminate in a field equal to its Hilbert

David Hilbert

David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...

class field).