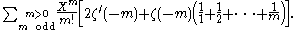Arakelov theory
Encyclopedia
Arakelov theory is an approach to Diophantine geometry
, named for Suren Arakelov
. It is used to study Diophantine equations in higher dimensions.
X over the ring of integers Z, by putting Hermitian metrics on holomorphic vector bundle
s over X(C), the complex points of X. This extra Hermitian structure is applied as a substitute, for the failure of the scheme Spec(Z) to be a complete variety.
in the case of number fields. In , Faltings extended Arakelov's work by establishing results such as a Riemann-Roch theorem, a Noether formula, a Hodge index theorem and the nonnegativity of the self-intersection of the dualizing sheaf in this context.
Arakelov theory was used by Paul Vojta
(1991) to give a new proof of the Mordell conjecture, and by in his proof of Lang's generalization of the Mordell conjecture.
In , Deligne developed a more general framework to define the intersection pairing defined on an arithmetic surface over the spectrum of a ring of integers by Arakelov.
Arakelov's theory was generalized by Gillet and Soulé to higher dimensions. That is, Gillet and Soulé defined an intersection pairing on an arithmetic variety. One of the main results of Gillet and Soulé is the arithmetic Riemann–Roch theorem of , an extension of the Grothendieck–Riemann–Roch theorem to arithmetic varieties.
For this one defines arithmetic Chow group
s CHp(X) of an arithmetic variety X, and defines Chern class
es for Hermitian vector bundles over X taking values in the arithmetic Chow groups.
The arithmetic Riemann–Roch theorem then describes how the Chern class behaves under pushforward of vector bundles under a proper map of arithmetic varieties. A complete proof of this theorem was only published recently by Gillet, Rössler and Soulé.
Arakelov's intersection theory for arithmetic surfaces was developed further by Bost . The theory of Bost is based on the use of Green functions which, up to logarithmic singularities, belong to the Sobolev space L21. In this context Bost obtains an arithmetic Hodge index theorem and uses this to obtain Lefschetz theorems for arithmetic surfaces.
. The arithmetic Chow group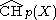 of codimension p is the quotient of this group by the subgroup generated by certain "trivial" cycles.
of codimension p is the quotient of this group by the subgroup generated by certain "trivial" cycles.
The arithmetic Riemann–Roch theorem states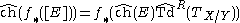
where
Diophantine geometry
In mathematics, diophantine geometry is one approach to the theory of Diophantine equations, formulating questions about such equations in terms of algebraic geometry over a ground field K that is not algebraically closed, such as the field of rational numbers or a finite field, or more general...
, named for Suren Arakelov
Suren Arakelov
Suren Yurievich Arakelov is a mathematician, best known for the influential theory that bears his name. Arakelov theory was exploited by Paul Vojta to give a new proof of the Mordell conjecture and by Gerd Faltings in his proof of Lang's generalization of the Mordell conjecture.From 1965...
. It is used to study Diophantine equations in higher dimensions.
Background
Arakelov geometry studies a schemeScheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
X over the ring of integers Z, by putting Hermitian metrics on holomorphic vector bundle
Holomorphic vector bundle
In mathematics, a holomorphic vector bundle is a complex vector bundle over a complex manifold X such that the total space E is a complex manifold and the projection map \pi:E\to X is holomorphic. Fundamental examples are the holomorphic tangent bundle of a complex manifold, and its dual, the...
s over X(C), the complex points of X. This extra Hermitian structure is applied as a substitute, for the failure of the scheme Spec(Z) to be a complete variety.
Results
In Arakelov defined an intersection theory on the arithmetic surfaces attached to smooth projective curves over number fields, with the aim of proving certain results, known in the case of functions fields,in the case of number fields. In , Faltings extended Arakelov's work by establishing results such as a Riemann-Roch theorem, a Noether formula, a Hodge index theorem and the nonnegativity of the self-intersection of the dualizing sheaf in this context.
Arakelov theory was used by Paul Vojta
Paul Vojta
Paul Alan Vojta is an American mathematician, known for his work in number theory on diophantine geometry and diophantine approximation....
(1991) to give a new proof of the Mordell conjecture, and by in his proof of Lang's generalization of the Mordell conjecture.
In , Deligne developed a more general framework to define the intersection pairing defined on an arithmetic surface over the spectrum of a ring of integers by Arakelov.
Arakelov's theory was generalized by Gillet and Soulé to higher dimensions. That is, Gillet and Soulé defined an intersection pairing on an arithmetic variety. One of the main results of Gillet and Soulé is the arithmetic Riemann–Roch theorem of , an extension of the Grothendieck–Riemann–Roch theorem to arithmetic varieties.
For this one defines arithmetic Chow group
Chow ring
In algebraic geometry, the Chow ring of an algebraic variety is an algebraic-geometric analogue of the cohomology ring of the variety considered as a topological space: its elements are formed out of actual subvarieties and its multiplicative structure is derived from the intersection of...
s CHp(X) of an arithmetic variety X, and defines Chern class
Chern class
In mathematics, in particular in algebraic topology and differential geometry, the Chern classes are characteristic classes associated to complex vector bundles.Chern classes were introduced by .-Basic idea and motivation:...
es for Hermitian vector bundles over X taking values in the arithmetic Chow groups.
The arithmetic Riemann–Roch theorem then describes how the Chern class behaves under pushforward of vector bundles under a proper map of arithmetic varieties. A complete proof of this theorem was only published recently by Gillet, Rössler and Soulé.
Arakelov's intersection theory for arithmetic surfaces was developed further by Bost . The theory of Bost is based on the use of Green functions which, up to logarithmic singularities, belong to the Sobolev space L21. In this context Bost obtains an arithmetic Hodge index theorem and uses this to obtain Lefschetz theorems for arithmetic surfaces.
Arithmetic Chow groups
An arithmetic cycle of codimension p is a pair (Z, g) where Z ∈ Zp(X) is a p-cycle on X and g is a Green current for Z, a higher dimensional generalization of a Green functionGreen function
Green function might refer to:*Green's function of a differential operator.*Deligne–Lusztig theory in the representation theory of finite groups of Lie type.*Green's function in many-body theory....
. The arithmetic Chow group
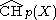 of codimension p is the quotient of this group by the subgroup generated by certain "trivial" cycles.
of codimension p is the quotient of this group by the subgroup generated by certain "trivial" cycles.The arithmetic Riemann–Roch theorem
The usual Grothendieck–Riemann–Roch theorem describes how the Chern character ch behaves under pushforward of sheaves, and states that ch(f*(E))= f*(ch(E)TdX/Y), where f is a proper morphism from X to Y and E is a vector bundle over f. The arithmetic Riemann–Roch theorem is similar except that the Todd class gets multiplied by a certain power series.The arithmetic Riemann–Roch theorem states
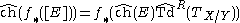
where
- X and Y are regular projective arithmetic schemes.
- f is a smooth proper map from X to Y
- E is an arithmetic vector bundle over X.
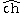 is the arithmetic Chern character.
is the arithmetic Chern character.- TX/Y is the relative tangent bundle
 is the arithmetic Todd classTodd classIn mathematics, the Todd class is a certain construction now considered a part of the theory in algebraic topology of characteristic classes. The Todd class of a vector bundle can be defined by means of the theory of Chern classes, and is encountered where Chern classes exist — most notably...
is the arithmetic Todd classTodd classIn mathematics, the Todd class is a certain construction now considered a part of the theory in algebraic topology of characteristic classes. The Todd class of a vector bundle can be defined by means of the theory of Chern classes, and is encountered where Chern classes exist — most notably...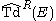 is
is 
- R(X) is the additive characteristic class associated to the formal power series