Generalized minimal residual method
Encyclopedia
In mathematics, the generalized minimal residual method (usually abbreviated GMRES) is an iterative method
for the numerical
solution of a system of linear equations. The method approximates the solution by the vector in a Krylov subspace
with minimal residual. The Arnoldi iteration
is used to find this vector.
The GMRES method was developed by Yousef Saad
and Martin H. Schultz in 1986.
GMRES is a special case of the DIIS
method developed by Peter Pulay in 1980. The latter method is also applicable to non-linear systems.
The matrix A is assumed to be invertible of size m-by-m. Furthermore, it is assumed that b is normalized, i.e., that ||b|| = 1.
The nth Krylov subspace for this problem is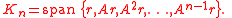
GMRES approximates the exact solution of Ax = b by the vector xn ∈ Kn that minimizes the Euclidean norm of the residual Axn − b.
The vectors r, Ar, …, An−1r might be almost linearly dependent
, so instead of this basis, the Arnoldi iteration
is used to find orthonormal vectors
which form a basis for Kn. Hence, the vector xn ∈ Kn can be written as xn = Qnyn with yn ∈ Rn, where Qn is the m-by-n matrix formed by q1, …, qn.
The Arnoldi process also produces an (n+1)-by-n upper Hessenberg matrix
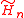with
Because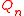
is orthogonal, we have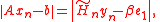
where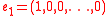
is the first vector in the standard basis
of Rn+1, and
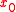being the first trial vector (usually zero). Hence, 
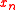can be found by minimizing the Euclidean norm of the residual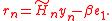
This is a linear least squares
problem of size n.
This yields the GMRES method. At every step of the iteration:
At every iteration, a matrix-vector product Aqn must be computed. This costs about 2m2 floating-point operations
for general dense matrices of size m, but the cost can decrease to O(m) for sparse matrices
. In addition to the matrix-vector product, O(n m) floating-point operations must be computed at the nth iteration.
exact solution.
This does not happen in general. Indeed, a theorem of Greenbaum, Pták and Strakoš states that for every monotonically decreasing sequence a1, …, am−1, am = 0, one can find a matrix A such that the ||rn|| = an for all n, where rn is the residual defined above. In particular, it is possible to find a matrix for which the residual stays constant for m − 1 iterations, and only drops to zero at the last iteration.
In practice, though, GMRES often performs well. This can be proven in specific situations. If A is positive definite
, then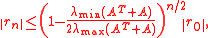
where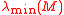
and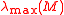 
denote the smallest and largest eigenvalue of the matrix 
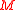, respectively.
If A is symmetric and positive definite, then we even have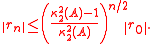
where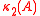
denotes the condition number
of A in the Euclidean norm.
In the general case, where A is not positive definite, we have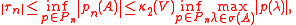
where Pn denotes the set of polynomials of degree at most n with p(0) = 1, V is the matrix appearing in the spectral decomposition of A, and σ(A) is the spectrum
of A. Roughly speaking, this says that fast convergence occurs when the eigenvalues of A are clustered away from the origin and A is not too far from normality
.
All these inequalities bound only the residuals instead of the actual error, that is, the distance between the current iterate xn and the exact solution.
The cost of the iterations grow like O(n2), where n is the iteration number. Therefore, the method is sometimes restarted after a number, say k, of iterations, with xk as initial guess. The resulting method is called GMRES(k).
Another class of methods builds on the unsymmetric Lanczos iteration, in particular the BiCG method
. These use a three-term recurrence relation, but they do not attain the minimum residual, and hence the residual does not decrease monotonically for these methods. Convergence is not even guaranteed.
The third class is formed by methods like CGS and BiCGSTAB
. These also work with a three-term recurrence relation (hence, without optimality) and they can even terminate prematurely without achieving convergence. The idea behind these methods is to choose the generating polynomials of the iteration sequence suitably.
None of these three classes is the best for all matrices; there are always examples in which one class outperforms the other. Therefore, multiple solvers are tried in practice to see which one is the best for a given problem.
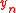which minimizes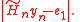
Note that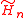
is an (n+1)-by-n matrix, hence it gives an over-constrained linear system of n+1 equations for n unknowns.
The minimum can be computed using a QR decomposition
: find an (n+1)-by-(n+1) orthogonal matrix
Ωn and an (n+1)-by-n upper triangular matrix
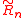such that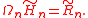
The triangular matrix has one more row than it has columns, so its bottom row consists of zero. Hence, it can be decomposed as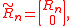
where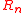
is an n-by-n (thus square) triangular matrix.
The QR decomposition can be updated cheaply from one iteration to the next, because the Hessenberg matrices differ only by a row of zeros and a column: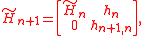
where hn = (h1n, … hnn)T. This implies that premultiplying the Hessenberg matrix with Ωn, augmented with zeroes and a row with multiplicative identity, yields almost a triangular matrix: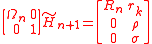
This would be triangular if σ is zero. To remedy this, one needs the Givens rotation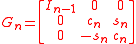
where
With this Givens rotation, we form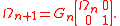
Indeed,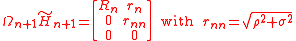
is a triangular matrix.
Given the QR decomposition, the minimization problem is easily solved by noting that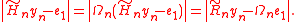
Denoting the vector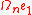
by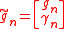
with gn ∈ Rn and γn ∈ R, this is
The vector y that minimizes this expression is given by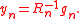
Again, the vectors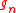
are easy to update.
Iterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
for the numerical
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
solution of a system of linear equations. The method approximates the solution by the vector in a Krylov subspace
Krylov subspace
In linear algebra, the order-r Krylov subspace generated by an n-by-n matrix A and a vector b of dimension n is the linear subspace spanned by the images of b under the first r powers of A , that is,...
with minimal residual. The Arnoldi iteration
Arnoldi iteration
In numerical linear algebra, the Arnoldi iteration is an eigenvalue algorithm and an important example of iterative methods. Arnoldi finds the eigenvalues of general matrices; an analogous method for Hermitian matrices is the Lanczos iteration. The Arnoldi iteration was invented by W. E...
is used to find this vector.
The GMRES method was developed by Yousef Saad
Yousef Saad
Yousef Saad is an I.T. Distinguished Professor of Computer Science in the Department of Computer Science and Engineering at the University of Minnesota. He holds the William Norris Chair for Large-Scale Computing since January 2006...
and Martin H. Schultz in 1986.
GMRES is a special case of the DIIS
DIIS
DIIS , also known as Pulay mixing, is an extrapolation technique...
method developed by Peter Pulay in 1980. The latter method is also applicable to non-linear systems.
The method
Denote the Euclidean norm of any vector v by ||v||. Denote the system of linear equations to be solved byThe matrix A is assumed to be invertible of size m-by-m. Furthermore, it is assumed that b is normalized, i.e., that ||b|| = 1.
The nth Krylov subspace for this problem is
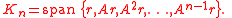
GMRES approximates the exact solution of Ax = b by the vector xn ∈ Kn that minimizes the Euclidean norm of the residual Axn − b.
The vectors r, Ar, …, An−1r might be almost linearly dependent
Linear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
, so instead of this basis, the Arnoldi iteration
Arnoldi iteration
In numerical linear algebra, the Arnoldi iteration is an eigenvalue algorithm and an important example of iterative methods. Arnoldi finds the eigenvalues of general matrices; an analogous method for Hermitian matrices is the Lanczos iteration. The Arnoldi iteration was invented by W. E...
is used to find orthonormal vectors
which form a basis for Kn. Hence, the vector xn ∈ Kn can be written as xn = Qnyn with yn ∈ Rn, where Qn is the m-by-n matrix formed by q1, …, qn.
The Arnoldi process also produces an (n+1)-by-n upper Hessenberg matrix
Hessenberg matrix
In linear algebra, a Hessenberg matrix is a special kind of square matrix, one that is "almost" triangular. To be exact, an upper Hessenberg matrix has zero entries below the first subdiagonal, and a lower Hessenberg matrix has zero entries above the first superdiagonal...
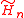withBecause
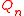is orthogonal, we have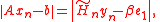where
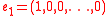
is the first vector in the standard basis
Standard basis
In mathematics, the standard basis for a Euclidean space consists of one unit vector pointing in the direction of each axis of the Cartesian coordinate system...
of Rn+1, and
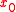being the first trial vector (usually zero). Hence, 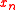can be found by minimizing the Euclidean norm of the residual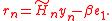This is a linear least squares
Linear least squares
In statistics and mathematics, linear least squares is an approach to fitting a mathematical or statistical model to data in cases where the idealized value provided by the model for any data point is expressed linearly in terms of the unknown parameters of the model...
problem of size n.
This yields the GMRES method. At every step of the iteration:
- do one step of the Arnoldi method;
- find the
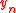which minimizes ||rn||; - compute
; - repeat if the residual is not yet small enough.
At every iteration, a matrix-vector product Aqn must be computed. This costs about 2m2 floating-point operations
Floating point
In computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...
for general dense matrices of size m, but the cost can decrease to O(m) for sparse matrices
Sparse matrix
In the subfield of numerical analysis, a sparse matrix is a matrix populated primarily with zeros . The term itself was coined by Harry M. Markowitz....
. In addition to the matrix-vector product, O(n m) floating-point operations must be computed at the nth iteration.
Convergence
The nth iterate minimizes the residual in the Krylov subspace Kn. Since every subspace is contained in the next subspace, the residual decreases monotonically. After m iterations, where m is the size of the matrix A, the Krylov space Km is the whole of Rm and hence the GMRES method arrives at the exact solution. However, the idea is that after a small number of iterations (relative to m), the vector xn is already a good approximation to theexact solution.
This does not happen in general. Indeed, a theorem of Greenbaum, Pták and Strakoš states that for every monotonically decreasing sequence a1, …, am−1, am = 0, one can find a matrix A such that the ||rn|| = an for all n, where rn is the residual defined above. In particular, it is possible to find a matrix for which the residual stays constant for m − 1 iterations, and only drops to zero at the last iteration.
In practice, though, GMRES often performs well. This can be proven in specific situations. If A is positive definite
Positive-definite matrix
In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
, then
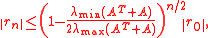
where
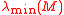and 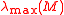denote the smallest and largest eigenvalue of the matrix 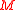, respectively.If A is symmetric and positive definite, then we even have
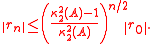
where
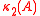denotes the condition numberCondition number
In the field of numerical analysis, the condition number of a function with respect to an argument measures the asymptotically worst case of how much the function can change in proportion to small changes in the argument...
of A in the Euclidean norm.
In the general case, where A is not positive definite, we have
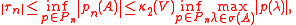
where Pn denotes the set of polynomials of degree at most n with p(0) = 1, V is the matrix appearing in the spectral decomposition of A, and σ(A) is the spectrum
Spectrum of a matrix
In mathematics, the spectrum of a matrix is the set of its eigenvalues. This notion can be extended to the spectrum of an operator in the infinite-dimensional case.The determinant equals the product of the eigenvalues...
of A. Roughly speaking, this says that fast convergence occurs when the eigenvalues of A are clustered away from the origin and A is not too far from normality
Normal matrix
A complex square matrix A is a normal matrix ifA^*A=AA^* \ where A* is the conjugate transpose of A. That is, a matrix is normal if it commutes with its conjugate transpose.If A is a real matrix, then A*=AT...
.
All these inequalities bound only the residuals instead of the actual error, that is, the distance between the current iterate xn and the exact solution.
Extensions of the method
Like other iterative methods, GMRES is usually combined with a preconditioning method in order to speed up convergence.The cost of the iterations grow like O(n2), where n is the iteration number. Therefore, the method is sometimes restarted after a number, say k, of iterations, with xk as initial guess. The resulting method is called GMRES(k).
Comparison with other solvers
The Arnoldi iteration reduces to the Lanczos iteration for symmetric matrices. The corresponding Krylov subspace method is the minimal residual method (MinRes) of Paige and Saunders. Unlike the unsymmetric case, the MinRes method is given by a three-term recurrence relation. It can be shown that there is no Krylov subspace method for general matrices, which is given by a short recurrence relation and yet minimizes the norms of the residuals, as GMRES does.Another class of methods builds on the unsymmetric Lanczos iteration, in particular the BiCG method
Biconjugate gradient method
In mathematics, more specifically in numerical linear algebra, the biconjugate gradient method is an algorithm to solve systems of linear equationsA x= b.\,...
. These use a three-term recurrence relation, but they do not attain the minimum residual, and hence the residual does not decrease monotonically for these methods. Convergence is not even guaranteed.
The third class is formed by methods like CGS and BiCGSTAB
Biconjugate gradient stabilized method
In numerical linear algebra, the biconjugate gradient stabilized method, often abbreviated as BiCGSTAB, is an iterative method developed by H. A. van der Vorst for the numerical solution of nonsymmetric linear systems...
. These also work with a three-term recurrence relation (hence, without optimality) and they can even terminate prematurely without achieving convergence. The idea behind these methods is to choose the generating polynomials of the iteration sequence suitably.
None of these three classes is the best for all matrices; there are always examples in which one class outperforms the other. Therefore, multiple solvers are tried in practice to see which one is the best for a given problem.
Solving the least squares problem
One part of the GMRES method is to find the vector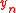 which minimizes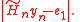Note that
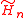is an (n+1)-by-n matrix, hence it gives an over-constrained linear system of n+1 equations for n unknowns.The minimum can be computed using a QR decomposition
QR decomposition
In linear algebra, a QR decomposition of a matrix is a decomposition of a matrix A into a product A=QR of an orthogonal matrix Q and an upper triangular matrix R...
: find an (n+1)-by-(n+1) orthogonal matrix
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
Ωn and an (n+1)-by-n upper triangular matrix
Triangular matrix
In the mathematical discipline of linear algebra, a triangular matrix is a special kind of square matrix where either all the entries below or all the entries above the main diagonal are zero...
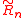such that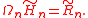The triangular matrix has one more row than it has columns, so its bottom row consists of zero. Hence, it can be decomposed as
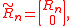
where
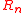is an n-by-n (thus square) triangular matrix.The QR decomposition can be updated cheaply from one iteration to the next, because the Hessenberg matrices differ only by a row of zeros and a column:
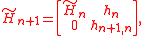
where hn = (h1n, … hnn)T. This implies that premultiplying the Hessenberg matrix with Ωn, augmented with zeroes and a row with multiplicative identity, yields almost a triangular matrix:
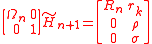
This would be triangular if σ is zero. To remedy this, one needs the Givens rotation
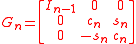
where
With this Givens rotation, we form
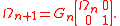
Indeed,
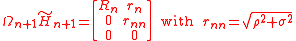
is a triangular matrix.
Given the QR decomposition, the minimization problem is easily solved by noting that
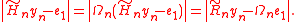
Denoting the vector
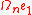by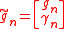with gn ∈ Rn and γn ∈ R, this is
The vector y that minimizes this expression is given by
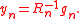
Again, the vectors
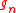are easy to update.