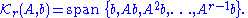Krylov subspace
Encyclopedia
In linear algebra
, the order-r Krylov subspace generated by an n-by-n matrix A and a vector b of dimension n is the linear subspace
spanned
by the images of b under the first r powers of A (starting from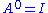
), that is,
It is named after Russian applied mathematician and naval engineer Alexei Krylov
, who published a paper on this issue in 1931.
Modern iterative method
s for finding one (or a few) eigenvalues of large sparse matrices
or solving large systems of linear equations avoid matrix-matrix operations, but rather multiply vectors by the matrix and work with the resulting vectors. Starting with a vector, b, one computes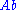
, then one multiplies that vector by A to find 
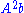and so on. All algorithms that work this way are referred to as Krylov subspace methods; they are among the most successful methods currently available in numerical linear algebra.
Because the vectors are linearly dependent
for powers of A greater than
, methods relying on Krylov subspace frequently involve some orthogonalization scheme, such as Lanczos iteration for Hermitian matrices or Arnoldi iteration
for more general matrices.
The best known Krylov subspace methods are the Arnoldi
, Lanczos, Conjugate gradient, GMRES (generalized minimum residual), BiCGSTAB (biconjugate gradient stabilized), QMR (quasi minimal residual), TFQMR (transpose-free QMR), and MINRES (minimal residual) methods.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, the order-r Krylov subspace generated by an n-by-n matrix A and a vector b of dimension n is the linear subspace
Linear subspace
The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
spanned
Linear span
In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
by the images of b under the first r powers of A (starting from
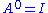), that is,
It is named after Russian applied mathematician and naval engineer Alexei Krylov
Alexei Krylov
Aleksey Nikolaevich Krylov was a Russian naval engineer, applied mathematician and memoirist.-Biography:Alexei Nikolaevich Krylov was born on August 3 O.S., 1863 to the family of an Army Artillery officer in a village Akhmatovo near town Alatyr of the Simbirsk Gubernia in Russia...
, who published a paper on this issue in 1931.
Modern iterative method
Iterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
s for finding one (or a few) eigenvalues of large sparse matrices
Sparse matrix
In the subfield of numerical analysis, a sparse matrix is a matrix populated primarily with zeros . The term itself was coined by Harry M. Markowitz....
or solving large systems of linear equations avoid matrix-matrix operations, but rather multiply vectors by the matrix and work with the resulting vectors. Starting with a vector, b, one computes
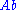, then one multiplies that vector by A to find 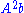and so on. All algorithms that work this way are referred to as Krylov subspace methods; they are among the most successful methods currently available in numerical linear algebra.Because the vectors are linearly dependent
Linear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
for powers of A greater than
, methods relying on Krylov subspace frequently involve some orthogonalization scheme, such as Lanczos iteration for Hermitian matrices or Arnoldi iterationArnoldi iteration
In numerical linear algebra, the Arnoldi iteration is an eigenvalue algorithm and an important example of iterative methods. Arnoldi finds the eigenvalues of general matrices; an analogous method for Hermitian matrices is the Lanczos iteration. The Arnoldi iteration was invented by W. E...
for more general matrices.
The best known Krylov subspace methods are the Arnoldi
Arnoldi iteration
In numerical linear algebra, the Arnoldi iteration is an eigenvalue algorithm and an important example of iterative methods. Arnoldi finds the eigenvalues of general matrices; an analogous method for Hermitian matrices is the Lanczos iteration. The Arnoldi iteration was invented by W. E...
, Lanczos, Conjugate gradient, GMRES (generalized minimum residual), BiCGSTAB (biconjugate gradient stabilized), QMR (quasi minimal residual), TFQMR (transpose-free QMR), and MINRES (minimal residual) methods.