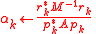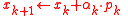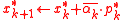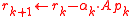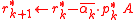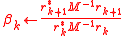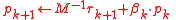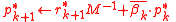Biconjugate gradient method
Encyclopedia
In mathematics
, more specifically in numerical linear algebra
, the biconjugate gradient method is an algorithm
to solve systems of linear equations
Unlike the conjugate gradient method
, this algorithm does not require the matrix
to be self-adjoint
, but instead one needs to perform multiplications by the conjugate transpose
.
In the above formulation, the computed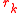
and 
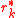satisfy
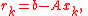
and thus are the respective residuals corresponding to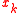
and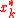 
, as approximate solutions to the systems
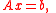
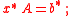
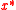is the adjoint
, and
is the complex conjugate
.
(compare to the biconjugate gradient stabilized method
), but very important from theoretical point of view. Define the iteration steps by
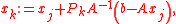
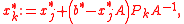
where
using the related projection
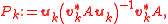
with
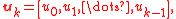
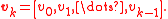
These related projections may be iterated themselves as
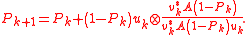
A relation to Quasi-Newton methods
is given by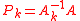
and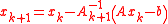 
, where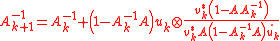
The new directions
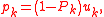
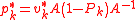
are then orthogonal to the residuals:
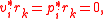
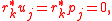
which themselves satisfy
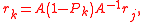
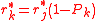
where
.
The biconjugate gradient method now makes a special choice and uses the setting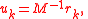
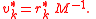
With this particular choice, explicit evaluations of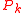
and are avoided, and the algorithm takes the form stated above.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more specifically in numerical linear algebra
Numerical linear algebra
Numerical linear algebra is the study of algorithms for performing linear algebra computations, most notably matrix operations, on computers. It is often a fundamental part of engineering and computational science problems, such as image and signal processing, Telecommunication, computational...
, the biconjugate gradient method is an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
to solve systems of linear equations
Unlike the conjugate gradient method
Conjugate gradient method
In mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is symmetric and positive-definite. The conjugate gradient method is an iterative method, so it can be applied to sparse systems that are too...
, this algorithm does not require the matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
to be self-adjointSelf-adjoint
In mathematics, an element x of a star-algebra is self-adjoint if x^*=x.A collection C of elements of a star-algebra is self-adjoint if it is closed under the involution operation...
, but instead one needs to perform multiplications by the conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
.
The algorithm
- Choose initial guess
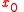, two other vectors 
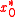and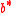 
and a preconditionerPreconditionerIn mathematics, preconditioning is a procedure of an application of a transformation, called the preconditioner, that conditions a given problem into a form that is more suitable for numerical solution. Preconditioning is typically related to reducing a condition number of the problem...
-
-
-
-
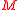
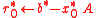
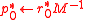
- for
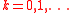do
-
In the above formulation, the computed
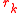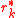and satisfy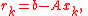and thus are the respective residuals corresponding to
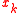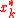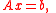
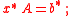
and , as approximate solutions to the systems 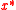is the adjointHermitian adjoint
In mathematics, specifically in functional analysis, each linear operator on a Hilbert space has a corresponding adjoint operator.Adjoints of operators generalize conjugate transposes of square matrices to infinite-dimensional situations...
, and
is the complex conjugateComplex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
.
Discussion
The biconjugate gradient method is numerically unstableNumerical stability
In the mathematical subfield of numerical analysis, numerical stability is a desirable property of numerical algorithms. The precise definition of stability depends on the context, but it is related to the accuracy of the algorithm....
(compare to the biconjugate gradient stabilized method
Biconjugate gradient stabilized method
In numerical linear algebra, the biconjugate gradient stabilized method, often abbreviated as BiCGSTAB, is an iterative method developed by H. A. van der Vorst for the numerical solution of nonsymmetric linear systems...
), but very important from theoretical point of view. Define the iteration steps by
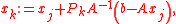
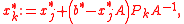
where
using the related projectionProjection (linear algebra)
In linear algebra and functional analysis, a projection is a linear transformation P from a vector space to itself such that P2 = P. It leaves its image unchanged....
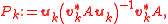
with
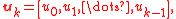
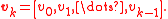
These related projections may be iterated themselves as
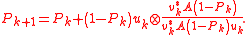
A relation to Quasi-Newton methods
Quasi-Newton method
In optimization, quasi-Newton methods are algorithms for finding local maxima and minima of functions. Quasi-Newton methods are based on...
is given by
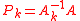and 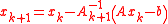, where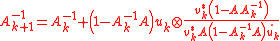The new directions
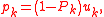
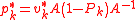
are then orthogonal to the residuals:
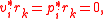
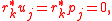
which themselves satisfy
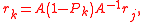
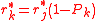
where
.The biconjugate gradient method now makes a special choice and uses the setting
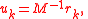
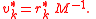
With this particular choice, explicit evaluations of
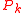and are avoided, and the algorithm takes the form stated above.Properties
- If
is self-adjointConjugate transposeIn mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
,
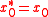and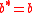 
, then 
, 
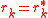, and the conjugate gradient methodConjugate gradient methodIn mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is symmetric and positive-definite. The conjugate gradient method is an iterative method, so it can be applied to sparse systems that are too...
produces the same sequence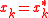
at half the computational cost.
- The sequences produced by the algorithm are biorthogonal, i.e.,
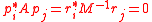for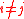 
.
- if
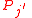is a polynomial with 
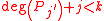, then 
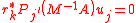. The algorithm thus produces projections onto the Krylov subspaceKrylov subspaceIn linear algebra, the order-r Krylov subspace generated by an n-by-n matrix A and a vector b of dimension n is the linear subspace spanned by the images of b under the first r powers of A , that is,...
.
- if
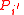is a polynomial with 
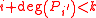, then 
.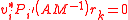