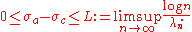General Dirichlet series
Encyclopedia
In the field of mathematical analysis
, a general Dirichlet series is an infinite series
that takes the form of
where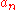
, 
are complex numbers
and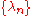
is a strictly increasing sequence
of positive numbers tends to infinity (1).
A simple observation shows that an 'ordinary' Dirichlet series
is obtained by substituting
n while a power series
is obtained when
.
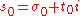, then it is uniformly convergent in the domain
and convergent for any
where 
.
There are now three possibilities regarding the convergence of a Dirichlet series, i.e. it may converge for all, for none or for some values of s. In the latter case, there exist a
such that the series is convergent for 
and divergent
for
. By convention, 
if the series converges nowhere and 
if the series converges everywhere on the complex plane
.
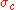above. Another equivalent definition is
The line
is called the line of convergence. The half-plane of convergence is defined as
The abscissa
, line
and half-plane
of convergence of a Dirichlet series are analogous to radius
, boundary
and disk
of convergence of a power series.
On the line of convergence, the question of convergence remains open as in the case of power series. However, if a Dirichlet series converges and diverges at different points on the same vertical line, then this line must be the line of convergence. The proof is implicit in the definition of abscissa of convergence. An example would be the series
which converges at
i (alternating harmonic series
) and diverges at
(harmonic series
). Thus,
is the line of convergence.
Suppose that a Dirichlet series does not converge at
, then it is clear that 
and 
diverges. On the other hand, if a Dirichlet series converges at 
, then 
and 
converges. Thus, there are two formulas to compute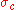 
, depending on the convergence of 
which can be determined by various convergence tests
. These formulas are similar to the Cauchy-Hadamard theorem for the radius of convergence of a power series.
If
is divergent, i.e. 
, then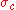 
is given by
If
is convergent, i.e. 
, then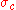 
is given by
if the series
is convergent. As usual, an absolutely convergent Dirichlet series is convergent, but the converse is not always true.
If a Dirichlet series is absolutely convergent at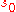
, then it is absolutely convergent for all s where 
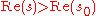. A Dirichlet series may converge absolutely for all, for no or for some values of s. In the latter case, there exist a 
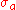such that the series converges absolutely for 
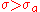and converges non-absolutely for 
.
The abscissa of absolute convergence can be defined as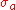
above, or equivalently as
The line and half-plane of absolute convergence can be defined similarly. There are also two formulas to compute
.
If
is divergent, then 
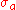is given by
If
is convergent, then 
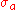is given by
In general, the abscissa of convergence does not coincide with abscissa of absolute convergence. Thus, there might be a strip between the line of convergence and absolute convergence where a Dirichlet series is conditionally convergent. The width of this strip is given by
In the case where L= 0, then
All the formulas provided so far still hold true for 'ordinary' Dirichlet series by substituting
n.
represented by a Dirichlet series
is analytic
on the half-plane of convergence. Moreover, for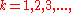
case where
, k = 2, 3, 4,..., or complex variable
case where
, m = 1, 2, 3,...
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, a general Dirichlet series is an infinite series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
that takes the form of
where
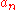, are complex numbersComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
and
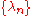is a strictly increasing sequenceSequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of positive numbers tends to infinity (1).
A simple observation shows that an 'ordinary' Dirichlet series
is obtained by substituting
n while a power series
is obtained when
.Fundamental theorems
If a Dirichlet series is convergent at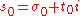, then it is uniformly convergent in the domain
and convergent for any
where .There are now three possibilities regarding the convergence of a Dirichlet series, i.e. it may converge for all, for none or for some values of s. In the latter case, there exist a
such that the series is convergent for and divergentDivergence (disambiguation)
Divergence can refer to:In mathematics:*Divergence, a function that associates a scalar with every point of a vector field*Divergence , a computation which does not terminate...
for
. By convention, if the series converges nowhere and if the series converges everywhere on the complex planeComplex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
.
Abscissa of convergence
The abscissa of convergence of a Dirichlet series can be defined as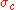 above. Another equivalent definition is-
converges for any s where Re(s)>
.
The line
is called the line of convergence. The half-plane of convergence is defined as
The abscissa
Abscissa
In mathematics, abscissa refers to that element of an ordered pair which is plotted on the horizontal axis of a two-dimensional Cartesian coordinate system, as opposed to the ordinate...
, line
Line
- Science and technology :* Line , a circuit or loop.** A power line for electric power transmission** line power or lines power, domestic mains electricity.** telephone line** RF transmission line...
and half-plane
Half-space
In geometry, a half-space is either of the two parts into which a plane divides the three-dimensional euclidean space. More generally, a half-space is either of the two parts into which a hyperplane divides an affine space...
of convergence of a Dirichlet series are analogous to radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
, boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
and disk
Disk (mathematics)
In geometry, a disk is the region in a plane bounded by a circle.A disk is said to be closed or open according to whether or not it contains the circle that constitutes its boundary...
of convergence of a power series.
On the line of convergence, the question of convergence remains open as in the case of power series. However, if a Dirichlet series converges and diverges at different points on the same vertical line, then this line must be the line of convergence. The proof is implicit in the definition of abscissa of convergence. An example would be the series
which converges at
i (alternating harmonic seriesHarmonic series (mathematics)
In mathematics, the harmonic series is the divergent infinite series:Its name derives from the concept of overtones, or harmonics in music: the wavelengths of the overtones of a vibrating string are 1/2, 1/3, 1/4, etc., of the string's fundamental wavelength...
) and diverges at
(harmonic seriesHarmonic series (mathematics)
In mathematics, the harmonic series is the divergent infinite series:Its name derives from the concept of overtones, or harmonics in music: the wavelengths of the overtones of a vibrating string are 1/2, 1/3, 1/4, etc., of the string's fundamental wavelength...
). Thus,
is the line of convergence.Suppose that a Dirichlet series does not converge at
, then it is clear that and diverges. On the other hand, if a Dirichlet series converges at , then and converges. Thus, there are two formulas to compute 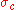, depending on the convergence of which can be determined by various convergence testsConvergence tests
In mathematics, convergence tests are methods of testing for the convergence, conditional convergence, absolute convergence, interval of convergence or divergence of an infinite series.- List of tests :...
. These formulas are similar to the Cauchy-Hadamard theorem for the radius of convergence of a power series.
If
is divergent, i.e. , then 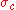is given by
If
is convergent, i.e. , then 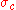is given by
Abscissa of absolute convergence
A Dirichlet series is absolutely convergentAbsolute convergence
In mathematics, a series of numbers is said to converge absolutely if the sum of the absolute value of the summand or integrand is finite...
if the series
is convergent. As usual, an absolutely convergent Dirichlet series is convergent, but the converse is not always true.
If a Dirichlet series is absolutely convergent at
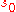, then it is absolutely convergent for all s where 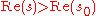. A Dirichlet series may converge absolutely for all, for no or for some values of s. In the latter case, there exist a 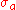such that the series converges absolutely for 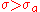and converges non-absolutely for .The abscissa of absolute convergence can be defined as
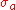above, or equivalently as-
converges absolutely for any s where Re(s)>
.
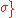The line and half-plane of absolute convergence can be defined similarly. There are also two formulas to compute
.If
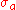is divergent, then is given by
If
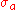is convergent, then is given by
In general, the abscissa of convergence does not coincide with abscissa of absolute convergence. Thus, there might be a strip between the line of convergence and absolute convergence where a Dirichlet series is conditionally convergent. The width of this strip is given by
In the case where L= 0, then
All the formulas provided so far still hold true for 'ordinary' Dirichlet series by substituting
n.Analytic functions
A functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
represented by a Dirichlet series
is analytic
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
on the half-plane of convergence. Moreover, for
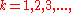
Further generalizations
A Dirichlet series can be further generalized to multi-variablesVariable
Variable may refer to:* Variable , a logical set of attributes* Variable , a symbol that represents a quantity in an algebraic expression....
case where
, k = 2, 3, 4,..., or complex variableComplex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
case where
, m = 1, 2, 3,...