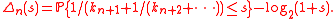Selected results

• 1n 1928, Kuzmin solved the following problem due to Gauss
  Carl Friedrich Gauss
  Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
  
   (see Gauss–Kuzmin distribution): if x is a random number chosen uniformly in (0, 1), and

is its continued fraction

Continued fraction

In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...

 expansion, find a bound for

Gauss showed that Δ_n tends to zero as n goes to infinity, however, he was unable to give an explicit bound. Kuzmin showed that

where C,α > 0 are numerical constants. In 1929, the bound was improved to C 0.7ⁿ by Paul Pierre Lévy

Paul Pierre Lévy

Paul Pierre Lévy was a Jewish French mathematician who was active especially in probability theory, introducing martingales and Lévy flights...

.

• In 1930, Kuzmin proved that numbers of the form a^b, where a is algebraic
  Algebraic number
  In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
  
   and b is a real quadratic irrational
  Quadratic irrational
  In mathematics, a quadratic irrational is an irrational number that is the solution to some quadratic equation with rational coefficients...
  
  , are transcendental
  Transcendental number
  In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
  
  . For example,

is transcendental. See Gelfond–Schneider theorem

Gelfond–Schneider theorem

In mathematics, the Gelfond–Schneider theorem establishes the transcendence of a large class of numbers. It was originally proved independently in 1934 by Aleksandr Gelfond and Theodor Schneider...

for later developments.