
Gallery of named graphs
Encyclopedia
Some of the finite structures considered in graph theory
have names, sometimes inspired by the graph's topology, and sometimes after their discoverer. A famous example is the Petersen graph
, a concrete graph on 10 vertices that appears as a minimal example or counterexample in many different contexts.
on v vertices and rank k is usually denoted srg(v,k,λ,μ).
is one in which there is a symmetry (graph automorphism
) taking any ordered pair of adjacent vertices to any other ordered pair; the Foster census lists all small symmetric 3-regular graphs. Every strongly regular graph is symmetric, but not vice versa.
on vertices is often called the
vertices is often called the  -clique and usually denoted
-clique and usually denoted 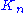 , from German komplett.
, from German komplett.
is usually denoted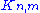 . The graph
. The graph 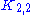 equals the 4-cycle
equals the 4-cycle 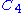 (the square) introduced below.
(the square) introduced below.
on vertices is called the n-cycle and usually denoted
vertices is called the n-cycle and usually denoted 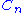 . It is also called a cyclic graph, a polygon or the n-gon. Special cases are the triangle
. It is also called a cyclic graph, a polygon or the n-gon. Special cases are the triangle 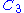 , the square
, the square 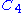 , and then several with Greek naming pentagon
, and then several with Greek naming pentagon 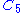 , hexagon
, hexagon 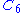 , etc.
, etc.
Fn can be constructed by joining n copies of the cycle graph
C3 with a common vertex.
refers to any 3-regular
, planar graph
with all faces of size 5 or 6 (including the external face). It follows from Euler's polyhedron formula
, V – E + F = 2 (where V, E, F indicate the number of vertices, edges, and faces), that there are exactly 12 pentagons in a fullerene and V/2–10 hexagons. Fullerene graphs are the Schlegel representations of the corresponding fullerene compounds.
An algorithm to generate all the non-isomorphic fullerens with a given number of hexagonal faces has been developed by G. Brinkmann and A. Dress. G. Brinkmann also provided a freely available implementation, called fullgen.
on four vertices forms the skeleton of the tetrahedron
, and more generally the complete graphs form skeletons of simplices
. The hypercube graphs are also skeletons of higher dimensional regular polytope
s.
is a bridgeless cubic graph
that requires four colors in any edge coloring
. The smallest snark is the Petersen graph
, already listed above.
Sk is the complete bipartite graph
K1,k. The star S3 is called the claw graph.

Wn is a graph on n vertices constructed by connecting a single vertex to every vertex in an (n − 1)-cycle.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
have names, sometimes inspired by the graph's topology, and sometimes after their discoverer. A famous example is the Petersen graph
Petersen graph
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it...
, a concrete graph on 10 vertices that appears as a minimal example or counterexample in many different contexts.
Strongly regular graphs
The strongly regular graphStrongly regular graph
In graph theory, a discipline within mathematics, a strongly regular graph is defined as follows. Let G = be a regular graph with v vertices and degree k...
on v vertices and rank k is usually denoted srg(v,k,λ,μ).
Symmetric graphs
A symmetric graphSymmetric graph
In the mathematical field of graph theory, a graph G is symmetric if, given any two pairs of adjacent vertices u1—v1 and u2—v2 of G, there is an automorphismsuch that...
is one in which there is a symmetry (graph automorphism
Graph automorphism
In the mathematical field of graph theory, an automorphism of a graph is a form of symmetry in which the graph is mapped onto itself while preserving the edge–vertex connectivity....
) taking any ordered pair of adjacent vertices to any other ordered pair; the Foster census lists all small symmetric 3-regular graphs. Every strongly regular graph is symmetric, but not vice versa.
Complete graphs
The complete graphComplete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
on
 vertices is often called the
vertices is often called the  -clique and usually denoted
-clique and usually denoted 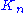 , from German komplett.
, from German komplett.Complete bipartite graphs
The complete bipartite graphComplete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
is usually denoted
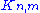 . The graph
. The graph 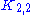 equals the 4-cycle
equals the 4-cycle 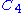 (the square) introduced below.
(the square) introduced below.Cycles
The cycle graphCycle graph
In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...
on
 vertices is called the n-cycle and usually denoted
vertices is called the n-cycle and usually denoted 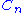 . It is also called a cyclic graph, a polygon or the n-gon. Special cases are the triangle
. It is also called a cyclic graph, a polygon or the n-gon. Special cases are the triangle 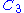 , the square
, the square 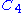 , and then several with Greek naming pentagon
, and then several with Greek naming pentagon 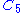 , hexagon
, hexagon 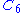 , etc.
, etc.Friendship graphs
The friendship graphFriendship graph
In the mathematical field of graph theory, the friendship graph Fn is a planar undirected graph with 2n+1 vertices and 3n edges....
Fn can be constructed by joining n copies of the cycle graph
Cycle graph
In graph theory, a cycle graph or circular graph is a graph that consists of a single cycle, or in other words, some number of vertices connected in a closed chain. The cycle graph with n vertices is called Cn...
C3 with a common vertex.
Fullerene graphs
In graph theory, the term fullereneFullerene
A fullerene is any molecule composed entirely of carbon, in the form of a hollow sphere, ellipsoid, or tube. Spherical fullerenes are also called buckyballs, and they resemble the balls used in association football. Cylindrical ones are called carbon nanotubes or buckytubes...
refers to any 3-regular
Regular graph
In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...
, planar graph
Planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
with all faces of size 5 or 6 (including the external face). It follows from Euler's polyhedron formula
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
, V – E + F = 2 (where V, E, F indicate the number of vertices, edges, and faces), that there are exactly 12 pentagons in a fullerene and V/2–10 hexagons. Fullerene graphs are the Schlegel representations of the corresponding fullerene compounds.
An algorithm to generate all the non-isomorphic fullerens with a given number of hexagonal faces has been developed by G. Brinkmann and A. Dress. G. Brinkmann also provided a freely available implementation, called fullgen.
Platonic solids
The complete graphComplete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
on four vertices forms the skeleton of the tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
, and more generally the complete graphs form skeletons of simplices
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
. The hypercube graphs are also skeletons of higher dimensional regular polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
s.
Snarks
A snarkSnark (graph theory)
In the mathematical field of graph theory, a snark is a connected, bridgeless cubic graph with chromatic index equal to 4. In other words, it is a graph in which every vertex has three neighbors, and the edges cannot be colored by only three colors without two edges of the same color meeting at a...
is a bridgeless cubic graph
Cubic graph
In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs....
that requires four colors in any edge coloring
Edge coloring
In graph theory, an edge coloring of a graph is an assignment of “colors” to the edges of the graph so that no two adjacent edges have the same color. For example, the figure to the right shows an edge coloring of a graph by the colors red, blue, and green. Edge colorings are one of several...
. The smallest snark is the Petersen graph
Petersen graph
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named for Julius Petersen, who in 1898 constructed it...
, already listed above.
Star
A starStar (graph theory)
In graph theory, a star Sk is the complete bipartite graph K1,k: a tree with one internal node and k leaves...
Sk is the complete bipartite graph
Complete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
K1,k. The star S3 is called the claw graph.

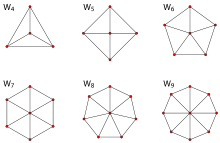
Wheel graphs
The wheel graphWheel graph
In the mathematical discipline of graph theory, a wheel graph Wn is a graph with n vertices, formed by connecting a single vertex to all vertices of an -cycle. The numerical notation for wheels is used inconsistently in the literature: some authors instead use n to refer to the length of the cycle,...
Wn is a graph on n vertices constructed by connecting a single vertex to every vertex in an (n − 1)-cycle.


