
Fundamental pair of periods
Encyclopedia
In mathematics
, a fundamental pair of periods is an ordered pair
of complex number
s that define a lattice
in the complex plane
. This type of lattice is the underlying object with which elliptic function
s and modular form
s are defined.
Although the concept of a two-dimensional lattice is quite simple, there is a considerable amount of specialized notation and language concerning the lattice that occurs in mathematical literature. This article attempts to review this notation, as well as to present some theorems that are specific to the two-dimensional case.

 such that their ratio
such that their ratio  is not real. In other words, considered as vectors in
is not real. In other words, considered as vectors in  , the two are not collinear. The lattice generated by
, the two are not collinear. The lattice generated by  and
and  is
is

This lattice is also sometimes denoted as to make clear that it depends on
to make clear that it depends on  and
and  . It is also sometimes denoted by
. It is also sometimes denoted by  or
or  , or simply by
, or simply by  . The two generators
. The two generators  and
and  are called the lattice basis.
are called the lattice basis.
The parallelogram
defined by the vertices 0, and
and  is called the fundamental parallelogram.
is called the fundamental parallelogram.
It is important to note that, while a fundamental pair generates a lattice, a lattice does not have any unique fundamental pair, that is, many (in fact, an infinite number) fundamental pairs correspond to the same lattice.
if they generate the same lattice: that is, if ⟨ω1,ω2⟩ = ⟨α1,α2⟩.
 and
and  are equivalent if and only if there exists a 2 × 2 matrix
are equivalent if and only if there exists a 2 × 2 matrix  with integer entries a, b, c and d and determinant
with integer entries a, b, c and d and determinant
ad − bc = ±1 such that

that is, so that

and

Note that this matrix belongs to the matrix group
 , which, with slight abuse of terminology, is known as the modular group
, which, with slight abuse of terminology, is known as the modular group
. This equivalence of lattices can be thought of as underlying many of the properties of elliptic function
s (especially the Weierstrass elliptic function) and modular forms.
 maps the complex plane into the fundamental parallelogram. That is, every point
maps the complex plane into the fundamental parallelogram. That is, every point  can be written as
can be written as  for integers m,n, with a point p in the fundamental parallelogram.
for integers m,n, with a point p in the fundamental parallelogram.
Since this mapping identifies opposite sides of the parallelogram as being the same, the fundamental parallelogram has the topology
of a torus
. Equivalently, one says that the quotient manifold is a torus.
is a torus.
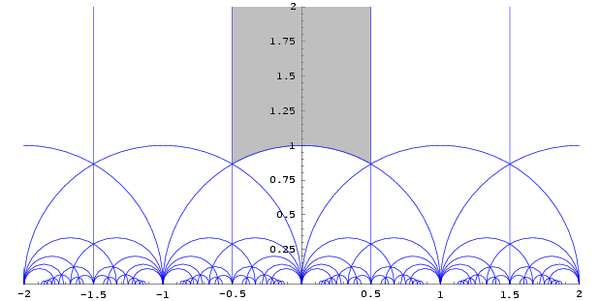 Define τ = ω2/ω1 to be the half-period ratio. Then the lattice basis can always be chosen so that τ lies in a special region,
Define τ = ω2/ω1 to be the half-period ratio. Then the lattice basis can always be chosen so that τ lies in a special region,
called the fundamental domain
. Alternately, there always exists an element of PSL(2,Z) that maps a lattice basis to another basis so that τ lies in the fundamental domain.
The fundamental domain is given by the set D, which is composed of a set U plus a part of the boundary of U:

where H is the upper half-plane.
The fundamental domain D is then built by adding the boundary on the left plus half the arc on the bottom:

If τ is not i and is not t=exp(1/3*pi*i), then there are exactly two lattice bases with the same τ in the fundamental region:
namely, and
and  . If
. If  then four lattice bases have the same τ: the above two and
then four lattice bases have the same τ: the above two and  . If t=exp(1/3*pi*i) then there are six lattice bases with the same τ:
. If t=exp(1/3*pi*i) then there are six lattice bases with the same τ:  ,
,  ,
,  and their negatives. Note that
and their negatives. Note that  and t=exp(1/3*pi*i) in the closure of the fundamental domain.
and t=exp(1/3*pi*i) in the closure of the fundamental domain.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a fundamental pair of periods is an ordered pair
Ordered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
of complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s that define a lattice
Lattice (group)
In mathematics, especially in geometry and group theory, a lattice in Rn is a discrete subgroup of Rn which spans the real vector space Rn. Every lattice in Rn can be generated from a basis for the vector space by forming all linear combinations with integer coefficients...
in the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
. This type of lattice is the underlying object with which elliptic function
Elliptic function
In complex analysis, an elliptic function is a function defined on the complex plane that is periodic in two directions and at the same time is meromorphic...
s and modular form
Modular form
In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
s are defined.
Although the concept of a two-dimensional lattice is quite simple, there is a considerable amount of specialized notation and language concerning the lattice that occurs in mathematical literature. This article attempts to review this notation, as well as to present some theorems that are specific to the two-dimensional case.

Definition
The fundamental pair of periods is a pair of complex numbers such that their ratio
such that their ratio  is not real. In other words, considered as vectors in
is not real. In other words, considered as vectors in  , the two are not collinear. The lattice generated by
, the two are not collinear. The lattice generated by  and
and  is
is
This lattice is also sometimes denoted as
 to make clear that it depends on
to make clear that it depends on  and
and  . It is also sometimes denoted by
. It is also sometimes denoted by  or
or  , or simply by
, or simply by  . The two generators
. The two generators  and
and  are called the lattice basis.
are called the lattice basis.The parallelogram
Parallelogram
In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...
defined by the vertices 0,
 and
and  is called the fundamental parallelogram.
is called the fundamental parallelogram.It is important to note that, while a fundamental pair generates a lattice, a lattice does not have any unique fundamental pair, that is, many (in fact, an infinite number) fundamental pairs correspond to the same lattice.
Equivalence
Two pairs of complex numbers (ω1,ω2) and (α1,α2) are called equivalentEquivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
if they generate the same lattice: that is, if ⟨ω1,ω2⟩ = ⟨α1,α2⟩.
No interior points
The fundamental parallelogram contains no further lattice points in its interior or boundary. Conversely, any pair of lattice points with this property constitute a fundamental pair, and furthermore, they generate the same lattice.Modular symmetry
Two pairs and
and  are equivalent if and only if there exists a 2 × 2 matrix
are equivalent if and only if there exists a 2 × 2 matrix  with integer entries a, b, c and d and determinant
with integer entries a, b, c and d and determinantDeterminant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
ad − bc = ±1 such that

that is, so that

and

Note that this matrix belongs to the matrix group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
 , which, with slight abuse of terminology, is known as the modular group
, which, with slight abuse of terminology, is known as the modular groupModular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
. This equivalence of lattices can be thought of as underlying many of the properties of elliptic function
Elliptic function
In complex analysis, an elliptic function is a function defined on the complex plane that is periodic in two directions and at the same time is meromorphic...
s (especially the Weierstrass elliptic function) and modular forms.
Topological properties
The abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
 maps the complex plane into the fundamental parallelogram. That is, every point
maps the complex plane into the fundamental parallelogram. That is, every point  can be written as
can be written as  for integers m,n, with a point p in the fundamental parallelogram.
for integers m,n, with a point p in the fundamental parallelogram.Since this mapping identifies opposite sides of the parallelogram as being the same, the fundamental parallelogram has the topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
of a torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
. Equivalently, one says that the quotient manifold
 is a torus.
is a torus.Fundamental region

called the fundamental domain
Fundamental domain
In geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group...
. Alternately, there always exists an element of PSL(2,Z) that maps a lattice basis to another basis so that τ lies in the fundamental domain.
The fundamental domain is given by the set D, which is composed of a set U plus a part of the boundary of U:

where H is the upper half-plane.
The fundamental domain D is then built by adding the boundary on the left plus half the arc on the bottom:

If τ is not i and is not t=exp(1/3*pi*i), then there are exactly two lattice bases with the same τ in the fundamental region:
namely,
 and
and  . If
. If  then four lattice bases have the same τ: the above two and
then four lattice bases have the same τ: the above two and  . If t=exp(1/3*pi*i) then there are six lattice bases with the same τ:
. If t=exp(1/3*pi*i) then there are six lattice bases with the same τ:  ,
,  ,
,  and their negatives. Note that
and their negatives. Note that  and t=exp(1/3*pi*i) in the closure of the fundamental domain.
and t=exp(1/3*pi*i) in the closure of the fundamental domain.See also
- A number of alternative notations for the lattice and for the fundamental pair exist, and are often used in its place. See, for example, the articles on the nome, elliptic modulus, quarter period and half-period ratio.
- Elliptic curveElliptic curveIn mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
- Modular formModular formIn mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
- Eisenstein seriesEisenstein seriesEisenstein series, named after German mathematician Gotthold Eisenstein, are particular modular forms with infinite series expansions that may be written down directly...

