.gif)
Fork (topology)
Encyclopedia
The notion of a fork appears in the characterization of graph
s, including network topology
, and topological space
s.
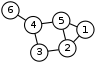A graph has a fork in any vertex
which is connected by three or more edges
. Correspondingly, a topological space is said to have a fork if it has a subset
which is homeomorphic to the graph topology of a graph with a fork.
Stated in terms of topology
alone, a topological space X has a fork if X has a closed
subset
T with connected
interior
, whose boundary
consists of three distinct elements and for which the boundary of the complement
of T 's interior (relative to X) consists of these same three elements.
It is perhaps worth noting that certain definitions of a simple curve as map
c : I → X of a real valued
interval
I to a topological space X such that c is continuous and injective (with the exception, for closed curves, of the two interval endpoints) are weaker than the requirement that its range X be a connected topological space without forks.
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
s, including network topology
Network topology
Network topology is the layout pattern of interconnections of the various elements of a computer or biological network....
, and topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s.
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
which is connected by three or more edges
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
. Correspondingly, a topological space is said to have a fork if it has a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
which is homeomorphic to the graph topology of a graph with a fork.
Stated in terms of topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
alone, a topological space X has a fork if X has a closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
T with connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
interior
Interior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
, whose boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
consists of three distinct elements and for which the boundary of the complement
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of T 's interior (relative to X) consists of these same three elements.
It is perhaps worth noting that certain definitions of a simple curve as map
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
c : I → X of a real valued
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
interval
Interval
Interval may refer to:* Interval , a range of numbers * Interval measurements or interval variables in statistics is a level of measurement...
I to a topological space X such that c is continuous and injective (with the exception, for closed curves, of the two interval endpoints) are weaker than the requirement that its range X be a connected topological space without forks.