
Essential matrix
Encyclopedia
In computer vision
, the essential matrix is a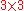 matrix
matrix
, , with some additional properties, which relates corresponding points in stereo images assuming that the cameras satisfy the pinhole camera model
, with some additional properties, which relates corresponding points in stereo images assuming that the cameras satisfy the pinhole camera model
.
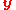 and
and 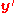 are homogeneous normalized image coordinates in image 1 and 2, respectively, then
are homogeneous normalized image coordinates in image 1 and 2, respectively, then

if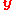 and
and 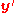 correspond to the same 3D point in the scene.
correspond to the same 3D point in the scene.
The above relation which defines the essential matrix was published in 1981 by Longuet-Higgins, introducing the concept to the computer vision community. Hartley & Zisserman's book reports that an analogous matrix appeared in photogrammetry
long before that. Longuet-Higgins' paper includes an algorithm for estimating from a set of corresponding normalized image coordinates as well as an algorithm for determining the relative position and orientation of the two cameras given that
from a set of corresponding normalized image coordinates as well as an algorithm for determining the relative position and orientation of the two cameras given that  is known. Finally, it shows how the 3D coordinates of the image points can be determined with the aid of the essential matrix.
is known. Finally, it shows how the 3D coordinates of the image points can be determined with the aid of the essential matrix.
Two normalized cameras project the 3D world onto their respective image planes. Let the 3D coordinates of a point P be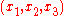 and
and 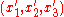 relative to each camera's coordinate system. Since the cameras are normalized, the corresponding image coordinates are
relative to each camera's coordinate system. Since the cameras are normalized, the corresponding image coordinates are
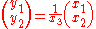 and
and 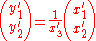
A homogeneous representation of the two image coordinates is then given by
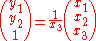 and
and 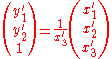
which also can be written more compactly as
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
, the essential matrix is a
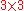 matrix
matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
,
 , with some additional properties, which relates corresponding points in stereo images assuming that the cameras satisfy the pinhole camera model
, with some additional properties, which relates corresponding points in stereo images assuming that the cameras satisfy the pinhole camera modelPinhole camera model
The pinhole camera model describes the mathematical relationship between the coordinates of a 3D point and its projection onto the image plane of an ideal pinhole camera, where the camera aperture is described as a point and no lenses are used to focus light...
.
Function
More specifically, if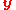 and
and 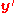 are homogeneous normalized image coordinates in image 1 and 2, respectively, then
are homogeneous normalized image coordinates in image 1 and 2, respectively, then
if
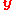 and
and 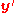 correspond to the same 3D point in the scene.
correspond to the same 3D point in the scene.The above relation which defines the essential matrix was published in 1981 by Longuet-Higgins, introducing the concept to the computer vision community. Hartley & Zisserman's book reports that an analogous matrix appeared in photogrammetry
Photogrammetry
Photogrammetry is the practice of determining the geometric properties of objects from photographic images. Photogrammetry is as old as modern photography and can be dated to the mid-nineteenth century....
long before that. Longuet-Higgins' paper includes an algorithm for estimating
 from a set of corresponding normalized image coordinates as well as an algorithm for determining the relative position and orientation of the two cameras given that
from a set of corresponding normalized image coordinates as well as an algorithm for determining the relative position and orientation of the two cameras given that  is known. Finally, it shows how the 3D coordinates of the image points can be determined with the aid of the essential matrix.
is known. Finally, it shows how the 3D coordinates of the image points can be determined with the aid of the essential matrix.Use
The essential matrix can be seen as a precursor to the fundamental matrix. Both matrices can be used for establishing constraints between matching image points, but the essential matrix can only be used in relation to calibrated cameras since the inner camera parameters must be known in order to achieve the normalization. If, however, the cameras are calibrated the essential matrix can be useful for determining both the relative position and orientation between the cameras and the 3D position of corresponding image points.Derivation and definition
This derivation follows the paper by Longuet-Higgins.Two normalized cameras project the 3D world onto their respective image planes. Let the 3D coordinates of a point P be
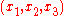 and
and 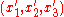 relative to each camera's coordinate system. Since the cameras are normalized, the corresponding image coordinates are
relative to each camera's coordinate system. Since the cameras are normalized, the corresponding image coordinates are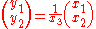 and
and 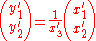
A homogeneous representation of the two image coordinates is then given by
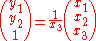 and
and 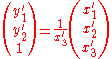
which also can be written more compactly as
-
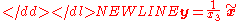 and
and 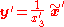
where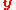 and
and 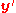 are homogeneous representations of the 2D image coordinates and
are homogeneous representations of the 2D image coordinates and 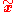 and
and 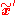 are proper 3D coordinates but in two different coordinate systems.
are proper 3D coordinates but in two different coordinate systems.
Another consequence of the normalized cameras is that their respective coordinate systems are related by means of a translation and rotation. This implies that the two sets of 3D coordinates are related as
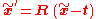
where is a
is a 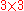 rotation matrix and
rotation matrix and  is a 3-dimensional translation vector.
is a 3-dimensional translation vector.
Define the essential matrix as
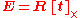
where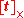 is the matrix representation of the cross product with
is the matrix representation of the cross product with  .
.
To see that this definition of the essential matrix describes a constraint on corresponding image coordinates multiply from left and right with the 3D coordinates of point P in the two different coordinate systems:
from left and right with the 3D coordinates of point P in the two different coordinate systems:
-
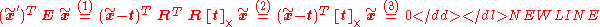
- Insert the above relations between
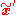 and
and 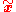 and the definition of
and the definition of  in terms of
in terms of  and
and  .
. -
 since
since  is a rotation matrix.
is a rotation matrix. - Properties of the matrix representation of the cross product.
Finally, it can be assumed that both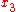 and
and 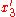 are > 0, otherwise they are not visible in both cameras. This gives
are > 0, otherwise they are not visible in both cameras. This gives
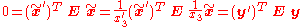
which is the constraint that the essential matrix defines between corresponding image points.
Properties of the essential matrix
Not every arbitrary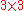 matrix can be an essential matrix for some stereo cameras. To see this notice that it is defined as the matrix product of one rotation matrix and one skew-symmetric matrixSkew-symmetric matrixIn mathematics, and in particular linear algebra, a skew-symmetric matrix is a square matrix A whose transpose is also its negative; that is, it satisfies the equation If the entry in the and is aij, i.e...
matrix can be an essential matrix for some stereo cameras. To see this notice that it is defined as the matrix product of one rotation matrix and one skew-symmetric matrixSkew-symmetric matrixIn mathematics, and in particular linear algebra, a skew-symmetric matrix is a square matrix A whose transpose is also its negative; that is, it satisfies the equation If the entry in the and is aij, i.e...
, both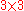 . The skew-symmetric matrix must have two singular values which are equal and another which is zero. The multiplication of the rotation matrix does not change the singular values which means that also the essential matrix has two singular values which are equal and one which is zero. The properties described here are sometimes referred to as internal constraints of the essential matrix.
. The skew-symmetric matrix must have two singular values which are equal and another which is zero. The multiplication of the rotation matrix does not change the singular values which means that also the essential matrix has two singular values which are equal and one which is zero. The properties described here are sometimes referred to as internal constraints of the essential matrix.
If the essential matrix is multiplied by a non-zero scalar, the result is again an essential matrix which defines exactly the same constraint as
is multiplied by a non-zero scalar, the result is again an essential matrix which defines exactly the same constraint as  does. This means that
does. This means that  can be seen as an element of a projective spaceProjective spaceIn mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
can be seen as an element of a projective spaceProjective spaceIn mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
, that is, two such matrices are considered equivalent if one is a non-zero scalar multiplication of the other. This is a relevant position, for example, if is estimated from image data. However, it is also possible to take the position that
is estimated from image data. However, it is also possible to take the position that  is defined as
is defined as
-

and then has a well-defined "scaling". It depends on the application which position is the more relevant.
has a well-defined "scaling". It depends on the application which position is the more relevant.
The constraints can also be expressed as-

and-
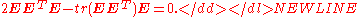
Here the last equation is matrix constraint, which can be seen as 9 constraints, one for each matrix element.
These constraints are often used for determining the essential matrix from five corresponding point pairs.
The essential matrix has five or six degrees of freedom, depending on whether or not it is seen as a projective element. The rotation matrix and the translation vector
and the translation vector  have three degrees of freedom each, in total six. If the essential matrix is considered as a projective element, however, one degree of freedom related to scalar multiplication must be subtracted leaving five degrees of freedom in total.
have three degrees of freedom each, in total six. If the essential matrix is considered as a projective element, however, one degree of freedom related to scalar multiplication must be subtracted leaving five degrees of freedom in total.
Estimation of the essential matrix
Given a set of corresponding image points it is possible to estimate an essential matrix which satisfies the defining epipolar constraint for all the points in the set. However, if the image points are subject to noise, which is the common case in any practical situation, it is not possible to find an essential matrix which satisfies all constraints exactly.
Depending on how the error related to each constraint is measured, it is possible to determine or estimate an essential matrix which optimally satisfies the constraints for a given set of corresponding image points. The most straight-forward approach is to set up a total least squares problem, commonly known as the eight-point algorithmEight-point algorithmThe eight-point algorithm is an algorithm used in computer vision to estimate the essential matrix or the fundamental matrix related to a stereo camera pair from a set of corresponding image points. It was introduced by Christopher Longuet-Higgins in 1981 for the case of the essential matrix...
.
Determining
Given that the essential matrix has been determined for a stereo camera pair, for example, using the estimation method above this information can be used for determining also the rotation and translation (up to a scaling) between the two camera's coordinate systems. In these derivations and
and  from
from 
 is seen as a projective element rather than having a well-determined scaling.
is seen as a projective element rather than having a well-determined scaling.
The following method for determining and
and  is based on performing a SVDSingular value decompositionIn linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
is based on performing a SVDSingular value decompositionIn linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
of , see Hartley & Zisserman's book. It is also possible to determine
, see Hartley & Zisserman's book. It is also possible to determine  and
and  without an SVD, for example, following Longuet-Higgins' paper.
without an SVD, for example, following Longuet-Higgins' paper.
Finding one solution
An SVD of gives
gives
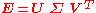
where and
and  are orthogonal
are orthogonal  matrices and
matrices and  is a
is a  diagonal matrix with
diagonal matrix with
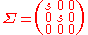
The diagonal entries of are the singular values of
are the singular values of  which, according to the internal constraints of the essential matrix, must consist of two identical and one zero value. Define
which, according to the internal constraints of the essential matrix, must consist of two identical and one zero value. Define
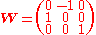 with
with 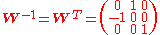
and make the following ansatzAnsatzAnsatz is a German noun with several meanings in the English language.It is widely encountered in physics and mathematics literature.Since ansatz is a noun, in German texts the initial a of this word is always capitalised.-Definition:...
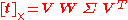

Since may not completely fulfill the constraints when dealing with real world data (f.e. camera images), the alternative
may not completely fulfill the constraints when dealing with real world data (f.e. camera images), the alternative
 with
with 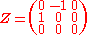
may help.
Showing that it is valid
First, these expressions for and
and 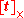 do satisfy the defining equation for the essential matrix
do satisfy the defining equation for the essential matrix

Second, it must be shown that this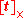 is a matrix representation of the cross product for some
is a matrix representation of the cross product for some  . Since
. Since
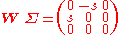
it is the case that is skew-symmetric, i.e.,
is skew-symmetric, i.e., 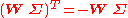 . This is also the case for our
. This is also the case for our 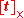 , since
, since
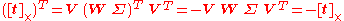
According to the general properties of the matrix representation of the cross product it then follows that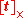 must be the cross product operator of exactly one vector
must be the cross product operator of exactly one vector  .
.
Third, it must also need to be shown that the above expression for is a rotation matrix. It is the product of three matrices which all are orthogonal which means that
is a rotation matrix. It is the product of three matrices which all are orthogonal which means that  , too, is orthogonal or
, too, is orthogonal or 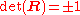 . To be a proper rotation matrix it must also satisfy
. To be a proper rotation matrix it must also satisfy  . Since, in this case,
. Since, in this case,  is seen as a projective element this can be accomplished by reversing the sign of
is seen as a projective element this can be accomplished by reversing the sign of  if necessary.
if necessary.
Finding all solutions
So far one possible solution for and
and  has been established given
has been established given  . It is, however, not the only possible solution and it may not even be a valid solution from a practical point of view. To begin with, since the scaling of
. It is, however, not the only possible solution and it may not even be a valid solution from a practical point of view. To begin with, since the scaling of  is undefined, the scaling of
is undefined, the scaling of  is also undefined. It must be lie in the null space of
is also undefined. It must be lie in the null space of  since
since
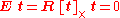
For the subsequent analysis of the solutions, however, the exact scaling of is not so important as its "sign", i.e., in which direction it points. Let
is not so important as its "sign", i.e., in which direction it points. Let 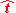 be normalized vector in the null space of
be normalized vector in the null space of  . It is then the case that both
. It is then the case that both 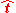 and
and 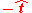 are valid translation vectors relative
are valid translation vectors relative  . It is also possible to change
. It is also possible to change  into
into 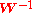 in the derivations of
in the derivations of  and
and  above. For the translation vector this only causes a change of sign, which has already been described as a possibility. For the rotation, on the other hand, this will produce a different transformation, at least in the general case.
above. For the translation vector this only causes a change of sign, which has already been described as a possibility. For the rotation, on the other hand, this will produce a different transformation, at least in the general case.
To summarize, given there are two opposite directions which are possible for
there are two opposite directions which are possible for  and two different rotations which are compatible with this essential matrix. In total this gives four classes of solutions for the rotation and translation between the two camera coordinate systems. On top of that, there is also an unknown scaling
and two different rotations which are compatible with this essential matrix. In total this gives four classes of solutions for the rotation and translation between the two camera coordinate systems. On top of that, there is also an unknown scaling  for the chosen translation direction.
for the chosen translation direction.
It turns out, however, that only one of the four classes of solutions can be realized in practice. Given a pair of corresponding image coordinates, three of the solutions will always produce a 3D point which lies behind at least one of the two cameras and therefore cannot be seen. Only one of the four classes will consistently produce 3D points which are in front of both cameras. This must then be the correct solution. Still, however, it has an undetermined positive scaling related to the translation component.
It should be noted that the above determination of and
and  assumes that
assumes that  satisfy the internal constraints of the essential matrix. If this is not the case which, for example, typically is the case if
satisfy the internal constraints of the essential matrix. If this is not the case which, for example, typically is the case if  has been estimated from real (and noisy) image data, it has to be assumed that it approximately satisfy the internal constraints. The vector
has been estimated from real (and noisy) image data, it has to be assumed that it approximately satisfy the internal constraints. The vector 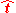 is then chosen as right singular vector of
is then chosen as right singular vector of  corresponding to the smallest singular value.
corresponding to the smallest singular value.
3D points from corresponding image points
The problem to be solved there is how to compute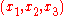 given corresponding normalized image coordinates
given corresponding normalized image coordinates 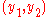 and
and 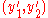 . If the essential matrix is known and the corresponding rotation and translation transformations have been determined, this algorithm (described in Longuet-Higgins' paper) provides a solution.
. If the essential matrix is known and the corresponding rotation and translation transformations have been determined, this algorithm (described in Longuet-Higgins' paper) provides a solution.
Let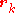 denote row k of the rotation matrix
denote row k of the rotation matrix  :
:
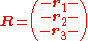
Combining the above relations between 3D coordinates in the two coordinate systems and the mapping between 3D and 2D points described earlier gives
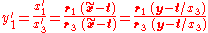
or
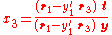
Once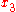 is determined, the other two coordinates can be computed as
is determined, the other two coordinates can be computed as
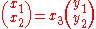
The above derivation is not unique. It is also possible to start with an expression for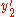 and derive an expression for
and derive an expression for 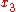 according to
according to
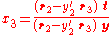
In the ideal case, when the camera maps the 3D points according to a perfect pinhole camera and the resulting 2D points can be detected without any noise, the two expressions for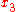 are equal. In practice, however, they are not and it may be advantageous to combine the two estimates of
are equal. In practice, however, they are not and it may be advantageous to combine the two estimates of 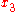 , for example, in terms of some sort of average.
, for example, in terms of some sort of average.
There are also other types of extensions of the above computations which are possible. They started with an expression of the primed image coordinates and derived 3D coordinates in the unprimed system. It is also possible to start with unprimed image coordinates and obtain primed 3D coordinates, which finally can be transformed into unprimed 3D coordinates. Again, in the ideal case the result should be equal to the above expressions, but in practice they may deviate.
A final remark relates to the fact that if the essential matrix is determined from corresponding image coordinate, which often is the case when 3D points are determined in this way, the translation vector is known only up to an unknown positive scaling. As a consequence, the reconstructed 3D points, too, are undetermined with respect to a positive scaling.
is known only up to an unknown positive scaling. As a consequence, the reconstructed 3D points, too, are undetermined with respect to a positive scaling.
-
-
- Insert the above relations between
-

