
Eight-point algorithm
Encyclopedia
The eight-point algorithm is an algorithm used in computer vision
to estimate the essential matrix or the fundamental matrix related to a stereo camera pair from a set of corresponding image points. It was introduced by Christopher Longuet-Higgins in 1981 for the case of the essential matrix. In theory, this algorithm can be used also for the fundamental matrix, but in practice the normalized eight-point algorithm, described by Richard Hartley in 1997, is better suited for this case.
The algorithm's name derives from the fact that it estimates the essential matrix or the fundamental matrix from a set of eight (or more) corresponding image points. However, variations of the algorithm can be used for fewer than eight points.
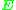 . It consists of three steps. First, it formulates a homogeneous linear equation, where the solution is directly related to
. It consists of three steps. First, it formulates a homogeneous linear equation, where the solution is directly related to 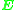 , and then solves the equation, taking into account that it may not have an exact solution. Finally, the internal constraints of the resulting matrix are managed. The first step is described in Longuet-Higgins' paper, the second and third steps are standard approaches in estimation theory.
, and then solves the equation, taking into account that it may not have an exact solution. Finally, the internal constraints of the resulting matrix are managed. The first step is described in Longuet-Higgins' paper, the second and third steps are standard approaches in estimation theory.
The constraint defined by the essential matrix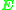 is
is
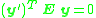
for corresponding image points represented in normalized image coordinates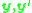 . The problem which the algorithm solves is to determine
. The problem which the algorithm solves is to determine 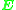 for a set of matching image points. In practice, the image coordinates of the image points are affected by noise and the solution may also be over-determined which means that it may not be possible to find
for a set of matching image points. In practice, the image coordinates of the image points are affected by noise and the solution may also be over-determined which means that it may not be possible to find  which satisfies the above constraint exactly for all points. This issue is addressed in the second step of the algorithm.
which satisfies the above constraint exactly for all points. This issue is addressed in the second step of the algorithm.
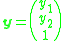 and
and 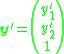 and
and 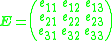
the constraint can also be rewritten as
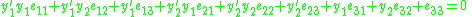
or
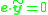
where
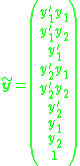 and
and 
that is, represents the essential matrix in the form of a 9-dimensional vector and this vector must be orthogonal to the vector
represents the essential matrix in the form of a 9-dimensional vector and this vector must be orthogonal to the vector 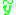 which can be seen as a vector representation of the
which can be seen as a vector representation of the  matrix
matrix 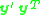 .
.
Each pair of corresponding image points produces a vector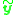 . Given a set of 3D points
. Given a set of 3D points 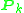 this corresponds to a set of vectors
this corresponds to a set of vectors 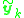 and all of them must satisfy
and all of them must satisfy
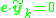
for the vector . Given sufficiently many (at least eight) linearly independent vectors
. Given sufficiently many (at least eight) linearly independent vectors  it is possible to determine
it is possible to determine  in a straightforward way. Collect all vectors
in a straightforward way. Collect all vectors 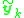 as the columns of a matrix
as the columns of a matrix  and it must then be the case that
and it must then be the case that
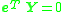
This means that is the solution to a homogeneous linear equation.
is the solution to a homogeneous linear equation.
 is a left singular vector
is a left singular vector
of corresponding to a singular value
corresponding to a singular value
that equals zero. Provided that at least eight linearly independent vectors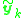 are used to construct
are used to construct 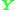 it follows that this singular vector is unique (disregarding scalar multiplication) and, consequently,
it follows that this singular vector is unique (disregarding scalar multiplication) and, consequently,  and then
and then 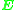 can be determined.
can be determined.
In the case that more than eight corresponding points are used to construct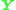 it is possible that it does not have any singular value equal to zero. This case occurs in practice when the image coordinates are affected by various types of noise. A common approach to deal with this situation is to describe it as a total least squares problem; find
it is possible that it does not have any singular value equal to zero. This case occurs in practice when the image coordinates are affected by various types of noise. A common approach to deal with this situation is to describe it as a total least squares problem; find  which minimizes
which minimizes
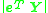
when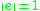 . The solution is to choose
. The solution is to choose  as the left singular vector corresponding to the smallest singular value of
as the left singular vector corresponding to the smallest singular value of 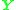 . A reordering of this
. A reordering of this  back into a
back into a 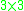 matrix gives the result of this step, here referred to as
matrix gives the result of this step, here referred to as 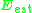 .
.
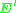 of rank 2 which minimizes
of rank 2 which minimizes
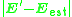
where is the resulting matrix from Step 2 and the Frobenius matrix norm is used. The solution to the problem is given by first computing a singular value decomposition of
is the resulting matrix from Step 2 and the Frobenius matrix norm is used. The solution to the problem is given by first computing a singular value decomposition of 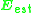 :
:
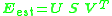
where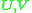 are orthogonal matrices and
are orthogonal matrices and 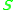 is a diagonal matrix which contains the singular values of
is a diagonal matrix which contains the singular values of 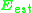 . In the ideal case, one of the diagonal elements of
. In the ideal case, one of the diagonal elements of 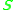 should be zero, or at least small compared to the other two which should be equal. In any case, set
should be zero, or at least small compared to the other two which should be equal. In any case, set
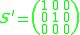
Finally, is given by
is given by
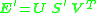
The matrix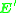 is the resulting estimate of the essential matrix provided by the algorithm.
is the resulting estimate of the essential matrix provided by the algorithm.
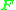 . The defining constraint for
. The defining constraint for 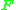 is
is
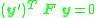
where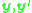 are the homogeneous representations of corresponding image coordinates (not necessary normalized). This means that it is possible to form a matrix
are the homogeneous representations of corresponding image coordinates (not necessary normalized). This means that it is possible to form a matrix 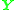 in a similar way as for the essential matrix and solve the equation
in a similar way as for the essential matrix and solve the equation
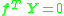
for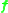 which is a reshaped version of
which is a reshaped version of  . By following the procedure outlined above, it is then possible to determine
. By following the procedure outlined above, it is then possible to determine 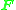 from a set of eight matching points. In practice, however, the resulting fundamental matrix may not be useful for determining epipolar constraints.
from a set of eight matching points. In practice, however, the resulting fundamental matrix may not be useful for determining epipolar constraints.
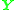 often is ill-conditioned. In theory,
often is ill-conditioned. In theory,  should have one singular value equal to zero and the rest are non-zero. In practice, however, some of the non-zero singular values can become small relative to the larger ones. If more than eight corresponding points are used to construct
should have one singular value equal to zero and the rest are non-zero. In practice, however, some of the non-zero singular values can become small relative to the larger ones. If more than eight corresponding points are used to construct 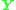 , where the coordinates are only approximately correct, there may not be a well-defined singular value which can be identified as approximately zero. Consequently, the solution of the homogeneous linear system of equations may not be sufficiently accurate to be useful.
, where the coordinates are only approximately correct, there may not be a well-defined singular value which can be identified as approximately zero. Consequently, the solution of the homogeneous linear system of equations may not be sufficiently accurate to be useful.
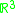 . A typical homogeneous representation of the 2D image coordinate
. A typical homogeneous representation of the 2D image coordinate 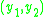 is
is
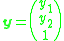
where both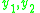 lie in the range 0 to 1000-2000 for a modern digital camera. This means that the first two coordinates in
lie in the range 0 to 1000-2000 for a modern digital camera. This means that the first two coordinates in 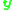 vary over a much larger range than the third coordinate. Furthermore, if the image points which are used to construct
vary over a much larger range than the third coordinate. Furthermore, if the image points which are used to construct 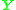 lie in a relatively small region of the image, for example at
lie in a relatively small region of the image, for example at 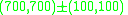 , again the vector
, again the vector 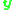 points in more or less the same direction for all points. As a consequence,
points in more or less the same direction for all points. As a consequence, 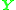 will have one large singular value and the remaining are small.
will have one large singular value and the remaining are small.
This principle results, normally, in a distinct coordinate transformation for each of the two images. As a result, new homogeneous image coordinates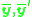 are given by
are given by


where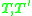 are the transformations (translation and scaling) from the old to the new normalized image coordinates. This normalization is only dependent on the image points which are used in a single image and is, in general, distinct from normalized image coordinates produced by a normalized camera.
are the transformations (translation and scaling) from the old to the new normalized image coordinates. This normalization is only dependent on the image points which are used in a single image and is, in general, distinct from normalized image coordinates produced by a normalized camera.
The epipolar constraint based on the fundamental matrix can now be rewritten as
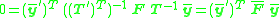
where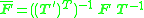 . This means that it is possible to use the normalized homogeneous image coordinates
. This means that it is possible to use the normalized homogeneous image coordinates  to estimate the transformed fundamental matrix
to estimate the transformed fundamental matrix 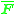 using the basic eight-point algorithm described above.
using the basic eight-point algorithm described above.
The purpose of the normalization transformations is that the matrix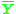 , constructed from the normalized image coordinates, in general has a better condition number than
, constructed from the normalized image coordinates, in general has a better condition number than 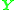 has. This means that the solution
has. This means that the solution 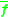 is more well-defined as a solution of the homogeneous equation
is more well-defined as a solution of the homogeneous equation 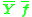 than
than 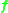 is relative to
is relative to  . Once
. Once  has been determined and reshaped into
has been determined and reshaped into 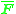 the latter can be de-normalized to give
the latter can be de-normalized to give 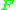 according to
according to
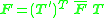
In general, this estimate of the fundamental matrix is a better one than would have been obtained by estimating from the un-normalized coordinates.
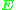 . Since
. Since 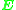 has five degrees of freedom it should therefore be sufficient with only five point pairs to determine
has five degrees of freedom it should therefore be sufficient with only five point pairs to determine 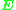 . Though possible from a theoretical point of view, the practical implementation of this is not straightforward and have to rely on solving various non-linear equations.
. Though possible from a theoretical point of view, the practical implementation of this is not straightforward and have to rely on solving various non-linear equations.
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
to estimate the essential matrix or the fundamental matrix related to a stereo camera pair from a set of corresponding image points. It was introduced by Christopher Longuet-Higgins in 1981 for the case of the essential matrix. In theory, this algorithm can be used also for the fundamental matrix, but in practice the normalized eight-point algorithm, described by Richard Hartley in 1997, is better suited for this case.
The algorithm's name derives from the fact that it estimates the essential matrix or the fundamental matrix from a set of eight (or more) corresponding image points. However, variations of the algorithm can be used for fewer than eight points.
The basic algorithm
The basic eight-point algorithm is here described for the case of estimating the essential matrix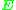 . It consists of three steps. First, it formulates a homogeneous linear equation, where the solution is directly related to
. It consists of three steps. First, it formulates a homogeneous linear equation, where the solution is directly related to 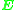 , and then solves the equation, taking into account that it may not have an exact solution. Finally, the internal constraints of the resulting matrix are managed. The first step is described in Longuet-Higgins' paper, the second and third steps are standard approaches in estimation theory.
, and then solves the equation, taking into account that it may not have an exact solution. Finally, the internal constraints of the resulting matrix are managed. The first step is described in Longuet-Higgins' paper, the second and third steps are standard approaches in estimation theory.The constraint defined by the essential matrix
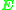 is
is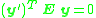
for corresponding image points represented in normalized image coordinates
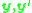 . The problem which the algorithm solves is to determine
. The problem which the algorithm solves is to determine 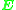 for a set of matching image points. In practice, the image coordinates of the image points are affected by noise and the solution may also be over-determined which means that it may not be possible to find
for a set of matching image points. In practice, the image coordinates of the image points are affected by noise and the solution may also be over-determined which means that it may not be possible to find  which satisfies the above constraint exactly for all points. This issue is addressed in the second step of the algorithm.
which satisfies the above constraint exactly for all points. This issue is addressed in the second step of the algorithm.Step 1: Formulating a homogeneous linear equation
With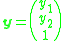 and
and 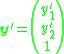 and
and 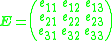
the constraint can also be rewritten as
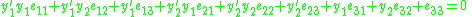
or
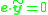
where
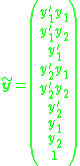 and
and 
that is,
 represents the essential matrix in the form of a 9-dimensional vector and this vector must be orthogonal to the vector
represents the essential matrix in the form of a 9-dimensional vector and this vector must be orthogonal to the vector 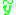 which can be seen as a vector representation of the
which can be seen as a vector representation of the  matrix
matrix 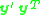 .
.Each pair of corresponding image points produces a vector
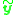 . Given a set of 3D points
. Given a set of 3D points 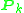 this corresponds to a set of vectors
this corresponds to a set of vectors 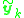 and all of them must satisfy
and all of them must satisfy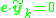
for the vector
 . Given sufficiently many (at least eight) linearly independent vectors
. Given sufficiently many (at least eight) linearly independent vectors  it is possible to determine
it is possible to determine  in a straightforward way. Collect all vectors
in a straightforward way. Collect all vectors 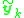 as the columns of a matrix
as the columns of a matrix  and it must then be the case that
and it must then be the case that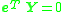
This means that
 is the solution to a homogeneous linear equation.
is the solution to a homogeneous linear equation.Step 2: Solving the equation
A standard approach to solving this equation implies that is a left singular vector
is a left singular vectorSingular value decomposition
In linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
of
 corresponding to a singular value
corresponding to a singular valueSingular value decomposition
In linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
that equals zero. Provided that at least eight linearly independent vectors
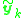 are used to construct
are used to construct 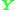 it follows that this singular vector is unique (disregarding scalar multiplication) and, consequently,
it follows that this singular vector is unique (disregarding scalar multiplication) and, consequently,  and then
and then 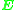 can be determined.
can be determined.In the case that more than eight corresponding points are used to construct
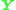 it is possible that it does not have any singular value equal to zero. This case occurs in practice when the image coordinates are affected by various types of noise. A common approach to deal with this situation is to describe it as a total least squares problem; find
it is possible that it does not have any singular value equal to zero. This case occurs in practice when the image coordinates are affected by various types of noise. A common approach to deal with this situation is to describe it as a total least squares problem; find  which minimizes
which minimizes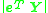
when
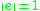 . The solution is to choose
. The solution is to choose  as the left singular vector corresponding to the smallest singular value of
as the left singular vector corresponding to the smallest singular value of 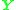 . A reordering of this
. A reordering of this  back into a
back into a 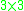 matrix gives the result of this step, here referred to as
matrix gives the result of this step, here referred to as 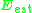 .
.Step 3: Enforcing the internal constraint
Another consequence of dealing with noisy image coordinates is that the resulting matrix may not satisfy the internal constraint of the essential matrix, that is, two of its singular values are equal and nonzero and the other is zero. Depending on the application, smaller or larger deviations from the internal constraint may or may not be a problem. If it is critical that the estimated matrix satisfies the internal constraints, this can be accomplished by finding the matrix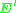 of rank 2 which minimizes
of rank 2 which minimizes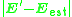
where
 is the resulting matrix from Step 2 and the Frobenius matrix norm is used. The solution to the problem is given by first computing a singular value decomposition of
is the resulting matrix from Step 2 and the Frobenius matrix norm is used. The solution to the problem is given by first computing a singular value decomposition of 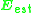 :
: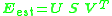
where
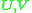 are orthogonal matrices and
are orthogonal matrices and 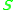 is a diagonal matrix which contains the singular values of
is a diagonal matrix which contains the singular values of 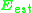 . In the ideal case, one of the diagonal elements of
. In the ideal case, one of the diagonal elements of 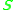 should be zero, or at least small compared to the other two which should be equal. In any case, set
should be zero, or at least small compared to the other two which should be equal. In any case, set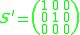
Finally,
 is given by
is given by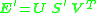
The matrix
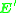 is the resulting estimate of the essential matrix provided by the algorithm.
is the resulting estimate of the essential matrix provided by the algorithm.The normalized eight-point algorithm
The basic eight-point algorithm can in principle be used also for estimating the fundamental matrix . The defining constraint for
. The defining constraint for 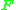 is
is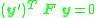
where
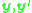 are the homogeneous representations of corresponding image coordinates (not necessary normalized). This means that it is possible to form a matrix
are the homogeneous representations of corresponding image coordinates (not necessary normalized). This means that it is possible to form a matrix 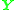 in a similar way as for the essential matrix and solve the equation
in a similar way as for the essential matrix and solve the equation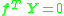
for
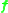 which is a reshaped version of
which is a reshaped version of  . By following the procedure outlined above, it is then possible to determine
. By following the procedure outlined above, it is then possible to determine 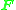 from a set of eight matching points. In practice, however, the resulting fundamental matrix may not be useful for determining epipolar constraints.
from a set of eight matching points. In practice, however, the resulting fundamental matrix may not be useful for determining epipolar constraints.The problem
The problem is that the resulting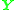 often is ill-conditioned. In theory,
often is ill-conditioned. In theory,  should have one singular value equal to zero and the rest are non-zero. In practice, however, some of the non-zero singular values can become small relative to the larger ones. If more than eight corresponding points are used to construct
should have one singular value equal to zero and the rest are non-zero. In practice, however, some of the non-zero singular values can become small relative to the larger ones. If more than eight corresponding points are used to construct  , where the coordinates are only approximately correct, there may not be a well-defined singular value which can be identified as approximately zero. Consequently, the solution of the homogeneous linear system of equations may not be sufficiently accurate to be useful.
, where the coordinates are only approximately correct, there may not be a well-defined singular value which can be identified as approximately zero. Consequently, the solution of the homogeneous linear system of equations may not be sufficiently accurate to be useful.What's causing the problem
Hartley addressed this estimation problem in his 1997 article. His analysis of the problem shows that the problem is caused by the poor distribution of the homogeneous image coordinates in their space,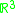 . A typical homogeneous representation of the 2D image coordinate
. A typical homogeneous representation of the 2D image coordinate 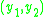 is
is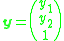
where both
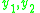 lie in the range 0 to 1000-2000 for a modern digital camera. This means that the first two coordinates in
lie in the range 0 to 1000-2000 for a modern digital camera. This means that the first two coordinates in 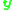 vary over a much larger range than the third coordinate. Furthermore, if the image points which are used to construct
vary over a much larger range than the third coordinate. Furthermore, if the image points which are used to construct 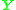 lie in a relatively small region of the image, for example at
lie in a relatively small region of the image, for example at 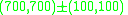 , again the vector
, again the vector 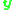 points in more or less the same direction for all points. As a consequence,
points in more or less the same direction for all points. As a consequence, 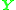 will have one large singular value and the remaining are small.
will have one large singular value and the remaining are small.How it can be solved
As a solution to this problem, Hartley proposed that the coordinate system of each of the two images should be transformed, independently, into a new coordinate system according to the following principle.- The origin of the new coordinate system should be centered (have its origin) at the centroid (center of gravity) of the image points. This is accomplished by a translation of the original origin to the new one.
- After the translation the coordinates are uniformly scaled so that the mean distance from the origin to a point equals
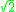 .
.
This principle results, normally, in a distinct coordinate transformation for each of the two images. As a result, new homogeneous image coordinates
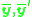 are given by
are given by

where
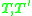 are the transformations (translation and scaling) from the old to the new normalized image coordinates. This normalization is only dependent on the image points which are used in a single image and is, in general, distinct from normalized image coordinates produced by a normalized camera.
are the transformations (translation and scaling) from the old to the new normalized image coordinates. This normalization is only dependent on the image points which are used in a single image and is, in general, distinct from normalized image coordinates produced by a normalized camera.The epipolar constraint based on the fundamental matrix can now be rewritten as
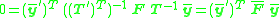
where
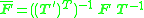 . This means that it is possible to use the normalized homogeneous image coordinates
. This means that it is possible to use the normalized homogeneous image coordinates  to estimate the transformed fundamental matrix
to estimate the transformed fundamental matrix 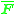 using the basic eight-point algorithm described above.
using the basic eight-point algorithm described above.The purpose of the normalization transformations is that the matrix
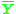 , constructed from the normalized image coordinates, in general has a better condition number than
, constructed from the normalized image coordinates, in general has a better condition number than 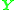 has. This means that the solution
has. This means that the solution 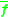 is more well-defined as a solution of the homogeneous equation
is more well-defined as a solution of the homogeneous equation 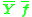 than
than 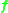 is relative to
is relative to  . Once
. Once  has been determined and reshaped into
has been determined and reshaped into 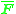 the latter can be de-normalized to give
the latter can be de-normalized to give 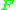 according to
according to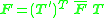
In general, this estimate of the fundamental matrix is a better one than would have been obtained by estimating from the un-normalized coordinates.
Using fewer than eight points
Each point pair contributes with one constraining equation on the element in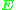 . Since
. Since 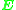 has five degrees of freedom it should therefore be sufficient with only five point pairs to determine
has five degrees of freedom it should therefore be sufficient with only five point pairs to determine 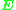 . Though possible from a theoretical point of view, the practical implementation of this is not straightforward and have to rely on solving various non-linear equations.
. Though possible from a theoretical point of view, the practical implementation of this is not straightforward and have to rely on solving various non-linear equations.

