
Erdos–Straus conjecture
Encyclopedia
In number theory
, the Erdős–Straus conjecture states that for all integer
s n ≥ 2, the rational number
4/n can be expressed as the sum of three unit fraction
s. Paul Erdős
and Ernst G. Straus
formulated the conjecture in 1948; It is one of many conjectures by Erdős
.
More formally, the conjecture states that, for every integer n ≥ 4, there exist positive integers x, y, and z such that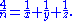
These unit fractions form an Egyptian fraction representation of the number 4/n. For instance, for n = 5, there are two solutions: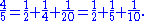
The restriction that x, y, and z be positive is essential to the difficulty of the problem, for if negative values were allowed the problem could be solved trivially. Also, if n is a composite number
, n = pq, then an expansion for 4/n could be found immediately from an expansion for 4/p or 4/q. Therefore, if a counterexample to the Erdős–Straus conjecture exists, the smallest n forming a counterexample would have to be a prime number
, and it can be further restricted to one of six arithmetic progression
s modulo 840. Computer searches have verified the truth of the conjecture up to n ≤ 1014, but proving it for all n remains an open problem.
, in which Egyptian fraction expansions of this type were used as a notation for recording fractional quantities. The Egyptians produced tables such as the Rhind Mathematical Papyrus 2/n table
of expansions of fractions of the form 2/n, most of which use either two or three terms.
The greedy algorithm for Egyptian fractions
, first described in 1202 by Fibonacci
in his book Liber Abaci
, finds an expansion in which each successive term is the largest unit fraction that is no larger than the remaining number to be represented. For fractions of the form 2/n or 3/n, the greedy algorithm uses at most two or three terms respectively. More generally, it can be shown that a number of the form 3/n has a two-term expansion if and only if n has a factor congruent to 2 modulo 3, and requires three terms in any expansion otherwise.
Thus, for the numerators 2 and 3, the question of how many terms are needed in an Egyptian fraction is completely settled, and fractions of the form 4/n are the first case in which the worst-case length of an expansion remains unknown. The greedy algorithm produces expansions of length two, three, or four depending on the value of n modulo 4; when n is congruent to 1 modulo 4, the greedy algorithm produces four-term expansions. Therefore, the worst-case length of an Egyptian fraction of 4/n must be either three or four. The Erdős–Straus conjecture states that, in this case, as in the case for the numerator 3, the maximum number of terms in an expansion is three.
. The Hasse principle
for Diophantine equations asserts that an integer solution of a Diophantine equation should be formed by combining solutions obtained modulo each possible prime number
. On the face of it this principle makes little sense for the Erdős–Straus conjecture, as the equation 4xyz = n(xy + xz + yz) is easily solvable modulo any prime. Nevertheless, modular identities have proven a very important tool in the study of the conjecture.
For values of n satisfying certain congruence relations
, one can find an expansion for 4/n automatically as an instance of a polynomial identity. For instance, whenever n ≡ 2 (mod 3),4/n has the expansion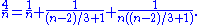
Here each of the three denominators n, (n − 2)/3 + 1, and n((n − 2)/3 + 1) is a polynomial of n, and each is an integer whenever n is 2 (mod 3).
The greedy algorithm for Egyptian fractions
finds a solution in three or fewer terms whenever n is not 1 or 17 (mod 24), and the n ≡ 17 (mod 24) case is covered by the 2 (mod 3) relation, so the only values of n for which these two methods do not find expansions in three or fewer terms are those congruent to 1 (mod 24).
If it were possible to find solutions such as the ones above for enough different moduli, forming a complete covering system of congruences, the problem would be solved. However, as showed, a polynomial identity that provides a solution for values of n congruent to r mod p can exist only when r is not a quadratic residue modulo p. For instance, 2 is a not a quadratic residue modulo 3, so the existence of an identity for values of n that are congruent to 2 modulo 3 does not contradict Mordell's result, but 1 is a quadratic residue modulo 3 so the result proves that there can be no similar identity for values of n that are congruent to 1 modulo 3.
Mordell lists polynomial identities that provide three-term Egyptian fractions for 4/n whenever n is 2 mod 3 (above), 3 mod 4, 5 mod 8, 2 or 3 mod 5, or 3, 5, or 6 mod 7. These identies cover all the numbers that are not quadratic residues for those bases. However, for larger bases, not all nonresidues are known to be covered by relations of this type. From Mordell's identities one can conclude that there exists a solution for all n except possibly those that are 1, 121, 169, 289, 361, or 529 modulo 840. 1009 is the smallest prime number that is not covered by this system of congruences. By combining larger classes of modular identities, Webb and others showed that the fraction of n in the interval [1,N] that can be counterexamples to the conjecture tends to zero in the limit as N goes to infinity.
Despite Mordell's result limiting the form these congruence identities can take, there is still some hope of using modular identities to prove the Erdős–Straus conjecture. No prime number can be a square, so by the Hasse-Minkowski theorem, whenever p is prime, there exists a larger prime q such that p is not a quadratic residue modulo q. One possible approach to proving the conjecture would be
to find for each prime p a larger prime q and a congruence solving the 4/n problem for n ≡ p (mod q); if this could be done, no prime p could be a counterexample to the conjecture and the conjecture would be true.
es for counterexamples to the conjecture; these searches can be greatly sped up by considering only prime numbers that are not covered by known congruence relations. Searches of this type by Allan Swett confirmed that the conjecture is true for all n up to 1014.
Even for larger n there can be relatively few solutions; for instance there are only seven distinct solutions for n = 73.
have shown that the average number of solutions to the 4/n problem (averaged over the prime numbers up to n) grows polylogarithmic
ally in n. For some other Diophantine problems, it is possible to prove that a solution always exists by proving asymptotic lower bounds on the number of solutions, but proofs of this type exist primarily for problems in which the number of solutions grows polynomially, so Tao's result makes a solution of this type less likely. The proof of Tao's bound on the number of solutions involves the Bombieri–Vinogradov theorem
, the Brun–Titchmarsh theorem
, and a system of modular identities, valid when n is congruent to −c or −1/c modulo 4ab, where a and b are any two coprime
positive integers and c is any odd factor of a + b. For instance, setting a = b = 1 gives one of Mordell's identities, valid when n is 3 (mod 4).
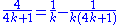
and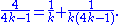
Alternatively, for any odd n, a three-term solution with one negative term is possible: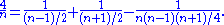
.
Even if the generalized conjecture is false for any fixed value of k, then the number of fractions k/n with n in the range from 1 to N that do not have three-term expansions must grow only sublinearly as a function of N. In particular, if the Erdős–Straus conjecture itself (the case k = 4) is false, then the number of counterexamples grows only sublinearly. Even more strongly, for any fixed k, only a sublinear number of values of n need more than two terms in their Egyptian fraction expansions. The generalized version of the conjecture is equivalent to the statement that the number of unexpandable fractions is not just sublinear but bounded.
When n is an odd number, by analogy to the problem of odd greedy expansions for Egyptian fractions, one may ask for solutions to k/n = 1/x + 1/y + 1/z in which x, y, and z are distinct positive odd numbers. Solutions to this equation are known to always exist for the case that k = 3.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the Erdős–Straus conjecture states that for all integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s n ≥ 2, the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
4/n can be expressed as the sum of three unit fraction
Unit fraction
A unit fraction is a rational number written as a fraction where the numerator is one and the denominator is a positive integer. A unit fraction is therefore the reciprocal of a positive integer, 1/n...
s. Paul Erdős
Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
and Ernst G. Straus
Ernst G. Straus
Ernst Gabor Straus was a German-American mathematician who helped found the theories of Euclidean Ramsey theory and of the arithmetic properties of analytic functions...
formulated the conjecture in 1948; It is one of many conjectures by Erdős
Erdos conjecture
The prolific mathematician Paul Erdős and his various collaborators made many famous mathematical conjectures, over a wide field of subjects.Some of these are the following:* The Cameron–Erdős conjecture on sum-free sets of integers, proved by Ben Green....
.
More formally, the conjecture states that, for every integer n ≥ 4, there exist positive integers x, y, and z such that
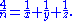
These unit fractions form an Egyptian fraction representation of the number 4/n. For instance, for n = 5, there are two solutions:
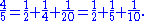
The restriction that x, y, and z be positive is essential to the difficulty of the problem, for if negative values were allowed the problem could be solved trivially. Also, if n is a composite number
Composite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
, n = pq, then an expansion for 4/n could be found immediately from an expansion for 4/p or 4/q. Therefore, if a counterexample to the Erdős–Straus conjecture exists, the smallest n forming a counterexample would have to be a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
, and it can be further restricted to one of six arithmetic progression
Arithmetic progression
In mathematics, an arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant...
s modulo 840. Computer searches have verified the truth of the conjecture up to n ≤ 1014, but proving it for all n remains an open problem.
Background
The search for expansions of rational numbers as sums of unit fractions dates to the mathematics of ancient EgyptEgyptian mathematics
Egyptian mathematics is the mathematics that was developed and used in Ancient Egypt from ca. 3000 BC to ca. 300 BC.-Overview:Written evidence of the use of mathematics dates back to at least 3000 BC with the ivory labels found at Tomb Uj at Abydos. These labels appear to have been used as tags for...
, in which Egyptian fraction expansions of this type were used as a notation for recording fractional quantities. The Egyptians produced tables such as the Rhind Mathematical Papyrus 2/n table
Rhind Mathematical Papyrus 2/n table
The Rhind Mathematical Papyrus contains, among other mathematical contents, a table of Egyptian fractions created from 2/n. The text reports 51 rational numbers converted to concise unit fraction series. The document was written in 1650 BCE by Ahmes...
of expansions of fractions of the form 2/n, most of which use either two or three terms.
The greedy algorithm for Egyptian fractions
Greedy algorithm for Egyptian fractions
In mathematics, the greedy algorithm for Egyptian fractions is a greedy algorithm, first described by Fibonacci, for transforming rational numbers into Egyptian fractions. An Egyptian fraction is a representation of an irreducible fraction as a sum of unit fractions, as e.g. 5/6 = 1/2 + 1/3...
, first described in 1202 by Fibonacci
Fibonacci
Leonardo Pisano Bigollo also known as Leonardo of Pisa, Leonardo Pisano, Leonardo Bonacci, Leonardo Fibonacci, or, most commonly, simply Fibonacci, was an Italian mathematician, considered by some "the most talented western mathematician of the Middle Ages."Fibonacci is best known to the modern...
in his book Liber Abaci
Liber Abaci
Liber Abaci is a historic book on arithmetic by Leonardo of Pisa, known later by his nickname Fibonacci...
, finds an expansion in which each successive term is the largest unit fraction that is no larger than the remaining number to be represented. For fractions of the form 2/n or 3/n, the greedy algorithm uses at most two or three terms respectively. More generally, it can be shown that a number of the form 3/n has a two-term expansion if and only if n has a factor congruent to 2 modulo 3, and requires three terms in any expansion otherwise.
Thus, for the numerators 2 and 3, the question of how many terms are needed in an Egyptian fraction is completely settled, and fractions of the form 4/n are the first case in which the worst-case length of an expansion remains unknown. The greedy algorithm produces expansions of length two, three, or four depending on the value of n modulo 4; when n is congruent to 1 modulo 4, the greedy algorithm produces four-term expansions. Therefore, the worst-case length of an Egyptian fraction of 4/n must be either three or four. The Erdős–Straus conjecture states that, in this case, as in the case for the numerator 3, the maximum number of terms in an expansion is three.
Modular identities
Multiplying both sides of the equation 4/n = 1/x + 1/y + 1/z by nxyz leads to an equivalent form 4xyz = n(xy + xz + yz) for the problem. As a polynomial equation with integer variables, this is an example of a Diophantine equationDiophantine equation
In mathematics, a Diophantine equation is an indeterminate polynomial equation that allows the variables to be integers only. Diophantine problems have fewer equations than unknown variables and involve finding integers that work correctly for all equations...
. The Hasse principle
Hasse principle
In mathematics, Helmut Hasse's local-global principle, also known as the Hasse principle, is the idea that one can find an integer solution to an equation by using the Chinese remainder theorem to piece together solutions modulo powers of each different prime number...
for Diophantine equations asserts that an integer solution of a Diophantine equation should be formed by combining solutions obtained modulo each possible prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
. On the face of it this principle makes little sense for the Erdős–Straus conjecture, as the equation 4xyz = n(xy + xz + yz) is easily solvable modulo any prime. Nevertheless, modular identities have proven a very important tool in the study of the conjecture.
For values of n satisfying certain congruence relations
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
, one can find an expansion for 4/n automatically as an instance of a polynomial identity. For instance, whenever n ≡ 2 (mod 3),4/n has the expansion
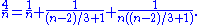
Here each of the three denominators n, (n − 2)/3 + 1, and n((n − 2)/3 + 1) is a polynomial of n, and each is an integer whenever n is 2 (mod 3).
The greedy algorithm for Egyptian fractions
Greedy algorithm for Egyptian fractions
In mathematics, the greedy algorithm for Egyptian fractions is a greedy algorithm, first described by Fibonacci, for transforming rational numbers into Egyptian fractions. An Egyptian fraction is a representation of an irreducible fraction as a sum of unit fractions, as e.g. 5/6 = 1/2 + 1/3...
finds a solution in three or fewer terms whenever n is not 1 or 17 (mod 24), and the n ≡ 17 (mod 24) case is covered by the 2 (mod 3) relation, so the only values of n for which these two methods do not find expansions in three or fewer terms are those congruent to 1 (mod 24).
If it were possible to find solutions such as the ones above for enough different moduli, forming a complete covering system of congruences, the problem would be solved. However, as showed, a polynomial identity that provides a solution for values of n congruent to r mod p can exist only when r is not a quadratic residue modulo p. For instance, 2 is a not a quadratic residue modulo 3, so the existence of an identity for values of n that are congruent to 2 modulo 3 does not contradict Mordell's result, but 1 is a quadratic residue modulo 3 so the result proves that there can be no similar identity for values of n that are congruent to 1 modulo 3.
Mordell lists polynomial identities that provide three-term Egyptian fractions for 4/n whenever n is 2 mod 3 (above), 3 mod 4, 5 mod 8, 2 or 3 mod 5, or 3, 5, or 6 mod 7. These identies cover all the numbers that are not quadratic residues for those bases. However, for larger bases, not all nonresidues are known to be covered by relations of this type. From Mordell's identities one can conclude that there exists a solution for all n except possibly those that are 1, 121, 169, 289, 361, or 529 modulo 840. 1009 is the smallest prime number that is not covered by this system of congruences. By combining larger classes of modular identities, Webb and others showed that the fraction of n in the interval [1,N] that can be counterexamples to the conjecture tends to zero in the limit as N goes to infinity.
Despite Mordell's result limiting the form these congruence identities can take, there is still some hope of using modular identities to prove the Erdős–Straus conjecture. No prime number can be a square, so by the Hasse-Minkowski theorem, whenever p is prime, there exists a larger prime q such that p is not a quadratic residue modulo q. One possible approach to proving the conjecture would be
to find for each prime p a larger prime q and a congruence solving the 4/n problem for n ≡ p (mod q); if this could be done, no prime p could be a counterexample to the conjecture and the conjecture would be true.
Computational verification
Various authors have performed brute-force searchBrute-force search
In computer science, brute-force search or exhaustive search, also known as generate and test, is a trivial but very general problem-solving technique that consists of systematically enumerating all possible candidates for the solution and checking whether each candidate satisfies the problem's...
es for counterexamples to the conjecture; these searches can be greatly sped up by considering only prime numbers that are not covered by known congruence relations. Searches of this type by Allan Swett confirmed that the conjecture is true for all n up to 1014.
The number of solutions
The number of distinct solutions to the 4/n problem, as a function of n, has also been found by computer searches for small n and appears to grow somewhat irregularly with n. Starting with n = 3, the numbers of distinct solutions with distinct denominators are- 1, 1, 2, 5, 5, 6, 4, 9, 7, 15, 4, 14, 33, 22, 4, 21, 9, ... .
Even for larger n there can be relatively few solutions; for instance there are only seven distinct solutions for n = 73.
have shown that the average number of solutions to the 4/n problem (averaged over the prime numbers up to n) grows polylogarithmic
Polylogarithmic
A polylogarithmic function in n is a polynomial in the logarithm of n,In computer science, polylogarithmic functions occur as the order of memory used by some algorithms .All polylogarithmic functions are...
ally in n. For some other Diophantine problems, it is possible to prove that a solution always exists by proving asymptotic lower bounds on the number of solutions, but proofs of this type exist primarily for problems in which the number of solutions grows polynomially, so Tao's result makes a solution of this type less likely. The proof of Tao's bound on the number of solutions involves the Bombieri–Vinogradov theorem
Bombieri–Vinogradov theorem
In mathematics, the Bombieri–Vinogradov theorem is a major result of analytic number theory, obtained in the mid-1960s. The first result of this kind was obtained by Barban in 1961 and the Bombieri–Vinogradov theorem is a refinement of Barban's result. The Bombieri-Vinogradov theorem is named...
, the Brun–Titchmarsh theorem
Brun–Titchmarsh theorem
In analytic number theory, the Brun–Titchmarsh theorem, named after Viggo Brun and Edward Charles Titchmarsh, is an upper bound on the distribution of prime numbers in arithmetic progression...
, and a system of modular identities, valid when n is congruent to −c or −1/c modulo 4ab, where a and b are any two coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
positive integers and c is any odd factor of a + b. For instance, setting a = b = 1 gives one of Mordell's identities, valid when n is 3 (mod 4).
Negative-number solutions
The restriction that x, y, and z be positive is essential to the difficulty of the problem, for if negative values were allowed the problem could be solved trivially via one of the two identities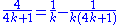
and
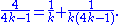
Alternatively, for any odd n, a three-term solution with one negative term is possible:
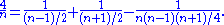
Generalizations
A generalized version of the conjecture states that, for any positive k there exists a number N such that, for all n ≥ N, there exists a solution in positive integers to k/n = 1/x + 1/y + 1/z. The version of this conjecture for k = 5 was made by Wacław Sierpiński, and the full conjecture is due to Andrzej SchinzelAndrzej Schinzel
Andrzej Bobola Maria Schinzel is a Polish mathematician, studying mainly number theory.- Biography :Schinzel received his Ph.D...
.
Even if the generalized conjecture is false for any fixed value of k, then the number of fractions k/n with n in the range from 1 to N that do not have three-term expansions must grow only sublinearly as a function of N. In particular, if the Erdős–Straus conjecture itself (the case k = 4) is false, then the number of counterexamples grows only sublinearly. Even more strongly, for any fixed k, only a sublinear number of values of n need more than two terms in their Egyptian fraction expansions. The generalized version of the conjecture is equivalent to the statement that the number of unexpandable fractions is not just sublinear but bounded.
When n is an odd number, by analogy to the problem of odd greedy expansions for Egyptian fractions, one may ask for solutions to k/n = 1/x + 1/y + 1/z in which x, y, and z are distinct positive odd numbers. Solutions to this equation are known to always exist for the case that k = 3.
External links
- Counting the number of solutions to the Erdös-Straus equation on unit fractions, Terence TaoTerence TaoTerence Chi-Shen Tao FRS is an Australian mathematician working primarily on harmonic analysis, partial differential equations, combinatorics, analytic number theory and representation theory...
, July 31, 2011.

