
Brun–Titchmarsh theorem
Encyclopedia
In analytic number theory
, the Brun–Titchmarsh theorem, named after Viggo Brun
and Edward Charles Titchmarsh
, is an upper bound
on the distribution of prime numbers in arithmetic progression
. It states that, if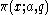 counts the number of primes p congruent to a modulo q with p ≤ x, then
counts the number of primes p congruent to a modulo q with p ≤ x, then

for all q < x. The result is proved by sieve methods.
By contrast, Dirichlet's theorem on arithmetic progressions
gives an asymptotic result, which may be expressed in the form
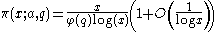
but this can only be proved to hold for the more restricted range q < (log x)c for constant c: this is the Siegel–Walfisz theorem.
Analytic number theory
In mathematics, analytic number theory is a branch of number theory that uses methods from mathematical analysis to solve problems about the integers. It is often said to have begun with Dirichlet's introduction of Dirichlet L-functions to give the first proof of Dirichlet's theorem on arithmetic...
, the Brun–Titchmarsh theorem, named after Viggo Brun
Viggo Brun
Viggo Brun was a Norwegian mathematician.He studied at the University of Oslo and began research at the University of Göttingen in 1910. In 1923, Brun became a professor at the Technical University in Trondheim and in 1946 a professor at the University of Oslo...
and Edward Charles Titchmarsh
Edward Charles Titchmarsh
Edward Charles "Ted" Titchmarsh was a leading British mathematician.He was educated at King Edward VII School and Balliol College, Oxford, where he began his studies in October 1917....
, is an upper bound
Upper bound
In mathematics, especially in order theory, an upper bound of a subset S of some partially ordered set is an element of P which is greater than or equal to every element of S. The term lower bound is defined dually as an element of P which is lesser than or equal to every element of S...
on the distribution of prime numbers in arithmetic progression
Primes in arithmetic progression
In number theory, the phrase primes in arithmetic progression refers to at least three prime numbers that are consecutive terms in an arithmetic progression, for example the primes ....
. It states that, if
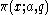 counts the number of primes p congruent to a modulo q with p ≤ x, then
counts the number of primes p congruent to a modulo q with p ≤ x, then
for all q < x. The result is proved by sieve methods.
By contrast, Dirichlet's theorem on arithmetic progressions
Dirichlet's theorem on arithmetic progressions
In number theory, Dirichlet's theorem, also called the Dirichlet prime number theorem, states that for any two positive coprime integers a and d, there are infinitely many primes of the form a + nd, where n ≥ 0. In other words, there are infinitely many primes which are...
gives an asymptotic result, which may be expressed in the form
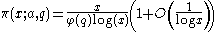
but this can only be proved to hold for the more restricted range q < (log x)c for constant c: this is the Siegel–Walfisz theorem.

