
Enneahedron
Encyclopedia
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
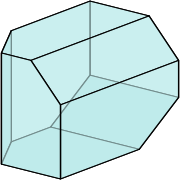
, a enneahedron (or nonahedron) is a polyhedron
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
with 9 faces
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
. There are 2606 topologically
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
distinct enneahedra and none are regular
Regular polyhedron
A regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags...
, so this name is ambiguous.
Examples
The most familiar enneahedra are the octagonalOctagonal
Octagonal is a retired champion New Zealand-bred, Australian raced Thoroughbred racehorse, also known as 'The Big O' or 'Occy'. He was by the champion sire Zabeel, out of the champion broodmare Eight Carat, who also produced Group One winners Mouawad, Kaapstad, Diamond Lover and Marquise.Trained...
pyramid
Pyramid (geometry)
In geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle. It is a conic solid with polygonal base....
and the heptagonal prism
Heptagonal prism
In geometry, the heptagonal prism is the fifth of the infinite set of convex prisms formed by square sides and two regular polygon caps, in this case two heptagons....
. The heptagonal prism is a uniform polyhedron
Prismatic uniform polyhedron
In geometry, a prismatic uniform polyhedron is a uniform polyhedron with dihedral symmetry. They exist in two infinite families, the uniform prisms and the uniform antiprisms...
, with two regular heptagon faces and seven square faces. The octagonal pyramid has eight isosceles triangular faces around a regualar octagonal base. Two more enneahedra are also found among the Johnson solid
Johnson solid
In geometry, a Johnson solid is a strictly convex polyhedron, each face of which is a regular polygon, but which is not uniform, i.e., not a Platonic solid, Archimedean solid, prism or antiprism. There is no requirement that each face must be the same polygon, or that the same polygons join around...
s: the elongated square pyramid
Elongated square pyramid
In geometry, the elongated square pyramid is one of the Johnson solids . As the name suggests, it can be constructed by elongating a square pyramid by attaching a cube to its square base...
and the elongated triangular bipyramid.
The three-dimensional associahedron
Associahedron
In mathematics, an associahedron or Stasheff polytope Kn is a convex polytope in which each vertex corresponds to a way of correctly inserting opening and closing parentheses in a word of n letters and the edges correspond to single application of the associativity rule.Initially Jim Stasheff...
, a near-miss Johnson solid
Near-miss Johnson solid
In geometry, a near-miss Johnson solid is a strictly convex polyhedron, where every face is a regular or nearly regular polygon, and excluding the 5 Platonic solids, the 13 Archimedean solids, the infinite set of prisms, the infinite set of antiprisms, and the 92 Johnson solids.The set of...
with six pentagonal faces and three quadrilateral faces, is an enneahedron. Five Johnson solids have enneahedral duals: the triangular cupola
Triangular cupola
In geometry, the triangular cupola is one of the Johnson solids . It can be seen as half a cuboctahedron.The 92 Johnson solids were named and described by Norman Johnson in 1966.-Formulae:...
, gyroelongated square pyramid
Gyroelongated square pyramid
In geometry, the gyroelongated square pyramid is one of the Johnson solids . As its name suggests, it can be constructed by taking a square pyramid and "gyroelongating" it, which in this case involves joining a square antiprism to its base....
, self-dual elongated square pyramid
Elongated square pyramid
In geometry, the elongated square pyramid is one of the Johnson solids . As the name suggests, it can be constructed by elongating a square pyramid by attaching a cube to its square base...
, triaugmented triangular prism
Triaugmented triangular prism
In geometry, the triaugmented triangular prism is one of the Johnson solids . As the name suggests, it can be constructed by attaching square pyramids to each of the three equatorial faces of the triangular prism...
(whose dual is the associahedron), and tridiminished icosahedron
Tridiminished icosahedron
In geometry, the tridiminished icosahedron is one of the Johnson solids .The 92 Johnson solids were named and described by Norman Johnson in 1966.- Related polytopes :...
.
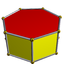 Heptagonal prism Heptagonal prism In geometry, the heptagonal prism is the fifth of the infinite set of convex prisms formed by square sides and two regular polygon caps, in this case two heptagons.... |
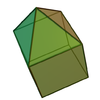 Elongated square pyramid Elongated square pyramid In geometry, the elongated square pyramid is one of the Johnson solids . As the name suggests, it can be constructed by elongating a square pyramid by attaching a cube to its square base... |
 Elongated triangular bipyramid |
Dual of triangular cupola Triangular cupola In geometry, the triangular cupola is one of the Johnson solids . It can be seen as half a cuboctahedron.The 92 Johnson solids were named and described by Norman Johnson in 1966.-Formulae:... |
Dual of gyroelongated square pyramid Gyroelongated square pyramid In geometry, the gyroelongated square pyramid is one of the Johnson solids . As its name suggests, it can be constructed by taking a square pyramid and "gyroelongating" it, which in this case involves joining a square antiprism to its base.... |
Dual of tridiminished icosahedron Tridiminished icosahedron In geometry, the tridiminished icosahedron is one of the Johnson solids .The 92 Johnson solids were named and described by Norman Johnson in 1966.- Related polytopes :... |
The Herschel graph
Herschel graph
In graph theory, a branch of mathematics, the Herschel graph is a bipartite undirected graph with 11 vertices and 18 edges, the smallest non-Hamiltonian polyhedral graph...
also represents the vertices and edges of an enneahedron, with all of its faces quadrilaterals. It is the simplest polyhedron without a Hamiltonian cycle, the only enneahedron in which all faces have the same number of edges, and one of only three bipartite
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
enneahedra.
The two smallest isospectral
Spectral graph theory
In mathematics, spectral graph theory is the study of properties of a graph in relationship to the characteristic polynomial, eigenvalues, and eigenvectors of matrices associated to the graph, such as its adjacency matrix or Laplacian matrix....
polyhedral graph
Polyhedral graph
In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs...
s are enneahedra with eight vertices each.
Space-filling enneahedra

Rhombic dodecahedron
In geometry, the rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.-Properties:...
in half through the long diagonals of four of its faces results in a self-dual enneahedron with one large square face, four rhombus faces, and four isosceles triangle faces that can be used to tessellate
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
three-dimensional space. The same shape, in an elongated form that still tiles space, can be seen atop the rear side towers of the 12th-century Romanesque Basilica of Our Lady (Maastricht)
Basilica of Our Lady (Maastricht)
The Roman catholic Basilica of Our Lady is a Romanesque basilica in Maastricht, The Netherlands, dedicated to Our Lady of the Assumption. The church is often referred to as the Star of the Sea, after the church's main devotion, Our Lady, Star of the Sea...
. The towers themselves, with their four sides, four roof facets, and square base, form another space-filling enneahedron.
More generally, found at least 40 topologically distinct space-filling enneahedra.
Topologically distinct enneahedra
There are 2606 topologically distinct convex enneahedra, excluding mirror images. These can be divided into subsets of 8, 74, 296, 633, 768, 558, 219, 50, with 7 to 14 vertices respectively. A table of these numbers, together with a detailed description of the nine-vertex enneahedra, was first published in the 1870s by Thomas Kirkman.External links
- Enumeration of Polyhedra by Steven Dutch

