Empirical process
Encyclopedia
The study of empirical processes is a branch of mathematical statistics
and a sub-area of probability theory
. It is a generalization of the central limit theorem
for empirical measure
s. Applications of the theory of empirical processes arise in non-parametric statistics
.
s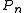
uniformly converge to the probability measure
P (see Glivenko–Cantelli theorem). The theory of Empirical processes provides the rate of this convergence.
A centered and scaled version of the empirical measure is the signed measure
It induces a map on measurable functions f given by
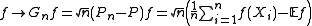
By the central limit theorem
,
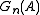converges in distribution to a normal random variable N(0, P(A)(1 − P(A))) for fixed measurable set A. Similarly, for a fixed function f, 
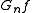converges in distribution to a normal random variable 
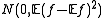, provided that 
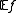and 
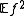exist.
Definition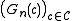
is called an empirical process indexed by 
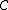, a collection of measurable subsets of S.
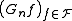is called an empirical process indexed by 
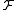, a collection of measurable functions from S to 
.
A significant result in the area of empirical processes is Donsker's theorem
. It has led to a study of the Donsker classes such that empirical processes indexed by these classes converge weakly to a certain Gaussian process
. It can be shown that the Donsker classes are Glivenko–Cantelli classes, the converse is not true in general.
s. For real-valued iid random variables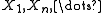
they are given by
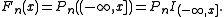
In this case, empirical processes are indexed by a class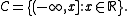
It has been shown that 
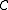is a Donsker class, in particular,
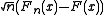converges weakly in 
to a Brownian bridge
B(F(x)) .
Mathematical statistics
Mathematical statistics is the study of statistics from a mathematical standpoint, using probability theory as well as other branches of mathematics such as linear algebra and analysis...
and a sub-area of probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
. It is a generalization of the central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
for empirical measure
Empirical measure
In probability theory, an empirical measure is a random measure arising from a particular realization of a sequence of random variables. The precise definition is found below. Empirical measures are relevant to mathematical statistics....
s. Applications of the theory of empirical processes arise in non-parametric statistics
Non-parametric statistics
In statistics, the term non-parametric statistics has at least two different meanings:The first meaning of non-parametric covers techniques that do not rely on data belonging to any particular distribution. These include, among others:...
.
Definition
It is known that under certain conditions empirical measureEmpirical measure
In probability theory, an empirical measure is a random measure arising from a particular realization of a sequence of random variables. The precise definition is found below. Empirical measures are relevant to mathematical statistics....
s
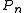uniformly converge to the probability measureProbability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
P (see Glivenko–Cantelli theorem). The theory of Empirical processes provides the rate of this convergence.
A centered and scaled version of the empirical measure is the signed measure
Signed measure
In mathematics, signed measure is a generalization of the concept of measure by allowing it to have negative values. Some authors may call it a charge, by analogy with electric charge, which is a familiar distribution that takes on positive and negative values.-Definition:There are two slightly...
It induces a map on measurable functions f given by
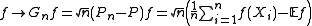
By the central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
,
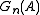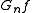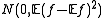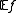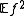converges in distribution to a normal random variable N(0, P(A)(1 − P(A))) for fixed measurable set A. Similarly, for a fixed function f, converges in distribution to a normal random variable , provided that and exist.Definition
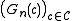is called an empirical process indexed by 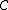, a collection of measurable subsets of S. 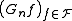is called an empirical process indexed by 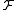, a collection of measurable functions from S to .A significant result in the area of empirical processes is Donsker's theorem
Donsker's theorem
In probability theory, Donsker's theorem, named after M. D. Donsker, identifies a certain stochastic process as a limit of empirical processes. It is sometimes called the functional central limit theorem....
. It has led to a study of the Donsker classes such that empirical processes indexed by these classes converge weakly to a certain Gaussian process
Gaussian process
In probability theory and statistics, a Gaussian process is a stochastic process whose realisations consist of random values associated with every point in a range of times such that each such random variable has a normal distribution...
. It can be shown that the Donsker classes are Glivenko–Cantelli classes, the converse is not true in general.
Example
As an example, consider empirical distribution functionEmpirical distribution function
In statistics, the empirical distribution function, or empirical cdf, is the cumulative distribution function associated with the empirical measure of the sample. This cdf is a step function that jumps up by 1/n at each of the n data points. The empirical distribution function estimates the true...
s. For real-valued iid random variables
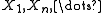they are given by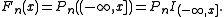In this case, empirical processes are indexed by a class
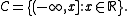It has been shown that 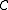is a Donsker class, in particular, 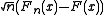converges weakly in to a Brownian bridgeBrownian bridge
A Brownian bridge is a continuous-time stochastic process B whose probability distribution is the conditional probability distribution of a Wiener process W given the condition that B = B = 0.The expected value of the bridge is zero, with variance t, implying that the most...
B(F(x)) .
See also
- Khmaladze transformationKhmaladze transformationThe Khmaladze Transformation is a statistical tool.Consider the sequence of empirical distribution functions F_n based on asequence of i.i.d random variables, X_1,\ldots, X_n, as n increases.Suppose F is the hypothetical distribution function of...
- Weak convergence of measures
- Glivenko-Cantelli theoremGlivenko-Cantelli theoremIn the theory of probability, the Glivenko–Cantelli theorem, named after Valery Ivanovich Glivenko and Francesco Paolo Cantelli, determines the asymptotic behaviour of the empirical distribution function as the number of independent and identically distributed observations grows...
External links
- Empirical Processes: Theory and Applications, by David Pollard, a textbook available online.
- Introduction to Empirical Processes and Semiparametric Inference, by Michael Kosorok, another textbook available online.