
Ehrenfest theorem
Encyclopedia
The Ehrenfest theorem, named after Paul Ehrenfest
, the Austrian physicist and mathematician, relates the time derivative
of the expectation value
for a quantum mechanical
operator
to the commutator
of that operator with the Hamiltonian
of the system. It is
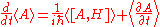
where A is some QM operator and is its expectation value. Ehrenfest's theorem is obvious in the Heisenberg picture
is its expectation value. Ehrenfest's theorem is obvious in the Heisenberg picture
of quantum mechanics, where it is just the expectation value of the Heisenberg equation of motion.
Ehrenfest's theorem is closely related to Liouville's theorem
from Hamiltonian mechanics
, which involves the Poisson bracket
instead of a commutator. In fact, it is a rule of thumb
that a theorem in quantum mechanics which contains a commutator can be turned into a theorem in classical mechanics by changing the commutator into a Poisson bracket and multiplying by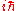 . This causes the operator expectation values to obey their corresponding classical equations of motion provided the Hamiltonian is at most quadratic in the coordinates and momenta. Otherwise, the equations still may hold approximately, provided fluctuations are small.
. This causes the operator expectation values to obey their corresponding classical equations of motion provided the Hamiltonian is at most quadratic in the coordinates and momenta. Otherwise, the equations still may hold approximately, provided fluctuations are small.
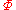 . If we want to know the instantaneous time derivative of the expectation value of A, that is, by definition
. If we want to know the instantaneous time derivative of the expectation value of A, that is, by definition
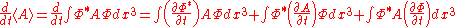

where we are integrating over all space. If we apply the Schrödinger equation
, we find that
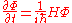
and

Notice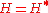 because the Hamiltonian
because the Hamiltonian
is hermitian. Placing this into the above equation we have
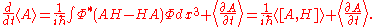
Often (but not always) the operator A is time independent, so that its derivative is zero and we can ignore the last term.
moving in a potential
, the Hamiltonian is simply
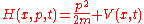
where is just the location of the particle. Suppose we wanted to know the instantaneous change in momentum
is just the location of the particle. Suppose we wanted to know the instantaneous change in momentum 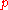 . Using Ehrenfest's theorem, we have
. Using Ehrenfest's theorem, we have
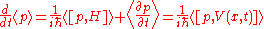
since the operator commutes with itself and has no time dependence. By expanding the right-hand-side, replacing p by
commutes with itself and has no time dependence. By expanding the right-hand-side, replacing p by 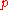 , we get
, we get
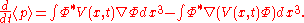
After applying the product rule
on the second term, we have

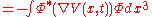

but we recognize this as Newton's second law. This is an example of the correspondence principle
, the result manifests as Newton's second law in the case of having so many particles that the net motion is given exactly by the expectation value of a single particle.
Similarly we can obtain the instantaneous change in the position expectation value.
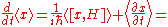
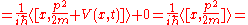
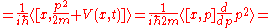

This result is again in accord with the classical equation.
Paul Ehrenfest
Paul Ehrenfest was an Austrian and Dutch physicist, who made major contributions to the field of statistical mechanics and its relations with quantum mechanics, including the theory of phase transition and the Ehrenfest theorem.- Biography :Paul Ehrenfest was born and grew up in Vienna in a Jewish...
, the Austrian physicist and mathematician, relates the time derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of the expectation value
Expectation value (quantum mechanics)
In quantum mechanics, the expectation value is the predicted mean value of the result of an experiment. Despite the name, it is not the most probable value of a measurement...
for a quantum mechanical
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
operator
Operator (physics)
In physics, an operator is a function acting on the space of physical states. As a resultof its application on a physical state, another physical state is obtained, very often along withsome extra relevant information....
to the commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
of that operator with the Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
of the system. It is
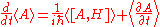
where A is some QM operator and
 is its expectation value. Ehrenfest's theorem is obvious in the Heisenberg picture
is its expectation value. Ehrenfest's theorem is obvious in the Heisenberg pictureHeisenberg picture
In physics, the Heisenberg picture is a formulation of quantum mechanics in which the operators incorporate a dependency on time, but the state vectors are time-independent. It stands in contrast to the Schrödinger picture in which the operators are constant and the states evolve in time...
of quantum mechanics, where it is just the expectation value of the Heisenberg equation of motion.
Ehrenfest's theorem is closely related to Liouville's theorem
Liouville's theorem (Hamiltonian)
In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical and Hamiltonian mechanics...
from Hamiltonian mechanics
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
, which involves the Poisson bracket
Poisson bracket
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
instead of a commutator. In fact, it is a rule of thumb
Rule of thumb
A rule of thumb is a principle with broad application that is not intended to be strictly accurate or reliable for every situation. It is an easily learned and easily applied procedure for approximately calculating or recalling some value, or for making some determination...
that a theorem in quantum mechanics which contains a commutator can be turned into a theorem in classical mechanics by changing the commutator into a Poisson bracket and multiplying by
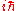 . This causes the operator expectation values to obey their corresponding classical equations of motion provided the Hamiltonian is at most quadratic in the coordinates and momenta. Otherwise, the equations still may hold approximately, provided fluctuations are small.
. This causes the operator expectation values to obey their corresponding classical equations of motion provided the Hamiltonian is at most quadratic in the coordinates and momenta. Otherwise, the equations still may hold approximately, provided fluctuations are small.Derivation
Suppose some system is presently in a quantum state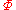 . If we want to know the instantaneous time derivative of the expectation value of A, that is, by definition
. If we want to know the instantaneous time derivative of the expectation value of A, that is, by definition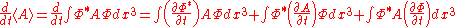

where we are integrating over all space. If we apply the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
, we find that
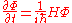
and

Notice
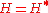 because the Hamiltonian
because the HamiltonianHamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
is hermitian. Placing this into the above equation we have
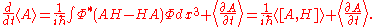
Often (but not always) the operator A is time independent, so that its derivative is zero and we can ignore the last term.
General example
For the very general example of a massive particleElementary particle
In particle physics, an elementary particle or fundamental particle is a particle not known to have substructure; that is, it is not known to be made up of smaller particles. If an elementary particle truly has no substructure, then it is one of the basic building blocks of the universe from which...
moving in a potential
Potential
*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...
, the Hamiltonian is simply
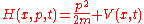
where
 is just the location of the particle. Suppose we wanted to know the instantaneous change in momentum
is just the location of the particle. Suppose we wanted to know the instantaneous change in momentum 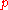 . Using Ehrenfest's theorem, we have
. Using Ehrenfest's theorem, we have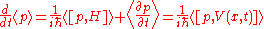
since the operator
 commutes with itself and has no time dependence. By expanding the right-hand-side, replacing p by
commutes with itself and has no time dependence. By expanding the right-hand-side, replacing p by 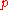 , we get
, we get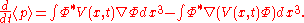
After applying the product rule
Product rule
In calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
on the second term, we have

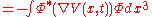

but we recognize this as Newton's second law. This is an example of the correspondence principle
Correspondence principle
In physics, the correspondence principle states that the behavior of systems described by the theory of quantum mechanics reproduces classical physics in the limit of large quantum numbers....
, the result manifests as Newton's second law in the case of having so many particles that the net motion is given exactly by the expectation value of a single particle.
Similarly we can obtain the instantaneous change in the position expectation value.
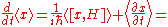
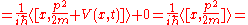
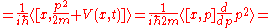

This result is again in accord with the classical equation.

