Discrete Fourier transform (general)
Encyclopedia
This article is about the discrete Fourier transform (DFT) over any field
(including finite field
s), commonly called a number-theoretic transform (NTT) in the case of finite fields. For specific information on the discrete Fourier transform over the complex number
s, see discrete Fourier transform
.
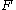be any field
, let
be an integer, and let 
be a primitive 
th root of unity.
We assume
lies in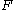 
.
The discrete Fourier transform maps an n-tuple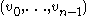
of elements of 
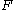to another n-tuple 
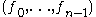of elements of 
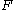according to the following formula:
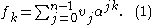
By convention, the tuple
is said to be in the time domain and the index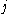 
is called time. The tuple 
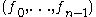is said to be in the frequency domain and the index 
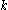is called frequency. The tuple 
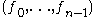is also called the spectrum
of
. This terminology derives from the applications of Fourier transforms in signal processing
.
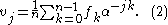
Proof: first, note that whenever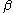
is an
th root of unity, then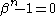 
.
If moreover
, then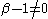 
, and therefore
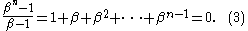
Substituting (1) into the right-hand-side of (2), we get
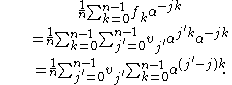
This is exactly equal to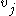
, because
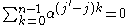when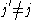 
(by (3) with 
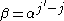), and
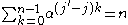when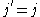 
.
. In matrix notation, the discrete Fourier transform is expressed as follows: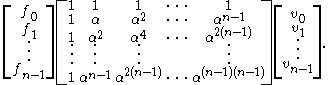
The matrix for this transformation is called the DFT matrix
.
Similarly, the matrix notation for the inverse Fourier transform is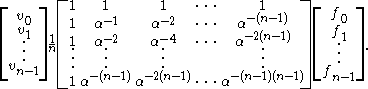
-tuple 
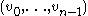with a formal polynomial
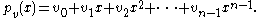
By writing out the summation in the definition of the discrete Fourier transform (1), we obtain:
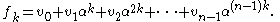
This means that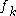
is just the value of the polynomial 
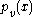for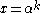 
, i.e.,
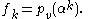
The Fourier transform can therefore be seen to relate the coefficients and the values of a polynomial: the coefficients are in the time-domain, and the values are in the frequency domain. Here, of course, it is important that the polynomial is evaluated at the
th roots of unity, which are exactly the powers of 
.
Similarly, the definition of the inverse Fourier transform (2) can be written:
With
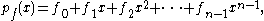
this means that
We can summarize this as follows: if the values of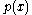
are the coefficients of 
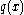, then the values of 
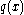are the coefficients of 
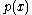, up to a scalar factor and reordering.
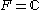is the field of complex numbers, then the 
th roots of unity can be visualized as points on the unit circle
of the complex plane
. In this case, one usually takes
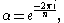
which yields the usual formula for the complex discrete Fourier transform
:
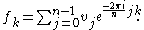
Over the complex numbers, it is often customary to normalize the formulas for the DFT and inverse DFT by using the scalar factor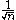
in both formulas, rather than 
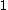in the formula for the DFT and 
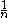in the formula for the inverse DFT. With this normalization, the DFT matrix is then unitary.
Note that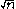
does not make sense in an arbitrary field.
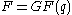is a finite field
, where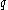
is a prime
power, then the existence of a primitive
th root automatically implies that 
divides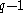 
(because the multiplicative order
of each element must divide the size of the multiplicative group
of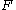
, which is 
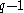). This in particular ensures that 
is invertible, so that the notation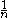 
in (2) makes sense.
An application of the discrete Fourier transform over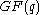
is the reduction of Reed-Solomon codes to BCH code
s in coding theory
.
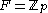, the integers modulo a prime 
. In this case, primitive
th roots of unity exists whenever 
divides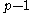 
, so we have 
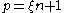for a positive integer 
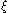. Specifically, let 
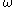be a primitive 
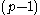st root of unity, then an 
th root of unity 
can be found by letting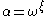 
.
The number-theoretic transform can further be generalized to operate on elements of the ring
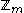, even when the modulus 
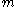is not prime. Various special cases of the number theoretic transform such as the Fermat Number Transform or Mersenne Number Transform use a composite modulus (see e.g. Schönhage–Strassen algorithm).
For the number theoretic transform to work in a useful way when the modulus is composite (for the inverse algorithm, convolution etc. to work), it suffices that the modulus is chosen so that a primitive root of order
exists (where 
is the transform length), and such that the multiplicative inverse of 
exists. Note that if 
is a primitive root of order 
, then 
is automatically invertible with inverse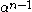 
.
, including the inverse transform, the convolution theorem
, and most fast Fourier transform
(FFT) algorithms, depend only on the property that the kernel of the transform is a primitive root of unity. These properties also hold, with identical proofs, over arbitrary fields. This analogy can be formalized by the field with one element
, considering any field with a primitive nth root of unity as an algebra over the extension field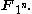
In particular, the applicability of
fast Fourier transform
algorithms to compute the NTT, combined with the convolution theorem, mean that the number-theoretic transform gives an efficient way to compute exact convolution
s of integer sequences. While the complex DFT can perform the same task, it is susceptible to round-off error
in finite-precision floating point
arithmetic; the NTT has no round-off because it deals purely with fixed-size integers that can be exactly represented.
computes the DFT
), it is often desirable that the transform length is also highly composite, e.g. a power of two
. However, there are specialized fast Fourier transform algorithms for finite fields, such as Wang and Zhu's algorithm, which are efficient regardless of whether the transform length factors.
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
(including finite field
Finite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s), commonly called a number-theoretic transform (NTT) in the case of finite fields. For specific information on the discrete Fourier transform over the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, see discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
.
Definition
Let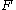 be any fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
, let
be an integer, and let be a primitive th root of unity.We assume
lies in 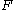.The discrete Fourier transform maps an n-tuple
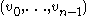of elements of 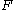to another n-tuple 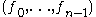of elements of 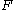according to the following formula: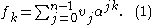By convention, the tuple
is said to be in the time domain and the index 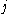is called time. The tuple 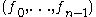is said to be in the frequency domain and the index 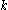is called frequency. The tuple 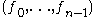is also called the spectrumFrequency spectrum
The frequency spectrum of a time-domain signal is a representation of that signal in the frequency domain. The frequency spectrum can be generated via a Fourier transform of the signal, and the resulting values are usually presented as amplitude and phase, both plotted versus frequency.Any signal...
of
. This terminology derives from the applications of Fourier transforms in signal processingSignal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
.
Inverse
The inverse of the discrete Fourier transform is given as: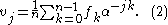Proof: first, note that whenever
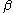is anth root of unity, then 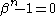.If moreover
, then 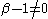, and therefore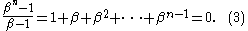Substituting (1) into the right-hand-side of (2), we get
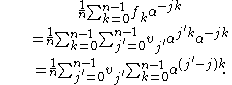
This is exactly equal to
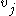, because 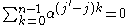when 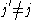(by (3) with 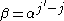), and 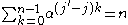when 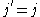.Matrix formulation
Since the discrete Fourier transform is a linear operator, it can be described by matrix multiplicationMatrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
. In matrix notation, the discrete Fourier transform is expressed as follows:
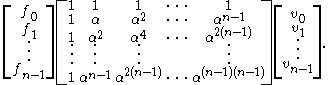
The matrix for this transformation is called the DFT matrix
DFT matrix
A DFT matrix is an expression of a discrete Fourier transform as a matrix multiplication.-Definition:An N-point DFT is expressed as an N-by-N matrix multiplication as X = W x, where x is the original input signal, and X is the DFT of the signal.The transformation W of size N\times N can be defined...
.
Similarly, the matrix notation for the inverse Fourier transform is
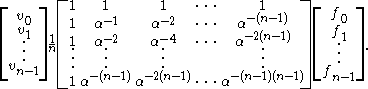
Polynomial formulation
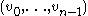Sometimes it is convenient to identify an-tuple with a formal polynomial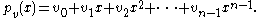By writing out the summation in the definition of the discrete Fourier transform (1), we obtain:
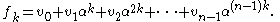
This means that
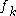is just the value of the polynomial 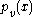for 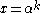, i.e.,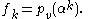The Fourier transform can therefore be seen to relate the coefficients and the values of a polynomial: the coefficients are in the time-domain, and the values are in the frequency domain. Here, of course, it is important that the polynomial is evaluated at the
th roots of unity, which are exactly the powers of .Similarly, the definition of the inverse Fourier transform (2) can be written:
With
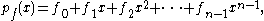
this means that
We can summarize this as follows: if the values of
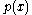are the coefficients of 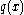, then the values of 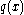are the coefficients of 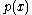, up to a scalar factor and reordering.Complex numbers
If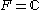 is the field of complex numbers, then the th roots of unity can be visualized as points on the unit circleUnit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
of the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
. In this case, one usually takes
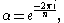
which yields the usual formula for the complex discrete Fourier transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
:
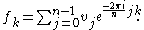
Over the complex numbers, it is often customary to normalize the formulas for the DFT and inverse DFT by using the scalar factor
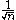in both formulas, rather than 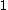in the formula for the DFT and 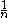in the formula for the inverse DFT. With this normalization, the DFT matrix is then unitary.Note that
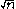does not make sense in an arbitrary field.Finite fields
If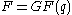 is a finite fieldFinite field
In abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
, where
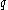is a primePrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
power, then the existence of a primitive
th root automatically implies that divides 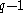(because the multiplicative orderMultiplicative order
In number theory, given an integer a and a positive integer n with gcd = 1, the multiplicative order of a modulo n is the smallest positive integer k withThe order of a modulo n is usually written ordn, or On.- Example :To determine the multiplicative order of 4 modulo 7, we compute 42 = 16 ≡ 2 ...
of each element must divide the size of the multiplicative group
Multiplicative group
In mathematics and group theory the term multiplicative group refers to one of the following concepts, depending on the context*any group \scriptstyle\mathfrak \,\! whose binary operation is written in multiplicative notation ,*the underlying group under multiplication of the invertible elements of...
of
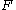, which is 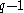). This in particular ensures that is invertible, so that the notation 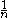in (2) makes sense.An application of the discrete Fourier transform over
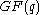is the reduction of Reed-Solomon codes to BCH codeBCH code
In coding theory the BCH codes form a class of parameterised error-correcting codes which have been the subject of much academic attention in the last fifty years. BCH codes were invented in 1959 by Hocquenghem, and independently in 1960 by Bose and Ray-Chaudhuri...
s in coding theory
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
.
Number-theoretic transform
The so-called number-theoretic transform (NTT) is obtained by specializing the discrete Fourier transform to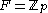, the integers modulo a prime Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
. In this case, primitive
th roots of unity exists whenever divides 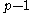, so we have 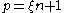for a positive integer 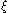. Specifically, let 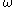be a primitive 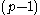st root of unity, then an th root of unity can be found by letting 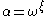.The number-theoretic transform can further be generalized to operate on elements of the ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
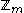, even when the modulus 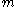is not prime. Various special cases of the number theoretic transform such as the Fermat Number Transform or Mersenne Number Transform use a composite modulus (see e.g. Schönhage–Strassen algorithm).For the number theoretic transform to work in a useful way when the modulus is composite (for the inverse algorithm, convolution etc. to work), it suffices that the modulus is chosen so that a primitive root of order
exists (where is the transform length), and such that the multiplicative inverse of exists. Note that if is a primitive root of order , then is automatically invertible with inverse 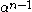.Properties
Most of the important attributes of the complex DFTDiscrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
, including the inverse transform, the convolution theorem
Convolution theorem
In mathematics, the convolution theorem states that under suitableconditions the Fourier transform of a convolution is the pointwise product of Fourier transforms. In other words, convolution in one domain equals point-wise multiplication in the other domain...
, and most fast Fourier transform
Fast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
(FFT) algorithms, depend only on the property that the kernel of the transform is a primitive root of unity. These properties also hold, with identical proofs, over arbitrary fields. This analogy can be formalized by the field with one element
Field with one element
In mathematics, the field with one element is a suggestive name for an object that should behave similarly to a finite field with a single element, if such a field could exist. This object is denoted F1, or, in a French-English pun, Fun...
, considering any field with a primitive nth root of unity as an algebra over the extension field
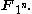
In particular, the applicability of
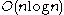fast Fourier transformFast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
algorithms to compute the NTT, combined with the convolution theorem, mean that the number-theoretic transform gives an efficient way to compute exact convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
s of integer sequences. While the complex DFT can perform the same task, it is susceptible to round-off error
Round-off error
A round-off error, also called rounding error, is the difference between the calculated approximation of a number and its exact mathematical value. Numerical analysis specifically tries to estimate this error when using approximation equations and/or algorithms, especially when using finitely many...
in finite-precision floating point
Floating point
In computing, floating point describes a method of representing real numbers in a way that can support a wide range of values. Numbers are, in general, represented approximately to a fixed number of significant digits and scaled using an exponent. The base for the scaling is normally 2, 10 or 16...
arithmetic; the NTT has no round-off because it deals purely with fixed-size integers that can be exactly represented.
Fast algorithms
For the implementation of a "fast" algorithm (similar to how FFTFast Fourier transform
A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...
computes the DFT
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
), it is often desirable that the transform length is also highly composite, e.g. a power of two
Power of two
In mathematics, a power of two means a number of the form 2n where n is an integer, i.e. the result of exponentiation with as base the number two and as exponent the integer n....
. However, there are specialized fast Fourier transform algorithms for finite fields, such as Wang and Zhu's algorithm, which are efficient regardless of whether the transform length factors.
See also
- Discrete Fourier transform (complex)Discrete Fourier transformIn mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
- Gauss sumGauss sumIn mathematics, a Gauss sum or Gaussian sum is a particular kind of finite sum of roots of unity, typicallyG := G= \sum \chi\cdot \psi...
- ConvolutionConvolutionIn mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
- Multiplication algorithmMultiplication algorithmA multiplication algorithm is an algorithm to multiply two numbers. Depending on the size of the numbers, different algorithms are in use...
External links
- http://www.apfloat.org/ntt.html