Diagrammatic reasoning
Encyclopedia
Diagrammatic reasoning is reasoning by means of visual representation
s. The study of diagrammatic reasoning is about the understanding of concepts and ideas, visualized with the use of diagram
s and image
ry instead of by linguistic
or algebra
ic means.
, commonly interpreted as universal characteristic, or universal character in English, is a universal and formal language imagined by the German philosopher Gottfried Leibniz
able to express mathematical, scientific, and metaphysical concepts. Leibniz thus hoped to create a language usable within the framework of a universal logical calculation or calculus ratiocinator
.
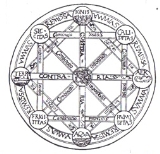
Since the characteristica universalis is diagrammatic and employs pictograms (below left), the diagrams in Leibniz's work warrant close study. On at least two occasions, Leibniz illustrated his philosophical reasoning with diagrams. One diagram, the frontispiece to his 1666 De Arte Combinatoria
(On the Art of Combinations), represents the Aristotelian theory of how all material things are formed from combinations of the elements earth, water, air, and fire.
 These four elements make up the four corners of a diamond (see picture to right). Opposing pairs of these are joined by a bar labeled "contraries" (earth-air, fire-water). At the four corners of the superimposed square are the four qualities defining the elements. Each adjacent pair of these is joined by a bar labeled "possible combination"; the diagonals joining them are labeled "impossible combination." Starting from the top, fire is formed from the combination of dryness and heat; air from wetness and heat; water from coldness and wetness; earth from coldness and dryness.
These four elements make up the four corners of a diamond (see picture to right). Opposing pairs of these are joined by a bar labeled "contraries" (earth-air, fire-water). At the four corners of the superimposed square are the four qualities defining the elements. Each adjacent pair of these is joined by a bar labeled "possible combination"; the diagonals joining them are labeled "impossible combination." Starting from the top, fire is formed from the combination of dryness and heat; air from wetness and heat; water from coldness and wetness; earth from coldness and dryness.
is a 2D geometric symbolic representation
of information
according to some visualization
technique. Sometimes, the technique uses a 3D visualization which is then projected
onto the 2D surface. The term diagram in common sense can have two meanings.
In science you will find the term used in both ways. For example Anderson (1997) stated more general "diagrams are pictorial, yet abstract, representations of information, and map
s, line graph
s, bar chart
s, engineering
blueprint
s, and architect
s' sketch
es are all examples of diagrams, whereas photographs and video are not". On the other hand Lowe (1993) defined diagrams as specifically "abstract graphic portrayals of the subject matter they represent".
In the specific sense diagrams and charts contrast computer graphics
, technical illustrations, infographics, maps, and technical drawing
s, by showing "abstract rather than literal
representations of information". The essences of a diagram can be seen as:
Or in Hall's (1996) words "diagrams are simplified figures, caricatures in a way, intended to convey essential meaning". According to Jan V. White (1984) "the characteristics of a good diagram are elegance, clarity, ease, pattern, simplicity, and validity". Elegance for White means that what you are seeing in the diagram is "the simplest and most fitting solution to a problem".
is a special type of graph-theoretic
structure in any one of several systems of graphical syntax
that Charles Sanders Peirce developed for logic
.
In his papers on qualitative logic, entitative graph
s, and existential graph
s, Peirce developed several versions of a graphical formalism
, or a graph-theoretic formal language
, designed to be interpreted for logic.
In the century since Peirce initiated this line of development, a variety of formal systems have branched out from what is abstractly the same formal base of graph-theoretic structures.
(CG) is a notation for logic based on the existential graph
s of Charles Sanders Peirce and the semantic network
s of artificial intelligence
. In the first published paper on conceptual graphs, John F. Sowa
used them to represent the conceptual schema
s used in database systems. His first book applied them to a wide range of topics in artificial intelligence, computer science, and cognitive science. A linear notation, called the Conceptual Graph Interchange Format (CGIF), has been standardized in the ISO standard for Common Logic
.
The diagram on the right is an example of the display form for a conceptual graph. Each box is called a concept node, and each oval is called a relation node. In CGIF, this CG would be represented by the following statement:
In CGIF, brackets enclose the information inside the concept nodes, and parentheses enclose the information inside the relation nodes. The letters x and y, which are called coreference labels, show how the concept and relation nodes are connected. In the Common Logic Interchange Format (CLIF), those letters are mapped to variables, as in the following statement:
As this example shows, the asterisks on the coreference labels *x and *y in CGIF map to existentially quantified variables in CLIF, and the question marks on ?x and ?y map to bound variables in CLIF. A universal quantifier, represented @every*z in CGIF, would be represented forall (z) in CLIF.
is an element of the graphical
syntax
for logic
that Charles Sanders Peirce developed under the name of qualitative logic beginning in the 1880s, taking the coverage of the formalism
only as far as the propositional or sentential
aspects of logic are concerned.
The syntax
is:
The semantics
are:
A "proof" manipulates a graph, using a short list of rules, until the graph is reduced to an empty cut or the blank page. A graph that can be so reduced is what is now called a tautology
(or the complement thereof). Graphs that cannot be simplified beyond a certain point are analogues of the satisfiable formula
s of first-order logic
.
is a type of diagram
matic or visual notation for logical expressions, proposed by Charles Sanders Peirce, who wrote his first paper on graphical logic
in 1882 and continued to develop the method until his death in 1914. Peirce proposed three systems of existential graphs:
Alpha nests in beta and gamma. Beta does not nest in gamma, quantified modal logic being more than even Peirce could envisage.
 In alpha the syntax
In alpha the syntax
is:
Any well-formed part of a graph is a subgraph.
The semantics
are:
Hence the alpha graphs are a minimalist notation for sentential logic, grounded in the expressive adequacy of And and Not. The alpha graphs constitute a radical simplification of the two-element Boolean algebra and the truth functors.
Depiction
Depiction is meaning conveyed through pictures. Basically, a picture maps an object to a two-dimensional scheme or picture plane. Pictures are made with various materials and techniques, such as painting, drawing, or prints mosaics, tapestries, stained glass, and collages of unusual and disparate...
s. The study of diagrammatic reasoning is about the understanding of concepts and ideas, visualized with the use of diagram
Diagram
A diagram is a two-dimensional geometric symbolic representation of information according to some visualization technique. Sometimes, the technique uses a three-dimensional visualization which is then projected onto the two-dimensional surface...
s and image
Image
An image is an artifact, for example a two-dimensional picture, that has a similar appearance to some subject—usually a physical object or a person.-Characteristics:...
ry instead of by linguistic
Natural language
In the philosophy of language, a natural language is any language which arises in an unpremeditated fashion as the result of the innate facility for language possessed by the human intellect. A natural language is typically used for communication, and may be spoken, signed, or written...
or algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
ic means.
Characteristica universalis
Characteristica universalisCharacteristica universalis
The Latin term characteristica universalis, commonly interpreted as universal characteristic, or universal character in English, is a universal and formal language imagined by the German philosopher Gottfried Leibniz able to express mathematical, scientific, and metaphysical concepts...
, commonly interpreted as universal characteristic, or universal character in English, is a universal and formal language imagined by the German philosopher Gottfried Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
able to express mathematical, scientific, and metaphysical concepts. Leibniz thus hoped to create a language usable within the framework of a universal logical calculation or calculus ratiocinator
Calculus ratiocinator
The Calculus Ratiocinator is a theoretical universal logical calculation framework, a concept described in the writings of Gottfried Leibniz, usually paired with his more frequently mentioned characteristica universalis, a universal conceptual language....
.
Since the characteristica universalis is diagrammatic and employs pictograms (below left), the diagrams in Leibniz's work warrant close study. On at least two occasions, Leibniz illustrated his philosophical reasoning with diagrams. One diagram, the frontispiece to his 1666 De Arte Combinatoria
De Arte Combinatoria
The Dissertatio de arte combinatoria is an early work by Gottfried Leibniz published in 1666 in Leipzig. It is an extended version of his doctoral dissertation, written before the author had seriously undertaken the study of mathematics. The booklet was reissued without Leibniz' consent in 1690,...
(On the Art of Combinations), represents the Aristotelian theory of how all material things are formed from combinations of the elements earth, water, air, and fire.

Diagram
A diagramDiagram
A diagram is a two-dimensional geometric symbolic representation of information according to some visualization technique. Sometimes, the technique uses a three-dimensional visualization which is then projected onto the two-dimensional surface...
is a 2D geometric symbolic representation
Depiction
Depiction is meaning conveyed through pictures. Basically, a picture maps an object to a two-dimensional scheme or picture plane. Pictures are made with various materials and techniques, such as painting, drawing, or prints mosaics, tapestries, stained glass, and collages of unusual and disparate...
of information
Information
Information in its most restricted technical sense is a message or collection of messages that consists of an ordered sequence of symbols, or it is the meaning that can be interpreted from such a message or collection of messages. Information can be recorded or transmitted. It can be recorded as...
according to some visualization
Illustration
An illustration is a displayed visualization form presented as a drawing, painting, photograph or other work of art that is created to elucidate or dictate sensual information by providing a visual representation graphically.- Early history :The earliest forms of illustration were prehistoric...
technique. Sometimes, the technique uses a 3D visualization which is then projected
3D projection
3D projection is any method of mapping three-dimensional points to a two-dimensional plane. As most current methods for displaying graphical data are based on planar two-dimensional media, the use of this type of projection is widespread, especially in computer graphics, engineering and drafting.-...
onto the 2D surface. The term diagram in common sense can have two meanings.

- visual information device: Like the term "illustrationIllustrationAn illustration is a displayed visualization form presented as a drawing, painting, photograph or other work of art that is created to elucidate or dictate sensual information by providing a visual representation graphically.- Early history :The earliest forms of illustration were prehistoric...
" the diagram is used as a collective term standing for the whole class of technical genres, including graphsGraphicsGraphics are visual presentations on some surface, such as a wall, canvas, computer screen, paper, or stone to brand, inform, illustrate, or entertain. Examples are photographs, drawings, Line Art, graphs, diagrams, typography, numbers, symbols, geometric designs, maps, engineering drawings,or...
, technical drawings and tableTable (information)A table is a means of arranging data in rows and columns.Production % of goalNorth 4087102%South 4093110% The use of tables is pervasive throughout all communication, research and data analysis. Tables appear in print media, handwritten notes, computer software, architectural...
s. - specific kind of visual display: This is only the genre, that shows qualitative data with shapes that are connected by lines, arrows, or other visual links.
In science you will find the term used in both ways. For example Anderson (1997) stated more general "diagrams are pictorial, yet abstract, representations of information, and map
Map
A map is a visual representation of an area—a symbolic depiction highlighting relationships between elements of that space such as objects, regions, and themes....
s, line graph
Line graph
In graph theory, the line graph L of undirected graph G is another graph L that represents the adjacencies between edges of G...
s, bar chart
Bar chart
A bar chart or bar graph is a chart with rectangular bars with lengths proportional to the values that they represent. The bars can be plotted vertically or horizontally....
s, engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
blueprint
Blueprint
A blueprint is a type of paper-based reproduction usually of a technical drawing, documenting an architecture or an engineering design. More generally, the term "blueprint" has come to be used to refer to any detailed plan....
s, and architect
Architect
An architect is a person trained in the planning, design and oversight of the construction of buildings. To practice architecture means to offer or render services in connection with the design and construction of a building, or group of buildings and the space within the site surrounding the...
s' sketch
Sketch (drawing)
A sketch is a rapidly executed freehand drawing that is not usually intended as a finished work...
es are all examples of diagrams, whereas photographs and video are not". On the other hand Lowe (1993) defined diagrams as specifically "abstract graphic portrayals of the subject matter they represent".
In the specific sense diagrams and charts contrast computer graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
, technical illustrations, infographics, maps, and technical drawing
Technical drawing
Technical drawing, also known as drafting or draughting, is the act and discipline of composing plans that visually communicate how something functions or has to be constructed.Drafting is the language of industry....
s, by showing "abstract rather than literal
Literal translation
Literal translation, or direct translation, is the rendering of text from one language to another "word-for-word" rather than conveying the sense of the original...
representations of information". The essences of a diagram can be seen as:
- a form of visual formatContent formatA content format is an encoded format for converting a specific type of data to displayable information. Content formats are used in recording and transmission to prepare data for observation or interpretation. This includes both analog and digitized content...
ting devices - a display that does not show quantitative data, but rather relationships and abstract information
- with building blocks such as geometrical shapes that are connected by lines, arrowArrowAn arrow is a shafted projectile that is shot with a bow. It predates recorded history and is common to most cultures.An arrow usually consists of a shaft with an arrowhead attached to the front end, with fletchings and a nock at the other.- History:...
s, or other visual links.
Or in Hall's (1996) words "diagrams are simplified figures, caricatures in a way, intended to convey essential meaning". According to Jan V. White (1984) "the characteristics of a good diagram are elegance, clarity, ease, pattern, simplicity, and validity". Elegance for White means that what you are seeing in the diagram is "the simplest and most fitting solution to a problem".
Logical graph
A logical graphLogical graph
A logical graph is a special type of diagramatic structure in any one of several systems of graphical syntax that Charles Sanders Peirce developed for logic....
is a special type of graph-theoretic
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
structure in any one of several systems of graphical syntax
Syntax (logic)
In logic, syntax is anything having to do with formal languages or formal systems without regard to any interpretation or meaning given to them...
that Charles Sanders Peirce developed for logic
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
.
In his papers on qualitative logic, entitative graph
Entitative graph
An entitative graph is an element of the diagrammatic syntax for logic that Charles Sanders Peirce developed under the name of qualitative logic beginning in the 1880's, taking the coverage of the formalism only as far as the propositional or sentential aspects of logic are concerned...
s, and existential graph
Existential graph
An existential graph is a type of diagrammatic or visual notation for logical expressions, proposed by Charles Sanders Peirce, who wrote on graphical logic as early as 1882, and continued to develop the method until his death in 1914.-The graphs:...
s, Peirce developed several versions of a graphical formalism
Formal system
In formal logic, a formal system consists of a formal language and a set of inference rules, used to derive an expression from one or more other premises that are antecedently supposed or derived . The axioms and rules may be called a deductive apparatus...
, or a graph-theoretic formal language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
, designed to be interpreted for logic.
In the century since Peirce initiated this line of development, a variety of formal systems have branched out from what is abstractly the same formal base of graph-theoretic structures.
Conceptual graph
A conceptual graphConceptual graph
Conceptual graphs are a formalism for knowledge representation. In the first published paper on CGs, John F. Sowa used them to represent the conceptual schemas used in database systems...
(CG) is a notation for logic based on the existential graph
Existential graph
An existential graph is a type of diagrammatic or visual notation for logical expressions, proposed by Charles Sanders Peirce, who wrote on graphical logic as early as 1882, and continued to develop the method until his death in 1914.-The graphs:...
s of Charles Sanders Peirce and the semantic network
Semantic network
A semantic network is a network which represents semantic relations among concepts. This is often used as a form of knowledge representation. It is a directed or undirected graph consisting of vertices, which represent concepts, and edges.- History :...
s of artificial intelligence
Artificial intelligence
Artificial intelligence is the intelligence of machines and the branch of computer science that aims to create it. AI textbooks define the field as "the study and design of intelligent agents" where an intelligent agent is a system that perceives its environment and takes actions that maximize its...
. In the first published paper on conceptual graphs, John F. Sowa
John F. Sowa
John Florian Sowa is the computer scientist who invented conceptual graphs, a graphic notation for logic and natural language, based on the structures in semantic networks and on the existential graphs of Charles S. Peirce. He is currently developing high-level "ontologies" for artificial...
used them to represent the conceptual schema
Conceptual schema
A conceptual schema or conceptual data model is a map of concepts and their relationships. This describes the semantics of an organization and represents a series of assertions about its nature...
s used in database systems. His first book applied them to a wide range of topics in artificial intelligence, computer science, and cognitive science. A linear notation, called the Conceptual Graph Interchange Format (CGIF), has been standardized in the ISO standard for Common Logic
Common logic
Common logic is a framework for a family of logic languages, based on first-order logic, intended to facilitate the exchange and transmission of knowledge in computer-based systems....
.
The diagram on the right is an example of the display form for a conceptual graph. Each box is called a concept node, and each oval is called a relation node. In CGIF, this CG would be represented by the following statement:
-
- [Cat Elsie] [Sitting *x] [Mat *y] (agent ?x Elsie) (location ?x ?y)
In CGIF, brackets enclose the information inside the concept nodes, and parentheses enclose the information inside the relation nodes. The letters x and y, which are called coreference labels, show how the concept and relation nodes are connected. In the Common Logic Interchange Format (CLIF), those letters are mapped to variables, as in the following statement:
-
- (exists ((x Sitting) (y Mat)) (and (Cat Elsie) (agent x Elsie) (location x y)))
As this example shows, the asterisks on the coreference labels *x and *y in CGIF map to existentially quantified variables in CLIF, and the question marks on ?x and ?y map to bound variables in CLIF. A universal quantifier, represented @every*z in CGIF, would be represented forall (z) in CLIF.
Entitative graph
An entitative graphEntitative graph
An entitative graph is an element of the diagrammatic syntax for logic that Charles Sanders Peirce developed under the name of qualitative logic beginning in the 1880's, taking the coverage of the formalism only as far as the propositional or sentential aspects of logic are concerned...
is an element of the graphical
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
syntax
Syntax
In linguistics, syntax is the study of the principles and rules for constructing phrases and sentences in natural languages....
for logic
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
that Charles Sanders Peirce developed under the name of qualitative logic beginning in the 1880s, taking the coverage of the formalism
Formal system
In formal logic, a formal system consists of a formal language and a set of inference rules, used to derive an expression from one or more other premises that are antecedently supposed or derived . The axioms and rules may be called a deductive apparatus...
only as far as the propositional or sentential
Propositional calculus
In mathematical logic, a propositional calculus or logic is a formal system in which formulas of a formal language may be interpreted as representing propositions. A system of inference rules and axioms allows certain formulas to be derived, called theorems; which may be interpreted as true...
aspects of logic are concerned.
The syntax
Syntax
In linguistics, syntax is the study of the principles and rules for constructing phrases and sentences in natural languages....
is:
- The blank page;
- Single letters, phrases;
- Objects (subgraphs) enclosed by a simple closed curve called a cut. A cut can be empty.
The semantics
Semantics
Semantics is the study of meaning. It focuses on the relation between signifiers, such as words, phrases, signs and symbols, and what they stand for, their denotata....
are:
- The blank page denotes False;
- Letters, phrases, subgraphs, and entire graphs can be True or False;
- To surround objects with a cut is equivalent to Boolean complementation. Hence an empty cut denotes Truth;
- All objects within a given cut are tacitly joined by disjunction.
A "proof" manipulates a graph, using a short list of rules, until the graph is reduced to an empty cut or the blank page. A graph that can be so reduced is what is now called a tautology
Tautology (logic)
In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
(or the complement thereof). Graphs that cannot be simplified beyond a certain point are analogues of the satisfiable formula
Formula
In mathematics, a formula is an entity constructed using the symbols and formation rules of a given logical language....
s of first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
.
Existential graph
An existential graphExistential graph
An existential graph is a type of diagrammatic or visual notation for logical expressions, proposed by Charles Sanders Peirce, who wrote on graphical logic as early as 1882, and continued to develop the method until his death in 1914.-The graphs:...
is a type of diagram
Diagram
A diagram is a two-dimensional geometric symbolic representation of information according to some visualization technique. Sometimes, the technique uses a three-dimensional visualization which is then projected onto the two-dimensional surface...
matic or visual notation for logical expressions, proposed by Charles Sanders Peirce, who wrote his first paper on graphical logic
Logical graph
A logical graph is a special type of diagramatic structure in any one of several systems of graphical syntax that Charles Sanders Peirce developed for logic....
in 1882 and continued to develop the method until his death in 1914. Peirce proposed three systems of existential graphs:
- alpha – isomorphicIsomorphismIn abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
to sentential logic and the two-element Boolean algebra; - beta – isomorphic to first-order logicFirst-order logicFirst-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
with identity, with all formulas closed; - gamma – (nearly) isomorphic to normal modal logicNormal modal logicIn logic, a normal modal logic is a set L of modal formulas such that L contains:* All propositional tautologies;* All instances of the Kripke schema: \Box\toand it is closed under:...
.
Alpha nests in beta and gamma. Beta does not nest in gamma, quantified modal logic being more than even Peirce could envisage.

Syntax
In linguistics, syntax is the study of the principles and rules for constructing phrases and sentences in natural languages....
is:
- The blank page;
- Single letters or phrases written anywhere on the page;
- Any graph may be enclosed by a simple closed curve called a cut or sep. A cut can be empty. Cuts can nest and concatenate at will, but must never intersect.
Any well-formed part of a graph is a subgraph.
The semantics
Semantics
Semantics is the study of meaning. It focuses on the relation between signifiers, such as words, phrases, signs and symbols, and what they stand for, their denotata....
are:
- The blank page denotes Truth;
- Letters, phrases, subgraphs, and entire graphs may be True or False;
- To enclose a subgraph with a cut is equivalent to logical negationNegationIn logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified...
or Boolean complementation. Hence an empty cut denotes False; - All subgraphs within a given cut are tacitly conjoined.
Hence the alpha graphs are a minimalist notation for sentential logic, grounded in the expressive adequacy of And and Not. The alpha graphs constitute a radical simplification of the two-element Boolean algebra and the truth functors.
The Venn-II reasoning system
In the early 1990s Sun-Joo Shin presented an extension of Existential Graphs called Venn-II. Syntax and semantics are given formally, together with a set of Rules of Transformation which are shown to be sound and complete. Proofs proceed by applying the rules (which remove or add syntactic elements to or from diagrams) sequentially. Venn-II is equivalent in expressive power to a first-order monadic language.See also
- Heuristics
- How to Solve ItHow to Solve ItHow to Solve It is a small volume by mathematician George Pólya describing methods of problem solving.- Four principles :How to Solve It suggests the following steps when solving a mathematical problem:...
- Natural deductionNatural deductionIn logic and proof theory, natural deduction is a kind of proof calculus in which logical reasoning is expressed by inference rules closely related to the "natural" way of reasoning...
- Pólya, GeorgeGeorge PólyaGeorge Pólya was a Hungarian mathematician. He was a professor of mathematics from 1914 to 1940 at ETH Zürich and from 1940 to 1953 at Stanford University. He made fundamental contributions to combinatorics, number theory, numerical analysis and probability theory...
- Propositional calculusPropositional calculusIn mathematical logic, a propositional calculus or logic is a formal system in which formulas of a formal language may be interpreted as representing propositions. A system of inference rules and axioms allows certain formulas to be derived, called theorems; which may be interpreted as true...
- Spatial-temporal reasoningSpatial-temporal reasoningSpatial–temporal reasoning is used in both the fields of psychology and computer science.-Spatial–temporal reasoning in psychology:Spatial-temporal reasoning is the ability to visualize spatial patterns and mentally manipulate them over a time-ordered sequence of spatial transformations.This...
- TrikonicTrikonicTrikonic, is a technique of triadic analysis-synthesis which has been developed by Gary Richmond based on the original idea of a possible applied science making three categorial distinctions, which philosopher Charles Sanders Peirce, its creator, called “Trichotomic.” Peirce introduces trichotomic...
- Visual reasoningVisual reasoningIn a frequently cited paper in the journal Science and later book Eugene S. Ferguson, a mechanical engineer and historian of technology, claims what many engineers and technologists take for granted: visual reasoning is a widely used tool used in creating technological artefacts. There is ample...
Further reading
- Gerard Allwein and Jon Barwise (ed.) (1996). Logical Reasoning with Diagrams. Oxford University Press.
- Michael Anderson, Peter Cheng, Volker Haarslev (Eds.) (2000). Theory and Application of Diagrams: First International Conference, Diagrams 2000. Edinburgh, Scotland, UK, September 1–3, 2000. Proceedings.
- Micheal Anderson and R. McCartney (2003). Diagram Processing: Computing with Diagrams. In: Artificial Intelligence, Volume 145 , Issue 1-2 , April, 2003.
- James Robert Brown (1999). Philosophy of Mathematics: An Introduction to the World of Proofs and Pictures. Routledge.
- Janice Glasgow, N. Hari Narayanan, and B. Chandrasekaran (ed) (1995). Diagrammatic Reasoning: Cognitive and Computational Perspectives. AAAI Press.
- Gem Stapleton A Survey of Reasoning Systems Based on Euler Diagrams. Electronic Notes in Theoretical Computer Science. 2005.
External links
- Diagrammatic Reasoning Site from the University of Hartford,Connecticut, USA
- Lecture about Universal Algebra and Diagrammatic Reasoning by John Baez, 3 Feb 2006.
- Homepage of Sun-Joo Shin.
- Visual Modeling Group at the University of Brighton, UK.

