
De Arte Combinatoria
Encyclopedia
The Dissertatio de arte combinatoria is an early work by Gottfried Leibniz published in 1666 in Leipzig
. It is an extended version of his doctoral dissertation, written before the author had seriously undertaken the study of mathematics. The booklet was reissued without Leibniz' consent in 1690, which prompted him to publish a brief explanatory notice in the Acta Eruditorum
. During the
following years he repeatedly expressed regrets about its being circulated as he considered it immature. Nevertheless it was a very original work and it provided the author the first glimpse of fame among the scholars of his time.
The main idea behind the text is that of an alphabet of human thought
, which is attributed to Descartes. All concepts are nothing but combinations of a relatively small number of simple concepts, just as words are combinations of letters. All truths may be expressed as appropriate combinations of concepts, which can in turn be decomposed into simple ideas, rendering
the analysis much easier. Therefore, this alphabet would provide a logic of invention, opposed to that of demonstration which was known so far. Since all sentences are composed of a subject and a predicate, one might
For this, Leibniz was inspired in the Ars Magna of Ramon Llull
, although he criticized this author because of the arbitrariness of his categories and his indexing.
Leibniz discusses in this work some combinatorial concepts. He had read Clavius' comments to the Tractatus de Sphaera of Sacrobosco, and some other contemporary works. He introduced the term variationes ordinis for the permutations, combinationes for the combinations of two elements, con3nationes (shorthand for conternationes) for those of three elements, etc. His general term for combinations was complexions. He found the formula
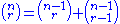
which he thought was original.
The first examples of use of his ars combinatoria are taken from law, the musical registry of an organ
, and the Aristotelian
theory of generation of elements from the four primary qualities. But philosophical applications are of greater importance. He cites the idea of Hobbes that all reasoning is just a computation.
The most careful example is taken from geometry, from where we shall give some definitions. He introduces the Class I concepts, which are primitive.
Class I: 1 point, 2 space, 3 included, [...] 9 parts, 10 total, [...] 14 number, 15 various [...]
Class II contains simple combinations.
Class II.1: Quantity is 14 των 9
Where των means "of the" (from ). Thus, "Quantity" is the number of the parts. Class III contains the con3nationes:
Class III.1: Interval is 2.3.10
Thus, "Interval" is the space included in total. Of course, concepts deriving from former classes may also be defined.
Class IV.1: Line is 1/3 των 2
Where 1/3 means the first concept of class III. Thus, a "line" is the interval of (between) points.
Leibniz compares his system to the Chinese and Egyptian languages, although he did not really understand them at this point. For him, this is a first step towards the Characteristica Universalis
, the perfect language which would provide a direct representation of ideas along with a calculus for the philosophical reasoning.
As a preface, the work begins with a proof of the existence of God, cast in geometrical form, and based on the Argument from Motion.
Leipzig
Leipzig Leipzig has always been a trade city, situated during the time of the Holy Roman Empire at the intersection of the Via Regia and Via Imperii, two important trade routes. At one time, Leipzig was one of the major European centres of learning and culture in fields such as music and publishing...
. It is an extended version of his doctoral dissertation, written before the author had seriously undertaken the study of mathematics. The booklet was reissued without Leibniz' consent in 1690, which prompted him to publish a brief explanatory notice in the Acta Eruditorum
Acta Eruditorum
Acta Eruditorum was the first scientific journal of the German lands, published from 1682 to 1782....
. During the
following years he repeatedly expressed regrets about its being circulated as he considered it immature. Nevertheless it was a very original work and it provided the author the first glimpse of fame among the scholars of his time.
The main idea behind the text is that of an alphabet of human thought
Alphabet of human thought
The alphabet of human thought is a concept originally proposed by Gottfried Leibniz that provides a universal way to represent and analyze ideas and relationships, no matter how complicated, by breaking down their component pieces...
, which is attributed to Descartes. All concepts are nothing but combinations of a relatively small number of simple concepts, just as words are combinations of letters. All truths may be expressed as appropriate combinations of concepts, which can in turn be decomposed into simple ideas, rendering
the analysis much easier. Therefore, this alphabet would provide a logic of invention, opposed to that of demonstration which was known so far. Since all sentences are composed of a subject and a predicate, one might
- Find all the predicates which are appropriate to a given subject, or
- Find all the subjects which are convenient to a given predicate.
For this, Leibniz was inspired in the Ars Magna of Ramon Llull
Ramon Llull
Ramon Llull was a Majorcan writer and philosopher, logician and tertiary Franciscan. He wrote the first major work of Catalan literature. Recently-surfaced manuscripts show him to have anticipated by several centuries prominent work on elections theory...
, although he criticized this author because of the arbitrariness of his categories and his indexing.
Leibniz discusses in this work some combinatorial concepts. He had read Clavius' comments to the Tractatus de Sphaera of Sacrobosco, and some other contemporary works. He introduced the term variationes ordinis for the permutations, combinationes for the combinations of two elements, con3nationes (shorthand for conternationes) for those of three elements, etc. His general term for combinations was complexions. He found the formula
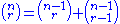
which he thought was original.
The first examples of use of his ars combinatoria are taken from law, the musical registry of an organ
Organ (music)
The organ , is a keyboard instrument of one or more divisions, each played with its own keyboard operated either with the hands or with the feet. The organ is a relatively old musical instrument in the Western musical tradition, dating from the time of Ctesibius of Alexandria who is credited with...
, and the Aristotelian
Aristotle
Aristotle was a Greek philosopher and polymath, a student of Plato and teacher of Alexander the Great. His writings cover many subjects, including physics, metaphysics, poetry, theater, music, logic, rhetoric, linguistics, politics, government, ethics, biology, and zoology...
theory of generation of elements from the four primary qualities. But philosophical applications are of greater importance. He cites the idea of Hobbes that all reasoning is just a computation.
The most careful example is taken from geometry, from where we shall give some definitions. He introduces the Class I concepts, which are primitive.
Class I: 1 point, 2 space, 3 included, [...] 9 parts, 10 total, [...] 14 number, 15 various [...]
Class II contains simple combinations.
Class II.1: Quantity is 14 των 9
Where των means "of the" (from ). Thus, "Quantity" is the number of the parts. Class III contains the con3nationes:
Class III.1: Interval is 2.3.10
Thus, "Interval" is the space included in total. Of course, concepts deriving from former classes may also be defined.
Class IV.1: Line is 1/3 των 2
Where 1/3 means the first concept of class III. Thus, a "line" is the interval of (between) points.
Leibniz compares his system to the Chinese and Egyptian languages, although he did not really understand them at this point. For him, this is a first step towards the Characteristica Universalis
Characteristica universalis
The Latin term characteristica universalis, commonly interpreted as universal characteristic, or universal character in English, is a universal and formal language imagined by the German philosopher Gottfried Leibniz able to express mathematical, scientific, and metaphysical concepts...
, the perfect language which would provide a direct representation of ideas along with a calculus for the philosophical reasoning.
As a preface, the work begins with a proof of the existence of God, cast in geometrical form, and based on the Argument from Motion.

