Determinantal variety
Encyclopedia
In algebraic geometry
, determinantal varieties are spaces of matrices with a given upper bound on their ranks. Their significance comes from the fact that many examples in algebraic geometry are of this form, such as the Segre embedding
of a product of two projective spaces.
as the condition that a matrix have rank ≤ r is given by the vanishing of all of its (r + 1) × (r + 1) minors
. Considering the generic m × n matrix whose entries are algebraically independent
variables x i,j, these minors are polynomials of degree r + 1. The ideal of k[x i,j] generated by these polynomials is a determinantal ideal. Since the equations defining minors are homogeneous, one can consider Y r either as an affine variety in mn-dimensional affine space
, or as a projective variety in (mn − 1)-dimensional projective space
.
Assuming that we consider Y r as an affine variety, its dimension is r(m + n − r). One way to see this is as follows: form the product space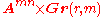
over 
where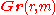 
is the Grassmannian
of r-planes in an m-dimensional vector space, and consider the subspace
, which is a desingularization
of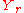
(over the open set of matrices with rank exactly r, this map is an isomorphism), and 
is a vector bundle over 
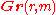which is isomorphic to 
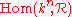where 
is the tautological bundle over the Grassmannian. So 
since they are birationally equivalent, and 
since the fiber of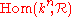 
has dimension nr.
The above shows that the matrices of rank <r contains the singular locus
of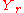
, and in fact one has equality. This fact can be verified using that the radical ideal is given by the minors along with the Jacobian criterion for nonsingularity.
The variety Y r naturally has an action of
, a product of general linear group
s. The problem of determining the syzygies
of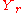
, when the characteristic
of the field is zero, was solved by Alain Lascoux
, using the natural action of G.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, determinantal varieties are spaces of matrices with a given upper bound on their ranks. Their significance comes from the fact that many examples in algebraic geometry are of this form, such as the Segre embedding
Segre embedding
In mathematics, the Segre embedding is used in projective geometry to consider the cartesian product of two or more projective spaces as a projective variety...
of a product of two projective spaces.
Definition
Given m and n and r < min(m, n), the determinantal variety Y r is the set of all m × n matrices (over a field k) with rank ≤ r. This is naturally an algebraic varietyAlgebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
as the condition that a matrix have rank ≤ r is given by the vanishing of all of its (r + 1) × (r + 1) minors
Minor (linear algebra)
In linear algebra, a minor of a matrix A is the determinant of some smaller square matrix, cut down from A by removing one or more of its rows or columns...
. Considering the generic m × n matrix whose entries are algebraically independent
Algebraic independence
In abstract algebra, a subset S of a field L is algebraically independent over a subfield K if the elements of S do not satisfy any non-trivial polynomial equation with coefficients in K...
variables x i,j, these minors are polynomials of degree r + 1. The ideal of k[x i,j] generated by these polynomials is a determinantal ideal. Since the equations defining minors are homogeneous, one can consider Y r either as an affine variety in mn-dimensional affine space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
, or as a projective variety in (mn − 1)-dimensional projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
.
Properties
The radical ideal defining the determinantal variety is generated by the (r + 1) × (r + 1) minors of the matrix (Bruns-Vetter, Theorem 2.10).Assuming that we consider Y r as an affine variety, its dimension is r(m + n − r). One way to see this is as follows: form the product space
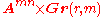over where 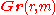is the GrassmannianGrassmannian
In mathematics, a Grassmannian is a space which parameterizes all linear subspaces of a vector space V of a given dimension. For example, the Grassmannian Gr is the space of lines through the origin in V, so it is the same as the projective space P. The Grassmanians are compact, topological...
of r-planes in an m-dimensional vector space, and consider the subspace
, which is a desingularizationResolution of singularities
In algebraic geometry, the problem of resolution of singularities asks whether every algebraic variety V has a resolution, a non-singular variety W with a proper birational map W→V...
of
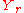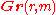(over the open set of matrices with rank exactly r, this map is an isomorphism), and is a vector bundle over which is isomorphic to 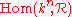where is the tautological bundle over the Grassmannian. So since they are birationally equivalent, and since the fiber of 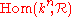has dimension nr.The above shows that the matrices of rank <r contains the singular locus
Singular point of an algebraic variety
In mathematics, a singular point of an algebraic variety V is a point P that is 'special' , in the geometric sense that V is not locally flat there. In the case of an algebraic curve, a plane curve that has a double point, such as the cubic curveexhibits at , cannot simply be parametrized near the...
of
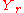, and in fact one has equality. This fact can be verified using that the radical ideal is given by the minors along with the Jacobian criterion for nonsingularity.The variety Y r naturally has an action of
, a product of general linear groupGeneral linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
s. The problem of determining the syzygies
Syzygy (mathematics)
In mathematics, a syzygy is a relation between the generators of a module M. The set of all such relations is called the "first syzygy module of M". A relation between generators of the first syzygy module is called a "second syzygy" of M, and the set of all such relations is called the...
of
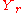, when the characteristicCharacteristic (algebra)
In mathematics, the characteristic of a ring R, often denoted char, is defined to be the smallest number of times one must use the ring's multiplicative identity element in a sum to get the additive identity element ; the ring is said to have characteristic zero if this repeated sum never reaches...
of the field is zero, was solved by Alain Lascoux
Alain Lascoux
Alain Lascoux is a French mathematician at the University of Marne la Vallée and Nankai University. His research fields include algebraic combinatorics, particuarly Hecke algebra and Young tableau....
, using the natural action of G.