
Bochner integral
Encyclopedia
In mathematics
, the Bochner integral, named for Salomon Bochner
, extends the definition of Lebesgue integral to functions that take values in a Banach space
, as the limit of integrals of simple function
s.
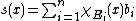
where the Ei are disjoint members of the σ-algebra Σ, the bi are distinct elements of B, and χE is the characteristic function
of E. If μ(Ei) is finite whenever bi ≠ 0, then the simple function is integrable, and the integral is then defined by

exactly as it is for the ordinary Lebesgue integral.
A measurable function ƒ : X → B is Bochner integrable if there exists a sequence of integrable simple functions sn such that
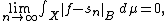
where the integral on the left-hand side is an ordinary Lebesgue integral.
In this case, the Bochner integral is defined by

It can be shown that a function is Bochner integrable if and only if it lies in the Bochner space
 .
.
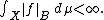
A function ƒ : X → B is called Bochner-measurable if it is equal μ-almost everywhere to a function g taking values in a separable subspace B0 of B, and such that the inverse image g−1(U) of every open set U in B belongs to Σ. Equivalently, ƒ is limit μ-almost everywhere of a sequence of simple functions.
A version of the dominated convergence theorem
also holds for the Bochner integral. Specifically, if ƒn : X → B is a sequence of measurable functions on a complete measure space tending almost everywhere to a limit function ƒ, and if
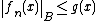
for almost every x ∈ X, and g ∈ L1(μ)
, then
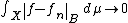
as n → ∞ and
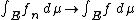
for all E ∈ Σ.
If ƒ is Bochner integrable, then the inequality
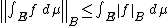
holds for all E ∈ Σ. In particular, the set function
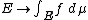
defines a countably-additive B-valued vector measure
on X which is absolutely continuous with respect to μ.
fails to hold in general. This results in an important property of Banach spaces known as the Radon–Nikodym property. Specifically, if μ is a measure on (X, Σ), then B has the Radon–Nikodym property with respect to μ if, for every countably-additive vector measure
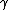 on (X, Σ) with values in B which has bounded variation and is absolutely continuous with respect to μ, there is a μ-integrable function g : X → B such that
on (X, Σ) with values in B which has bounded variation and is absolutely continuous with respect to μ, there is a μ-integrable function g : X → B such that
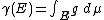
for every measurable set E ∈ Σ.
The Banach space B has the Radon–Nikodym property if B has the Radon–Nikodym property with respect to every finite measure. It is known that the space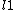
has the Radon–Nikodym property, but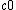 and the spaces
and the spaces 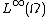 ,
, 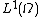 and
and 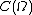 , for
, for 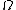 an open, bounded domain in
an open, bounded domain in 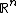 , do not. Spaces with Radon–Nikodym property include separable dual spaces (this is the Dunford–Pettis theorem) and reflexive space
, do not. Spaces with Radon–Nikodym property include separable dual spaces (this is the Dunford–Pettis theorem) and reflexive space
s, which include, in particular, Hilbert space
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Bochner integral, named for Salomon Bochner
Salomon Bochner
Salomon Bochner was an American mathematician of Austrian-Hungarian origin, known for wide-ranging work in mathematical analysis, probability theory and differential geometry.- Life :...
, extends the definition of Lebesgue integral to functions that take values in a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
, as the limit of integrals of simple function
Simple function
In the mathematical field of real analysis, a simple function is a real-valued function over a subset of the real line which attains only a finite number of values...
s.
Definition
Let (X, Σ, μ) be a measure space and B a Banach space. The Bochner integral is defined in much the same way as the Lebesgue integral. First, a simple function is any finite sum of the form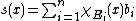
where the Ei are disjoint members of the σ-algebra Σ, the bi are distinct elements of B, and χE is the characteristic function
Characteristic function
In mathematics, characteristic function can refer to any of several distinct concepts:* The most common and universal usage is as a synonym for indicator function, that is the function* In probability theory, the characteristic function of any probability distribution on the real line is given by...
of E. If μ(Ei) is finite whenever bi ≠ 0, then the simple function is integrable, and the integral is then defined by

exactly as it is for the ordinary Lebesgue integral.
A measurable function ƒ : X → B is Bochner integrable if there exists a sequence of integrable simple functions sn such that
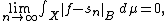
where the integral on the left-hand side is an ordinary Lebesgue integral.
In this case, the Bochner integral is defined by

It can be shown that a function is Bochner integrable if and only if it lies in the Bochner space
Bochner space
In mathematics, Bochner spaces are a generalization of the concept of Lp spaces to functions whose values lie in a Banach space which is not necessarily the space R or C of real or complex numbers....
 .
.Properties
Many of the familiar properties of the Lebesgue integral continue to hold for the Bochner integral. Perhaps the most striking example is Bochner's criterion for integrability, which states that if (X, Σ, μ) is a finite measure space, then a Bochner-measurable function ƒ : X → B is Bochner integrable if and only if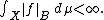
A function ƒ : X → B is called Bochner-measurable if it is equal μ-almost everywhere to a function g taking values in a separable subspace B0 of B, and such that the inverse image g−1(U) of every open set U in B belongs to Σ. Equivalently, ƒ is limit μ-almost everywhere of a sequence of simple functions.
A version of the dominated convergence theorem
Dominated convergence theorem
In measure theory, Lebesgue's dominated convergence theorem provides sufficient conditions under which two limit processes commute, namely Lebesgue integration and almost everywhere convergence of a sequence of functions...
also holds for the Bochner integral. Specifically, if ƒn : X → B is a sequence of measurable functions on a complete measure space tending almost everywhere to a limit function ƒ, and if
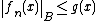
for almost every x ∈ X, and g ∈ L1(μ)
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
, then
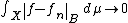
as n → ∞ and
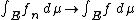
for all E ∈ Σ.
If ƒ is Bochner integrable, then the inequality
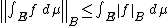
holds for all E ∈ Σ. In particular, the set function
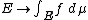
defines a countably-additive B-valued vector measure
Vector measure
In mathematics, a vector measure is a function defined on a family of sets and taking vector values satisfying certain properties. It is a generalization of the concept of measure, which takes nonnegative real values only.-Definitions and first consequences:...
on X which is absolutely continuous with respect to μ.
Radon–Nikodym property
An important fact about the Bochner integral is that the Radon–Nikodym theoremRadon–Nikodym theorem
In mathematics, the Radon–Nikodym theorem is a result in measure theory that states that, given a measurable space , if a σ-finite measure ν on is absolutely continuous with respect to a σ-finite measure μ on , then there is a measurable function f on X and taking values in [0,∞), such that\nu =...
fails to hold in general. This results in an important property of Banach spaces known as the Radon–Nikodym property. Specifically, if μ is a measure on (X, Σ), then B has the Radon–Nikodym property with respect to μ if, for every countably-additive vector measure
Vector measure
In mathematics, a vector measure is a function defined on a family of sets and taking vector values satisfying certain properties. It is a generalization of the concept of measure, which takes nonnegative real values only.-Definitions and first consequences:...
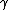 on (X, Σ) with values in B which has bounded variation and is absolutely continuous with respect to μ, there is a μ-integrable function g : X → B such that
on (X, Σ) with values in B which has bounded variation and is absolutely continuous with respect to μ, there is a μ-integrable function g : X → B such that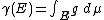
for every measurable set E ∈ Σ.
The Banach space B has the Radon–Nikodym property if B has the Radon–Nikodym property with respect to every finite measure. It is known that the space
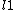
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
has the Radon–Nikodym property, but
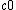 and the spaces
and the spaces 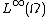 ,
, 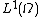 and
and 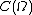 , for
, for 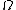 an open, bounded domain in
an open, bounded domain in 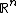 , do not. Spaces with Radon–Nikodym property include separable dual spaces (this is the Dunford–Pettis theorem) and reflexive space
, do not. Spaces with Radon–Nikodym property include separable dual spaces (this is the Dunford–Pettis theorem) and reflexive spaceReflexive space
In functional analysis, a Banach space is called reflexive if it coincides with the dual of its dual space in the topological and algebraic senses. Reflexive Banach spaces are often characterized by their geometric properties.- Normed spaces :Suppose X is a normed vector space over R or C...
s, which include, in particular, Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
s.

