Complex polygon
Encyclopedia
The term complex polygon can mean two different things:
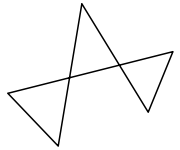In the world of computer graphics, a complex polygon is a polygon
which is neither convex
nor concave. This includes any polygon which:
Therefore, unlike simple polygon
s, a complex polygon may not always be interpreted as a simple polygonal region. Vertices are only counted at the ends of edges, not where edges intersect in space.
A formula relating an integral over a bounded region to a closed line integral
may still apply when the "inside-out" parts of the region are counted negatively.
Moving around the polygon, the total amount one "turns" at the vertices can be any integer times 360°, e.g. 720° for a pentagram
and 0° for an angular "eight".
See also: orbit (dynamics)
, Winding number
.
, a complex polygon is a polygon in the complex Hilbert
plane, which has two complex
dimensions.
A complex number
may be represented in the form
, where 
and 
are real number
s, and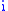
is the square root of 
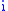. A complex number lies in a complex plane
having one real and one imaginary dimension, which may be represented as an Argand diagram. So a single complex dimension is really two dimensions, but of different kinds.
The unitary plane comprises two such complex planes, which are orthogonal to each other. Thus it has two real dimensions
and 
and two imaginary dimensions 
and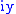 
.
A complex polygon is a two-dimensional example of the more general complex polytope
in higher dimensions.
In a real plane, a visible figure can be constructed as the real conjugate of some complex polygon.
- In computer graphicsComputer graphicsComputer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
, as a polygonPolygonIn geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
which is neither convexConvex polygonIn geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...
nor concave. - In geometryGeometryGeometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, as a polygon in the unitary plane, which has two complexComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
dimensions.
Computer graphics
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
which is neither convex
Convex polygon
In geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...
nor concave. This includes any polygon which:
- Intersects itself. These include star polygons such as the pentagramPentagramA pentagram is the shape of a five-pointed star drawn with five straight strokes...
:
- Has a boundary comprising discrete circuits, such as a polygon with a hole in it.
Therefore, unlike simple polygon
Simple polygon
In geometry, a simple polygon is a closed polygonal chain of line segments in the plane which do not have points in common other than the common vertices of pairs of consecutive segments....
s, a complex polygon may not always be interpreted as a simple polygonal region. Vertices are only counted at the ends of edges, not where edges intersect in space.
A formula relating an integral over a bounded region to a closed line integral
Line integral
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...
may still apply when the "inside-out" parts of the region are counted negatively.
Moving around the polygon, the total amount one "turns" at the vertices can be any integer times 360°, e.g. 720° for a pentagram
Pentagram
A pentagram is the shape of a five-pointed star drawn with five straight strokes...
and 0° for an angular "eight".
See also: orbit (dynamics)
Orbit (dynamics)
In mathematics, in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the...
, Winding number
Winding number
In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...
.
Geometry
In geometryGeometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a complex polygon is a polygon in the complex Hilbert
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
plane, which has two complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
dimensions.
A complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
may be represented in the form
, where and are real numberReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, and
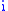is the square root of 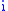. A complex number lies in a complex planeComplex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
having one real and one imaginary dimension, which may be represented as an Argand diagram. So a single complex dimension is really two dimensions, but of different kinds.
The unitary plane comprises two such complex planes, which are orthogonal to each other. Thus it has two real dimensions
and and two imaginary dimensions and 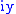.A complex polygon is a two-dimensional example of the more general complex polytope
Complex polytope
A complex polytope is a generalization of a polytope in real space to an analogous structure in a complex Hilbert space, where each real dimension is accompanied by an imaginary one....
in higher dimensions.
In a real plane, a visible figure can be constructed as the real conjugate of some complex polygon.
See also
- Simple polygonSimple polygonIn geometry, a simple polygon is a closed polygonal chain of line segments in the plane which do not have points in common other than the common vertices of pairs of consecutive segments....
- Convex and concave polygons
- Star polygon
- Convex hullConvex hullIn mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
- Nonconvex uniform polyhedronNonconvex uniform polyhedronIn geometry, a uniform star polyhedron is a self-intersecting uniform polyhedron. They are also sometimes called nonconvex polyhedra to imply self-intersecting...