
Curve of constant width
Encyclopedia
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a curve of constant width is a convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
planar shape
Shape
The shape of an object located in some space is a geometrical description of the part of that space occupied by the object, as determined by its external boundary – abstracting from location and orientation in space, size, and other properties such as colour, content, and material...
whose width, defined as the perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
distance between two distinct parallel lines each intersecting its boundary in a single point, is the same regardless of the direction of those two parallel lines.
More generally, any compact convex planar body D has one pair of parallel supporting line
Supporting line
In geometry, a supporting line L of a curve C in the plane is a line that contains a point of C, but does not separate any two points of C. In other words, C lies completely in one of the two closed half-planes defined by L and has at least one point on L.There can be many supporting lines for a...
s in any given direction. A supporting line
Supporting line
In geometry, a supporting line L of a curve C in the plane is a line that contains a point of C, but does not separate any two points of C. In other words, C lies completely in one of the two closed half-planes defined by L and has at least one point on L.There can be many supporting lines for a...
is a line that has at least one point in common with the boundary of D but no points in common with the interior of D. The width of the body is defined as before. If the width of D is the same in all directions, the body is said to have constant width and its boundary is a curve of constant width; the planar body itself is called an orbiform.
The width of a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
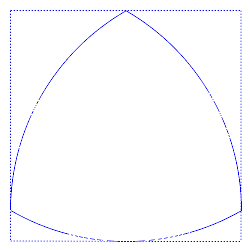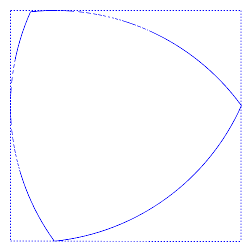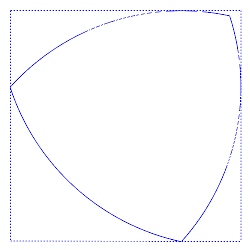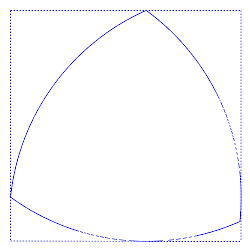
is constant: its diameter. The width of a square varies between the length of a side and that of a diagonal, in the ratio 1:√2. Thus the question arises: if a given shape's width is constant in all directions, is it necessarily a circle? The surprising answer is that there are many non-circular shapes of constant width. A nontrivial example is the Reuleaux triangle
Reuleaux triangle
A Reuleaux triangle is, apart from the trivial case of the circle, the simplest and best known Reuleaux polygon, a curve of constant width. The separation of two parallel lines tangent to the curve is independent of their orientation...
. To construct this, take an equilateral triangle with vertices ABC and draw the arc BC on the circle centered at A, the arc CA on the circle centered at B, and the arc AB on the circle centered at C. The resulting figure is of constant width.
The Reuleaux triangle lacks tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
continuity at three points, but constant-width curves can also be constructed without such discontinuities (as shown in the second illustration at right). Curves of constant width can be generated by joining circular arcs centered on the vertices of a regular or irregular convex polygon with an odd number of sides (triangle, pentagon, heptagon, etc.).
Properties
Curves of constant width can be rotated between parallel line segments. To see this, simply note that one can rotate parallel line segments (supporting lines) around curves of constant width by definition.Consequently, a curve of constant width can be rotated in a square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
.
A basic result on curves of constant width is Barbier's theorem
Barbier's theorem
Barbier's theorem, a basic result on curves of constant width first proved by Joseph Emile Barbier, states that the perimeter of any curve of constant width w is πw....
, which asserts that the perimeter
Perimeter
A perimeter is a path that surrounds an area. The word comes from the Greek peri and meter . The term may be used either for the path or its length - it can be thought of as the length of the outline of a shape. The perimeter of a circular area is called circumference.- Practical uses :Calculating...
of any curve of constant width is equal to the width (diameter
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
) multiplied by π. A simple example of this would be a circle with width (diameter
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
) d having a perimeter of πd.
By the isoperimetric inequality and Barbier's theorem, the circle has the maximum area of any curve of given constant width. The Blaschke-Lebesgue theorem says that the Reuleaux triangle has the least area of any curve of given constant width.
Applications
A wheel rotating around a fixed axle must be circular in shape to allow smooth forward motion; however, a loose "roller" does not have to be circular in shape to allow smooth forward motion (without any vertical bumpiness) — any curve of constant width will do. Therefore if flat material is placed on two or more rollers (in the shape of curves of the same constant width) resting on a flat surface, the material will remain a constant height off the ground as it is pushed forward (though the rollers themselves will appear to "move in a curiously irregular manner" if their shape is significantly non-circular).Curves of constant width are also the general answer to a brain teaser
Brain teaser
A brain teaser is a form of puzzle that requires thought to solve. It often requires thinking in unconventional ways with given constraints in mind; sometimes it also involves lateral thinking. Logic puzzles and riddles are specific types of brain teasers....
: "What shape can you make a manhole cover
Manhole cover
A manhole cover is a removable plate forming the lid over the opening of a manhole, to prevent anyone from falling in and to keep unauthorized persons out....
so that it cannot fall down through the hole?" In practice, there is no compelling reason to make manhole covers non-circular. Circles are easier to machine, and need not be rotated to a particular alignment in order to seal the hole.
Generalizations
Δ curves, which can be rotated in the equilateral triangle, have many similar properties to curves of constant width.The generalization of the definition of bodies of constant width to convex bodies in R³ and their boundaries leads to the concept of surface of constant width
Surface of constant width
In geometry, a surface of constant width is a convex form whose width, measured by the distance between two opposite parallelplanes touching its boundary, is the same regardless of the direction of those two parallel planes. One defines the width of the surface in a given direction to be the...
(in the case of a Reuleaux triangle
Reuleaux triangle
A Reuleaux triangle is, apart from the trivial case of the circle, the simplest and best known Reuleaux polygon, a curve of constant width. The separation of two parallel lines tangent to the curve is independent of their orientation...
, this does not lead to a Reuleaux tetrahedron
Reuleaux tetrahedron
The Reuleaux tetrahedron is the intersection of four spheres of radius s centered at the vertices of a regular tetrahedron with side length s. The sphere through each vertex passes through the other three vertices, which also form vertices of the Reuleaux tetrahedron...
, but to Meissner bodies). There is also the concept of space curves of constant width, whose widths are defined by tangent planes.
Examples
Famous examples of a curve of constant width are the British 20p and 50p coins. Their heptagonal shape with curved sides means that the currency detectorCurrency detector
A currency detector is a device that determines if a piece of currency is, or is not, counterfeit. These devices are used in vending machines that accept payment and dispense a product to a customer...
in an automated coin machine will always measure the same width, no matter which angle it takes its measurement from.
There exists a polynomial
 of degree 8, whose graph (i.e., set of points in
of degree 8, whose graph (i.e., set of points in  for which
for which  ) is a non-circular curve of constant width.http://www.mathpropress.com/stan/bibliography/polynomialConstantWidth.pdf
) is a non-circular curve of constant width.http://www.mathpropress.com/stan/bibliography/polynomialConstantWidth.pdfExternal links
- How round is your circle? contains a chapter on this topic.
- Animated Java applet by Michael Borcherds showing an irregular shape of constant width (that you can change) made using GeoGebra.
- Star Construction of Shapes of Constant Width at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Weisstein, Eric W. "Curve of Constant Width." From MathWorld--A Wolfram Web Resource.
- Multi-angle-wheel bicycle appears in Qingdao - bicycle with wheels using this property.

