
Reuleaux triangle
Encyclopedia

Curve of constant width
In geometry, a curve of constant width is a convex planar shape whose width, defined as the perpendicular distance between two distinct parallel lines each intersecting its boundary in a single point, is the same regardless of the direction of those two parallel lines.More generally, any compact...
. The separation of two parallel lines tangent to the curve is independent of their orientation. The term derives from Franz Reuleaux
Franz Reuleaux
Franz Reuleaux , was a mechanical engineer and a lecturer of the Berlin Royal Technical Academy, later appointed as the President of the Academy. He was often called the father of kinematics...
, a 19th-century German engineer who did pioneering work on ways that machines translate one type of motion into another, although the concept was known before his time.
Construction
With a compassCompass (drafting)
A compass or pair of compasses is a technical drawing instrument that can be used for inscribing circles or arcs. As dividers, they can also be used as a tool to measure distances, in particular on maps...
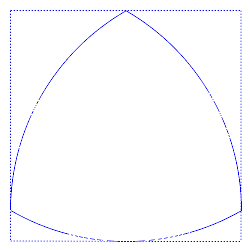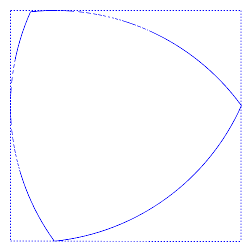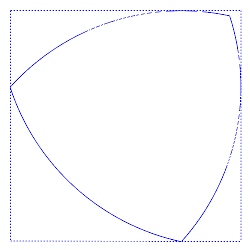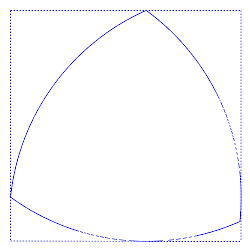
, sweep an arc sufficient to enclose the desired figure. With radius unchanged, sweep a sufficient arc centred at a point on the first arc to intersect that arc. With the same radius and the centre at that intersection sweep a third arc to intersect the other arcs. The result is a curve of constant width. Because all diameters are the same, the Reuleaux triangle is an answer to the question "Other than a circle, what shape can a manhole cover
Manhole cover
A manhole cover is a removable plate forming the lid over the opening of a manhole, to prevent anyone from falling in and to keep unauthorized persons out....
be made so that it cannot fall down through the hole?"
Equivalently, given an equilateral triangle T of side length s, take the boundary of the intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of the disks with radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
s centered at the vertices of T.
By the Blaschke-Lebesgue theorem, the Reuleaux triangle has the least area of any curve of given constant width. This area is
 , where s is the constant width. The existence of Reuleaux polygons shows that diameter measurements alone cannot verify that an object has a circular cross-section.
, where s is the constant width. The existence of Reuleaux polygons shows that diameter measurements alone cannot verify that an object has a circular cross-section.The area of Reuleaux triangle is smaller than that of the disk
Disk (mathematics)
In geometry, a disk is the region in a plane bounded by a circle.A disk is said to be closed or open according to whether or not it contains the circle that constitutes its boundary...
of the same width (ie diameter); the area of such a disk is
 .
.Reuleaux polygons
The Reuleaux triangle can be generalized to regular polygonRegular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
s with an odd number of sides, yielding a Reuleaux polygon. The most commonly used of these is the Reuleaux heptagon, which is the shape of several coins:
- BritishUnited KingdomThe United Kingdom of Great Britain and Northern IrelandIn the United Kingdom and Dependencies, other languages have been officially recognised as legitimate autochthonous languages under the European Charter for Regional or Minority Languages...
twenty pence and fifty pence. - Botswana pulaBotswana pulaThe pula is the currency of Botswana. It has the ISO 4217 code BWP and is subdivided into 100 thebe. Pula literally means "rain" in Setswana, because rain is very scarce in Botswana - home to much of the Kalahari Desert - and therefore valuable. Pula also means "blessing" as rain is considered a...
coins in the denominations of 2 Pula, 1 Pula, 25 Thebe and 5 Thebe. - Cypriot 50 cent coin, from 1991 until Cyprus joined the EuroEuroThe euro is the official currency of the eurozone: 17 of the 27 member states of the European Union. It is also the currency used by the Institutions of the European Union. The eurozone consists of Austria, Belgium, Cyprus, Estonia, Finland, France, Germany, Greece, Ireland, Italy, Luxembourg,...
in 2008.
The constant width of such coins allows their use in coin-operated machines.
Other uses
- The rotor of the Wankel engineWankel engineThe Wankel engine is a type of internal combustion engine using an eccentric rotary design to convert pressure into a rotating motion instead of using reciprocating pistons. Its four-stroke cycle takes place in a space between the inside of an oval-like epitrochoid-shaped housing and a rotor that...
is easily mistaken for a Reuleaux triangle but its curved sides are somewhat flatter than those of a Reuleaux triangle and so it does not have constant width.
- The Harry Watt square drill bitDrill bitDrill bits are cutting tools used to create cylindrical holes. Bits are held in a tool called a drill, which rotates them and provides torque and axial force to create the hole. Specialized bits are also available for non-cylindrical-shaped holes....
has the shape of a Reuleaux triangle and can, if mounted in a special chuck which allows for the bit not having a fixed centre of rotation, drill a hole that is nearly square. The Harry Watt square is often used in mortisingMortiserA mortiser or morticer is a specialized woodworking machine used to cut square or rectangular holes in a piece of lumber, such as a mortise in a mortise and tenon joint.-Square chisel mortiser:...
Other Reuleaux polygons are used to drill pentagonal, hexagonal, and octagonal holes.
- A Reuleaux triangle (along with all other curves of constant widthCurve of constant widthIn geometry, a curve of constant width is a convex planar shape whose width, defined as the perpendicular distance between two distinct parallel lines each intersecting its boundary in a single point, is the same regardless of the direction of those two parallel lines.More generally, any compact...
) can roll but makes a poor wheel because it does not roll about a fixed center of rotation. An object on top of rollers with cross-sections that were Reuleaux triangles would roll smoothly and flatly, but an axle attached to Reuleaux triangle wheels would bounce up and down three times per revolution. This concept was used in a science fiction short story by Poul AndersonPoul AndersonPoul William Anderson was an American science fiction author who began his career during one of the Golden Ages of the genre and continued to write and remain popular into the 21st century. Anderson also authored several works of fantasy, historical novels, and a prodigious number of short stories...
titled "The Three-Cornered Wheel."
- Several pencils are manufactured in this shape, rather than the more traditional round or hexagonal barrels. They are usually promoted as being more comfortable or encouraging proper grip, as well as being less likely to roll off tables.
- The shape is used for signage for the National Trails SystemNational Trails SystemThe National Trails System was created by the National Trails System Act The Act created a series of National trails "to promote the preservation of, public access to, travel within, and enjoyment and appreciation of the open-air, outdoor areas and historic resources of the Nation." Specifically,...
administered by the United States National Park Service, as well as the logo of Colorado School of MinesColorado School of MinesThe Colorado School of Mines is a small public teaching and research university devoted to engineering and applied science, with special expertise in the development and stewardship of the Earth's natural resources. Located in Golden, Colorado, CSM was ranked 29th, in America among national...
.
- Valve covers used in the Mission Bay Project of San Francisco to differentiate reclaimed water from potable water are in the shape of a Reuleaux triangle.
Three-dimensional version
The intersection of four spheres of radius s centered at the vertices of a regular tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
with side length s is called the Reuleaux tetrahedron
Reuleaux tetrahedron
The Reuleaux tetrahedron is the intersection of four spheres of radius s centered at the vertices of a regular tetrahedron with side length s. The sphere through each vertex passes through the other three vertices, which also form vertices of the Reuleaux tetrahedron...
, but is not a surface of constant width
Surface of constant width
In geometry, a surface of constant width is a convex form whose width, measured by the distance between two opposite parallelplanes touching its boundary, is the same regardless of the direction of those two parallel planes. One defines the width of the surface in a given direction to be the...
. It can, however, be made into a surface of constant width, called Meissner's tetrahedron, by replacing its edge arcs by curved surface patches. Alternatively, the surface of revolution
Surface of revolution
A surface of revolution is a surface in Euclidean space created by rotating a curve around a straight line in its plane ....
of a Reuleaux triangle through one of its symmetry axes forms a surface of constant width, with minimum volume among all known surfaces of revolution of given constant width .
See also
- Deltoid curveDeltoid curveIn geometry, a deltoid, also known as a tricuspoid or Steiner curve, is a hypocycloid of three cusps. In other words, it is the roulette created by a point on the circumference of a circle as it rolls without slipping along the inside of a circle with three times its radius...
- SuperellipseSuperellipseA superellipse is a geometric figure defined in the Cartesian coordinate system as the set of all points withwhere n, a and b are positive numbers....
- Vesica piscisVesica piscisThe vesica piscis is a shape that is the intersection of two circles with the same radius, intersecting in such a way that the center of each circle lies on the circumference of the other. The name literally means the "bladder of a fish" in Latin...
- Watts Brothers Tool WorksWatts Brothers Tool WorksWatts Brothers Tool Works is a tool manufacturer located in Wilmerding, Pennsylvania, USA. They are known for manufacturing drill bits which can drill square holes, including blind holes which cannot be made with other methods such as broaching...
External links
- How Round is Your Circle? - book about various geometric properties, including curves and solids of constant width
- Shapes of constant width at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Downloadable film about the Reuleaux triangle, also showing the Wankel engine and the mechanics of a Soviet film projector

