
Reuleaux tetrahedron
Encyclopedia
The Reuleaux tetrahedron is the intersection of four spheres of radius
s centered at the vertices
of a regular tetrahedron
with side length s. The sphere through each vertex passes through the other three vertices, which also form vertices of the Reuleaux tetrahedron. The Reuleaux tetrahedron has the same face structure as a regular tetrahedron, but with curved faces: four vertices, and four curved faces, connected by six circular-arc edges.
This shape is defined and named by analogy to the Reuleaux triangle
, a two-dimensional curve of constant width
. One can find repeated claims in the mathematical literature that the Reuleaux tetrahedron is analogously a surface of constant width
, but it is not true: the two midpoints of opposite edge arcs are separated by a larger distance,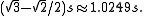
The volume of a Reuleaux tetrahedron is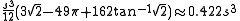
, by replacing three of its edge arcs by curved patches formed as the surfaces of rotation of a circular arc. According to which three edge arcs are replaced (three that have a common vertex or three that form a triangle) there result two noncongruent shapes that are sometimes called Meissner bodies or Meissner tetrahedra (pictures and films in Weber 2009). Bonnesen and Fenchel conjectured that Meissner tetrahedra are the minimum-volume three-dimensional shapes of constant width, a conjecture which is still open. In connection with this problem, Campi, Colesanti and Gronchi showed that the minimum volume surface of revolution with constant width is the surface of revolution of a Reuleaux triangle through one of its symmetry axes.
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
s centered at the vertices
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
of a regular tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
with side length s. The sphere through each vertex passes through the other three vertices, which also form vertices of the Reuleaux tetrahedron. The Reuleaux tetrahedron has the same face structure as a regular tetrahedron, but with curved faces: four vertices, and four curved faces, connected by six circular-arc edges.
This shape is defined and named by analogy to the Reuleaux triangle
Reuleaux triangle
A Reuleaux triangle is, apart from the trivial case of the circle, the simplest and best known Reuleaux polygon, a curve of constant width. The separation of two parallel lines tangent to the curve is independent of their orientation...
, a two-dimensional curve of constant width
Curve of constant width
In geometry, a curve of constant width is a convex planar shape whose width, defined as the perpendicular distance between two distinct parallel lines each intersecting its boundary in a single point, is the same regardless of the direction of those two parallel lines.More generally, any compact...
. One can find repeated claims in the mathematical literature that the Reuleaux tetrahedron is analogously a surface of constant width
Surface of constant width
In geometry, a surface of constant width is a convex form whose width, measured by the distance between two opposite parallelplanes touching its boundary, is the same regardless of the direction of those two parallel planes. One defines the width of the surface in a given direction to be the...
, but it is not true: the two midpoints of opposite edge arcs are separated by a larger distance,
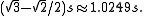
The volume of a Reuleaux tetrahedron is
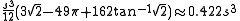
Meissner bodies
Meissner and Schilling showed how to modify the Reuleaux tetrahedron to form a surface of constant widthSurface of constant width
In geometry, a surface of constant width is a convex form whose width, measured by the distance between two opposite parallelplanes touching its boundary, is the same regardless of the direction of those two parallel planes. One defines the width of the surface in a given direction to be the...
, by replacing three of its edge arcs by curved patches formed as the surfaces of rotation of a circular arc. According to which three edge arcs are replaced (three that have a common vertex or three that form a triangle) there result two noncongruent shapes that are sometimes called Meissner bodies or Meissner tetrahedra (pictures and films in Weber 2009). Bonnesen and Fenchel conjectured that Meissner tetrahedra are the minimum-volume three-dimensional shapes of constant width, a conjecture which is still open. In connection with this problem, Campi, Colesanti and Gronchi showed that the minimum volume surface of revolution with constant width is the surface of revolution of a Reuleaux triangle through one of its symmetry axes.

