
Cubic plane curve
Encyclopedia
In mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a cubic plane curve is a plane algebraic curve C defined by a cubic equation
- F(x,y,z) = 0
applied to homogeneous coordinates
Homogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
x:y:z for the projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
; or the inhomogeneous version for the affine space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
determined by setting z = 1 in such an equation. Here F is a non-zero linear combination of the third-degree monomial
Monomial
In mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
s
- x3, y3, z3, x2y, x2z, y2x, y2z, z2x, z2y, xyz.
These are ten in number; therefore the cubic curves form a projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
of dimension 9, over any given field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K. Each point P imposes a single linear condition on F, if we ask that C pass through P. Therefore we can find some cubic curve through any nine given points, which may be degenerate, and may not be unique, but will be unique and non-degenerate if the points are in general position
General position
In algebraic geometry, general position is a notion of genericity for a set of points, or other geometric objects. It means the general case situation, as opposed to some more special or coincidental cases that are possible...
; compare to two points determining a line and how five points determine a conic
Five points determine a conic
In geometry, just as two points determine a line , five points determine a conic . There are additional subtleties for conics that do not exist for lines, and thus the statement and its proof for conics are both more technical than for lines.Formally, given any five points in the plane in general...
. If two cubics pass through a given set of nine points, then in fact a pencil
Pencil (mathematics)
A pencil in projective geometry is a family of geometric objects with a common property, for example the set of lines that pass through a given point in a projective plane....
of cubics does, and the points satisfy additional properties; see Cayley–Bacharach theorem.
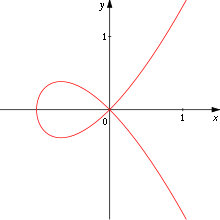
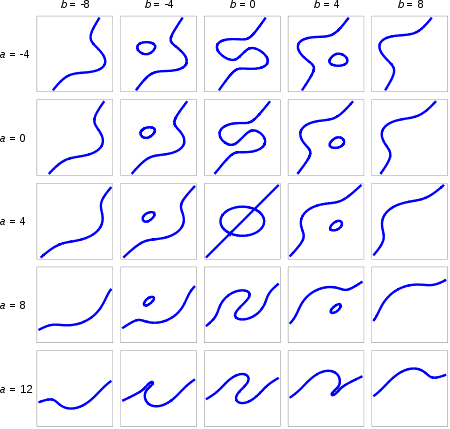
Mathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
; in which case it has a parametrization in terms of a projective line
Projective line
In mathematics, a projective line is a one-dimensional projective space. The projective line over a field K, denoted P1, may be defined as the set of one-dimensional subspaces of the two-dimensional vector space K2 .For the generalisation to the projective line over an associative ring, see...
. Otherwise a non-singular cubic curve is known to have nine points of inflection
Inflection point
In differential calculus, an inflection point, point of inflection, or inflection is a point on a curve at which the curvature or concavity changes sign. The curve changes from being concave upwards to concave downwards , or vice versa...
, over an algebraically closed field such as the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s. This can be shown by taking the homogeneous version of the Hessian matrix
Hessian matrix
In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
, which defines again a cubic, and intersecting it with C; the intersections are then counted by Bézout's theorem
Bézout's theorem
Bézout's theorem is a statement in algebraic geometry concerning the number of common points, or intersection points, of two plane algebraic curves. The theorem claims that the number of common points of two such curves X and Y is equal to the product of their degrees...
. These points cannot however all be real, so that they cannot be seen in the real projective plane by drawing the curve. The real points of cubic curves were studied by Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
; they fall into one or two 'ovals'.
A non-singular cubic defines an elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
, over any field K for which it has a point defined. Elliptic curves are now normally studied in some variant of Weierstrass's elliptic functions
Weierstrass's elliptic functions
In mathematics, Weierstrass's elliptic functions are elliptic functions that take a particularly simple form; they are named for Karl Weierstrass...
, defining a quadratic extension of the field of rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s made by extracting the square root of a cubic. This does depend on having a K-rational point, which serves as the point at infinity in Weierstrass form. For example, there are many cubic curves that have no such point, when K is the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
field.
The singular points of an irreducible plane cubic curve are quite limited: one double point, or one cusp
Cusp (singularity)
In the mathematical theory of singularities a cusp is a type of singular point of a curve. Cusps are local singularities in that they are not formed by self intersection points of the curve....
. A reducible plane cubic curve is either a conic and a line or three lines, and accordingly have two double points or a tacnode
Tacnode
In geometry, a tacnode is a kind of singular point of a curve. It is defined as a point where two osculating circles to the curve at that point are tangent. This means that two branches of the curve have ordinary tangency at the double point. The canonical example is = 0...
(if a conic and a line), or up to three double points or a single triple point (concurrent lines) if three lines.
Cubic curves in the plane of a triangle
Suppose that ABC is a triangle with sidelengths a = |BC|, b = |CA|, c = |AB|. Relative to ABC, many named cubics pass through well known points. Examples shown below use two kinds of homogeneous coordinates: trilinear and barycentric.To convert from trilinear to barycentric in a cubic equation, substitute as follows:
x → bcx, y → cay, z → abz;
to convert from barycentric to trilinear, use
x → ax, y → by, z → cz.
Many equations for cubics have the form
f(a,b,c,x,y,z) + f(b,c,a,y,z,x) + f(c,a,b,z,x,y) = 0.
In the examples below, such equations are written more succinctly in "cyclic sum notation", like this:
[cyclic sum f(x,y,z,a,b,c)] = 0.
The cubics listed below can be defined in terms of the isogonal conjugate, denoted by X*, of a point X not on a sideline of ABC. A construction of X* follows. Let LA be the reflection of line XA about the internal angle bisector of angle A, and define LB and LC analogously. Then the three reflected lines concur in X*. In trilinear coordinates, if X = x:y:z, then X* = 1/x:1/y:1/z.
Neuberg cubic
Trilinear equation: [cyclic sum (cos A - 2 cos B cos C)x(y2 - z2)] = 0Barycentric equation: [cyclic sum (a2(b2 - c2) - (b2 - c2 - 2a4)2)x(c2y2 - b2z2)] = 0
The Neuberg cubic (named after Joseph Jean Baptiste Neuberg
Joseph Jean Baptiste Neuberg
Joseph Jean Baptiste Neuberg was a Luxembourger mathematician who worked primarily in geometry.-Biography:Neuberg was born on 30 October 1840 in Luxembourg City, Luxembourg. He first studied at a local school, the Athénée de Luxembourg, then progressed to Ghent University, studying at the École...
) is the locus of a point X such that X* is on the line EX, where E is the Euler infinity point (X(30) in the Encyclopedia of Triangle Centers
Encyclopedia of Triangle Centers
The Encyclopedia of Triangle Centers is an on-line list of more than 3,000 points or "centers" associated with the geometry of a triangle. It is maintained by Clark Kimberling, Professor of Mathematics at the University of Evansville....
). Also, this cubic is the locus of X such that the triangle XAXBXC is perspective to ABC, where XAXBXC is the reflection of X in the lines BC, CA, AB, respectively
The Neuberg cubic passes through the following points: incenter, circumcenter, orthocenter, both Fermat points, both isodynamic points, the Euler infinity point, other triangle centers, the excenters, the reflections of A, B, C in the sidelines of ABC, and the vertices of the six equilateral triangles erected on the sides of ABC.
For a graphical representation and extensive list of properties of the Neuberg cubic, see K001 at Berhard Gibert's Cubics in the Triangle Plane.
Thomson cubic
Trilinear equation: [cyclic sum bcx(y2 - z2)] = 0Barycentric equation: [cyclic sum x(c2y2 - b2z2)] = 0
The Thomson cubic is the locus of a point X such that X* is on the line GX, where G is the centroid.
The Thomson cubic passes through the following points: incenter, centroid, circumcenter, orthocenter, symmedian point, other triangle centers, the vertices A, B, C, the excenters, the midpoints of sides BC, CA, AB, and the midpoints of the altitudes of ABC. For each point P on the cubic but not on a sideline of the cubic, the isogonal conjugate of P is also on the cubic.
For graphs and properties, see K002 at Cubics in the Triangle Plane.
Darboux cubic
Trilinear equation: [cyclic sum (cos A - cos B cos C)x(y2 - z2)] = 0Barycentric equation: [cyclic sum (2a2(b2 + c2) + (b2 - c2)2 - 3a4)x(c2y2 - b2z2)] = 0
The Darboux cubic is the locus of a point X such that X* is on the line LX, where L is the de Longchamps point, (L = X(20) in the Encyclopedia of Triangle Centers
Encyclopedia of Triangle Centers
The Encyclopedia of Triangle Centers is an on-line list of more than 3,000 points or "centers" associated with the geometry of a triangle. It is maintained by Clark Kimberling, Professor of Mathematics at the University of Evansville....
). Also, this cubic is the locus of X such that the pedal triangle of X is the cevian of some point (which lies on the Lucas cubic). Also, this cubic is the locus of a point X such that the pedal triangle of X and the anticevian triangle of X are perspective; the perspector lies on the Thomson cubic.
The Darboux cubic passes through the incenter, circumcenter, orthocenter, de Longchamps point, other triangle centers, the vertices A, B, C, the excenters, and the antipodes of A, B, C on the circumcircle. For each point P on the cubic but not on a sideline of the cubic, the isogonal conjugate of P is also on the cubic.
For graphics and properties, see K004 at Cubics in the Triangle Plane.
Napoleon-Feuerbach cubic
Trilinear equation: [cyclic sum cos(B - C)x(y2 - z2)] = 0Barycentric equation: [cyclic sum (a2(b2 - c2) - (b2 - c2)2)x(c2y2 - b2z2)] = 0
The Napoleon-Feuerbach cubic is the locus of a point X* is on the line NX, where N is the nine-point center, (N = X(5) in the Encyclopedia of Triangle Centers
Encyclopedia of Triangle Centers
The Encyclopedia of Triangle Centers is an on-line list of more than 3,000 points or "centers" associated with the geometry of a triangle. It is maintained by Clark Kimberling, Professor of Mathematics at the University of Evansville....
).
The Napoleon-Feuerbach cubic passes through the incenter, circumcenter, orthocenter, 1st and 2nd Napoleon points, other triangle centers, the vertices A, B, C, the excenters, the projections of the centroid on the altitudes, and the centers of the 6 equilateral triangles erected on the sides of ABC.
For a graphics and properties, see K005 at Cubics in the Triangle Plane.
Lucas cubic
Trilinear equation: [cyclic sum (cos A)x(b2y2 - c2z2)] = 0Barycentric equation: [cyclic sum (b2 + c2 - a2)x(y2 - z2)] = 0
The Lucas cubic is the locus of a point X such that the cevian triangle of X is the pedal triangle of some point; the point lies on the Darboux cubic.
The Lucas cubic passes through the centroid, orthocenter, Gergonne point, Nagel point, de Longchamps point, other triangle centers, the vertices of the anticomplementary triangle, and the foci of the Steiner circumellipse.
For graphics and properties, see K007 at Cubics in the Triangle Plane.
1st Brocard cubic
Trilinear equation: [cyclic sum bc(a4 - b2c2)x(y2 + z2] = 0Barycentric equation: [cyclic sum (a4 - b2c2)x(c2y2 + b2z2] = 0
Let A'B'C' be the 1st Brocard triangle. For arbitrary point X, let XA, XB, XC be the intersections of the lines XA' , XB' , XC' with the sidelines BC, CA, AB, respectively. The 1st Brocard cubic is the locus of X for which the points XA, XB, XC are collinear.
The 1st Brocard cubic passes through the centroid, symmedian point, Steiner point, other triangle centers, and the vertices of the 1st and 3rd Brocard triangles.
For graphics and properties, see K017 at Cubics in the Triangle Plane.
2nd Brocard cubic
Trilinear equation: [cyclic sum bc(b2 - c2)x(y2 + z2] = 0Barycentric equation: [cyclic sum (b2 - c2)x(c2y2 + b2z2] = 0
The 2nd Brocard cubic is the locus of a point X for which the pole of the line XX* in the circumconic through X and X* lies on the line of the circumcenter and the symmedian point (i.e., the Brocard axis).
The 2nd Brocard cubic passes through the centroid, symmedian point, both Fermat points, both isodynamic points, the Parry point, other triangle centers, and the vertices of the 2nd and 4th Brocard triangles.
For a graphics and properties, see K018 at Cubics in the Triangle Plane.
1st equal areas cubic
Trilinear equation: [cyclic sum a(b2 - c2)x(y2 - z2] = 0Barycentric equation: [cyclic sum a2(b2 - c2)x(c2y2 - b2z2] = 0
The 1st equal areas cubic is the locus of a point X such that area of the cevian triangle of X equals the area of the cevian triangle of X*. Also, this cubic is the locus of X for which X* is on the line S*X, where S is the Steiner point. (S = X(99) in the Encyclopedia of Triangle Centers
Encyclopedia of Triangle Centers
The Encyclopedia of Triangle Centers is an on-line list of more than 3,000 points or "centers" associated with the geometry of a triangle. It is maintained by Clark Kimberling, Professor of Mathematics at the University of Evansville....
).
The 1st equal areas cubic passes through the incenter, Steiner point, other triangle centers, the 1st and 2nd Brocard points, and the excenters.
For a graphics and properties, see K021 at Cubics in the Triangle Plane.
2nd equal areas cubic
Trilinear equation: (bz+cx)(cx+ay)(ay+bz) = (bx+cy)(cy+ax)(az+bx)Barycentric equation: [cyclic sum a(a2 - bc)x(c3y2 - b3z2)] = 0
For any point X = x:y:z (trilinears), let XY = y:z:x and XZ = z:x:y. The 2nd equal areas cubic is the locus of X such that the area of the cevian triangle of XY equals the area of the cevian triangle of XZ.
The 2nd equal areas cubic passes through the incenter, centroid, symmedian point, and points in Encyclopedia of Triangle Centers
Encyclopedia of Triangle Centers
The Encyclopedia of Triangle Centers is an on-line list of more than 3,000 points or "centers" associated with the geometry of a triangle. It is maintained by Clark Kimberling, Professor of Mathematics at the University of Evansville....
indexed as X(31), X(105), X(238), X(292), X(365), X(672), X(1453), X(1931), X(2053), and others.
For a graphics and properties, see K155 at Cubics in the Triangle Plane.
See also
- Cayley–Bacharach theorem, on the intersection of two cubic plane curves
- Twisted cubicTwisted cubicIn mathematics, a twisted cubic is a smooth, rational curve C of degree three in projective 3-space P3. It is a fundamental example of a skew curve. It is essentially unique, up to projective transformation...
, a cubic space curve - Elliptic curveElliptic curveIn mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...

