Normal surface
Encyclopedia
In mathematics
, a normal surface is a surface
inside a triangulated 3-manifold
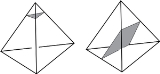
that intersects each tetrahedron so that each component of intersection is a triangle or a quad (see figure). A triangle cuts off a vertex of the tetrahedron while a quad separates pairs of vertices. A normal surface may have many components of intersection, called normal disks, with one tetrahedron, but no two normal disks can be quads that separate different pairs of vertices since that would lead to the surface self-intersecting.
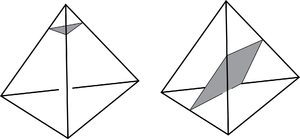Dually, a normal surface can be considered to be a surface that intersects each handle of a given handle structure on the 3-manifold in a prescribed manner similar to the above.
The concept of normal surface can be generalized to arbitrary polyhedra. There is also a related notion of almost normal surface.
The concept of normal surface is due to Hellmuth Kneser
, who utilized it in his proof of the prime decomposition theorem
for 3-manifolds. Later Wolfgang Haken
extended and refined the notion to create normal surface theory, which is at the basis of many of the algorithms in 3-manifold theory. The notion of almost normal surfaces is due to Hyam Rubinstein.
Regina
is software which enumerates normal and almost-normal surfaces in triangulated 3-manifolds, implementing Rubinstein's 3-sphere recognition algorithm, among other things.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a normal surface is a surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
inside a triangulated 3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
that intersects each tetrahedron so that each component of intersection is a triangle or a quad (see figure). A triangle cuts off a vertex of the tetrahedron while a quad separates pairs of vertices. A normal surface may have many components of intersection, called normal disks, with one tetrahedron, but no two normal disks can be quads that separate different pairs of vertices since that would lead to the surface self-intersecting.
The concept of normal surface can be generalized to arbitrary polyhedra. There is also a related notion of almost normal surface.
The concept of normal surface is due to Hellmuth Kneser
Hellmuth Kneser
Hellmuth Kneser was a German mathematician, who made notable contributions to group theory and topology. His most famous result may be his theorem on the existence of a prime decomposition for 3-manifolds...
, who utilized it in his proof of the prime decomposition theorem
Prime decomposition (3-manifold)
In mathematics, the prime decomposition theorem for 3-manifolds states that every compact, orientable 3-manifold is the connected sum of a unique collection of prime 3-manifolds....
for 3-manifolds. Later Wolfgang Haken
Wolfgang Haken
Wolfgang Haken is a mathematician who specializes in topology, in particular 3-manifolds.In 1976 together with colleague Kenneth Appel at the University of Illinois at Urbana-Champaign, Haken solved one of the most famous problems in mathematics, the four-color theorem...
extended and refined the notion to create normal surface theory, which is at the basis of many of the algorithms in 3-manifold theory. The notion of almost normal surfaces is due to Hyam Rubinstein.
Regina
Regina (program)
Regina is a suite of mathematical software for 3-manifold topologists. It focuses upon the study of 3-manifold triangulations and includes support for normal surfaces and angle structures.- Features :...
is software which enumerates normal and almost-normal surfaces in triangulated 3-manifolds, implementing Rubinstein's 3-sphere recognition algorithm, among other things.