Control volume
Encyclopedia
In fluid mechanics
and thermodynamics
, a control volume is a mathematical abstraction employed in the process of creating mathematical model
s of physical processes. In an inertial frame of reference
, it is a volume fixed in space or moving with constant velocity through which the fluid
(gas
or liquid
) flows. The surface enclosing the control volume is referred to as the control surface.
At steady state
, a control volume can be thought of as an arbitrary volume in which the mass of the fluid remains constant. As fluid moves through the control volume, the mass entering the control volume is equal to the mass leaving the control volume. At steady state
, and in the absence of work and heat transfer, the energy within the control volume remains constant. It is analogous to the classical mechanics concept of the Free body diagram
.
applies to the system under consideration, one first begins by considering how it applies to a small, control volume, or "representative volume". There is nothing special about a particular control volume, it simply represents a small part of the system to which physical laws can be easily applied. This gives rise to what is termed a volumetric, or volume-wise formulation of the mathematical model.
One can then argue that since the physical law
s behave in a certain way on a particular control volume, they behave the same way on all such volumes, since that particular control volume was not special in any way. In this way, the corresponding point-wise formulation of the mathematical model
can be developed so it can describe the physical behaviour of an entire (and maybe more complex) system.
In fluid mechanics
the conservation equations (for instance, the Navier-Stokes equations
) are in integral form. They therefore apply on volumes. Finding forms of the equation that are independent of the control volumes allows simplification of the integral signs.
often require that the regular time derivation
operator
is replaced by the substantive derivative operator
.
This can be seen as follows.
Consider a bug that is moving through a volume where there is some scalar
,
e.g. pressure
, that varies with time and position:
.
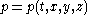If the bug during the time interval from
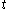
to
moves from
to
,
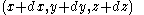then the bug experiences a change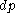
in the scalar value,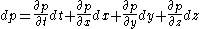
(the total differential
). If the bug is moving with velocity
,
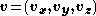the change in position is
,
and we may write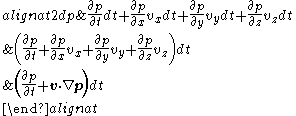
.
where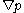
is the gradient
of the scalar field p. If the bug is just a fluid particle moving with the fluid's velocity field, the same formula applies, but now the velocity vector is that of the fluid.
The last parenthesized expression is the substantive derivative of the scalar pressure.
Since the pressure p in this computation is an arbitrary scalar field, we may abstract it and write the substantive derivative operator as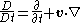
.
Fluid mechanics
Fluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...
and thermodynamics
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
, a control volume is a mathematical abstraction employed in the process of creating mathematical model
Mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
s of physical processes. In an inertial frame of reference
Inertial frame of reference
In physics, an inertial frame of reference is a frame of reference that describes time homogeneously and space homogeneously, isotropically, and in a time-independent manner.All inertial frames are in a state of constant, rectilinear motion with respect to one another; they are not...
, it is a volume fixed in space or moving with constant velocity through which the fluid
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
(gas
Gas
Gas is one of the three classical states of matter . Near absolute zero, a substance exists as a solid. As heat is added to this substance it melts into a liquid at its melting point , boils into a gas at its boiling point, and if heated high enough would enter a plasma state in which the electrons...
or liquid
Liquid
Liquid is one of the three classical states of matter . Like a gas, a liquid is able to flow and take the shape of a container. Some liquids resist compression, while others can be compressed. Unlike a gas, a liquid does not disperse to fill every space of a container, and maintains a fairly...
) flows. The surface enclosing the control volume is referred to as the control surface.
At steady state
Steady state
A system in a steady state has numerous properties that are unchanging in time. This implies that for any property p of the system, the partial derivative with respect to time is zero:...
, a control volume can be thought of as an arbitrary volume in which the mass of the fluid remains constant. As fluid moves through the control volume, the mass entering the control volume is equal to the mass leaving the control volume. At steady state
Steady state
A system in a steady state has numerous properties that are unchanging in time. This implies that for any property p of the system, the partial derivative with respect to time is zero:...
, and in the absence of work and heat transfer, the energy within the control volume remains constant. It is analogous to the classical mechanics concept of the Free body diagram
Free body diagram
A free body diagram, also called a force diagram, is a pictorial representation often used by physicists and engineers to analyze the forces acting on a body of interest. A free body diagram shows all forces of all types acting on this body. Drawing such a diagram can aid in solving for the unknown...
.
Overview
Typically, to understand how a given physical lawPhysical law
A physical law or scientific law is "a theoretical principle deduced from particular facts, applicable to a defined group or class of phenomena, and expressible by the statement that a particular phenomenon always occurs if certain conditions be present." Physical laws are typically conclusions...
applies to the system under consideration, one first begins by considering how it applies to a small, control volume, or "representative volume". There is nothing special about a particular control volume, it simply represents a small part of the system to which physical laws can be easily applied. This gives rise to what is termed a volumetric, or volume-wise formulation of the mathematical model.
One can then argue that since the physical law
Physical law
A physical law or scientific law is "a theoretical principle deduced from particular facts, applicable to a defined group or class of phenomena, and expressible by the statement that a particular phenomenon always occurs if certain conditions be present." Physical laws are typically conclusions...
s behave in a certain way on a particular control volume, they behave the same way on all such volumes, since that particular control volume was not special in any way. In this way, the corresponding point-wise formulation of the mathematical model
Mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
can be developed so it can describe the physical behaviour of an entire (and maybe more complex) system.
In fluid mechanics
Fluid mechanics
Fluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...
the conservation equations (for instance, the Navier-Stokes equations
Navier-Stokes equations
In physics, the Navier–Stokes equations, named after Claude-Louis Navier and George Gabriel Stokes, describe the motion of fluid substances. These equations arise from applying Newton's second law to fluid motion, together with the assumption that the fluid stress is the sum of a diffusing viscous...
) are in integral form. They therefore apply on volumes. Finding forms of the equation that are independent of the control volumes allows simplification of the integral signs.
Substantive derivative
Computations in fluid mechanicsFluid mechanics
Fluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...
often require that the regular time derivation
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
operator
is replaced by the substantive derivative operator
.This can be seen as follows.
Consider a bug that is moving through a volume where there is some scalar
Scalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
,
e.g. pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
, that varies with time and position:
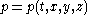.If the bug during the time interval from
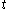
to
moves from
to
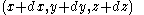,then the bug experiences a change
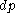in the scalar value,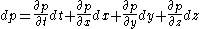(the total differential
Total derivative
In the mathematical field of differential calculus, the term total derivative has a number of closely related meanings.The total derivative of a function f, of several variables, e.g., t, x, y, etc., with respect to one of its input variables, e.g., t, is different from the partial derivative...
). If the bug is moving with velocity
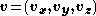,the change in position is
,and we may write
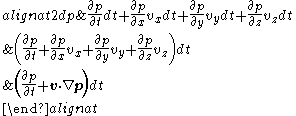.where
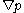is the gradientGradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of the scalar field p. If the bug is just a fluid particle moving with the fluid's velocity field, the same formula applies, but now the velocity vector is that of the fluid.
The last parenthesized expression is the substantive derivative of the scalar pressure.
Since the pressure p in this computation is an arbitrary scalar field, we may abstract it and write the substantive derivative operator as
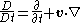.See also
- Navier-Stokes equationsNavier-Stokes equationsIn physics, the Navier–Stokes equations, named after Claude-Louis Navier and George Gabriel Stokes, describe the motion of fluid substances. These equations arise from applying Newton's second law to fluid motion, together with the assumption that the fluid stress is the sum of a diffusing viscous...
- Special RelativitySpecial relativitySpecial relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
- Substantive Derivative
- Fluid MechanicsFluid mechanicsFluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...