Continuous-time Markov process
Encyclopedia
In probability theory
, a continuous-time Markov process
is a stochastic process
{ X(t) : t ≥ 0 } that satisfies the Markov property
and takes values from a set called the state space
; it is the continuous-time version of a Markov chain
. The Markov property states that at any times s > t > 0, the conditional probability distribution
of the process at time s given the whole history of the process up to and including time t, depends only on the state of the process at time t. In effect, the state of the process at time s is conditionally independent
of the history of the process before time t, given the state of the process at time t.
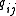between states i and j. Let X(t) be the random variable describing the state of the process at time t, and assume that the process is in a state i at time t. 
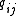(for 
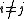) measures how quickly that 
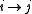transition happens. Precisely, after a tiny amount of time h, the probability the state is now j is given by
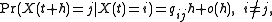
where o(h) represents a quantity that goes to zero faster than h goes to zero (see the article on order notation). Hence, over a sufficiently small interval of time, the probability of a particular transition (between different states) is roughly proportional to the duration of that interval. The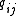
are called transition rates because if we have a large ensemble of n systems in state i, they will switch over to state j at an average rate of 
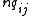until n decreases appreciably.
The transition rates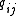
are typically given as the ij-th elements of the transition rate matrix Q (also known as an intensity matrix). As the transition rate matrix contains rates, the rate of departing from one state to arrive at another should be positive, and the rate that the system remains in a state should be negative. The rates for a given state should sum to zero, yielding the diagonal elements to be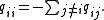
With this notation, and letting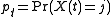
, the evolution of a continuous-time Markov process is given by the first-order differential equation
The probability that no transition happens in some time r is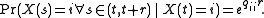
That is, the probability distribution
of the waiting time until the first transition is an exponential distribution
with rate parameter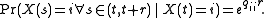
, and continuous-time Markov processes are thus memoryless
processes.
A time dependent (time heterogeneous) Markov process is a Markov process as above, but with the q-rate a function of time, denoted qij(t).
of transitioning from state i into state j. These conditional probabilities may be found by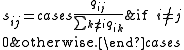
From this, S may be written as
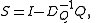
where DQ = diag{Q} is the diagonal matrix
of Q.
To find the stationary probability distribution vector, we must next find φ such that
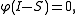
with φ being a row vector, such that all elements in φ are greater than 0 and
= 1, and the 0 on the right side also being a row vector of 0's. From this, π may be found as
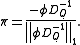
Note that S may be periodic, even if Q is not. Once π is found, it must be normalized to a unit vector.
Another discrete-time process that may be derived from a continuous-time Markov chain is a δ-skeleton—the (discrete-time) Markov chain formed by observing X(t) at intervals of δ units of time. The random variables X(0), X(δ), X(2δ), ... give the sequence of states visited by the δ-skeleton.
and a Poisson arrival
rate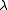
. Then the number of jobs in the queue is a continuous time markov process on the non-negative integers. The transition rate from one number to the next (meaning a new job arrives within the next instant) is 
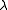, and the transition rate to the next lowest number (meaning a job completes in the next instant) is 
.
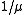Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, a continuous-time Markov process
Markov process
In probability theory and statistics, a Markov process, named after the Russian mathematician Andrey Markov, is a time-varying random phenomenon for which a specific property holds...
is a stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
{ X(t) : t ≥ 0 } that satisfies the Markov property
Markov property
In probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process. It was named after the Russian mathematician Andrey Markov....
and takes values from a set called the state space
State space
In the theory of discrete dynamical systems, a state space is a directed graph where each possible state of a dynamical system is represented by a vertex, and there is a directed edge from a to b if and only if ƒ = b where the function f defines the dynamical system.State spaces are...
; it is the continuous-time version of a Markov chain
Markov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
. The Markov property states that at any times s > t > 0, the conditional probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of the process at time s given the whole history of the process up to and including time t, depends only on the state of the process at time t. In effect, the state of the process at time s is conditionally independent
Conditional independence
In probability theory, two events R and B are conditionally independent given a third event Y precisely if the occurrence or non-occurrence of R and the occurrence or non-occurrence of B are independent events in their conditional probability distribution given Y...
of the history of the process before time t, given the state of the process at time t.
Mathematical definitions
A Markov process, like a Markov chain, can be thought of as a directed graph of states of the system. The difference is that, rather than transitioning to a new (possibly the same) state at each time step, the system will remain in the current state for some random (in particular, exponentially distributed) amount of time and then transition to a different state. The process is characterized by "transition rates"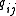 between states i and j. Let X(t) be the random variable describing the state of the process at time t, and assume that the process is in a state i at time t. 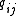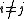(for ) measures how quickly that 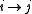transition happens. Precisely, after a tiny amount of time h, the probability the state is now j is given by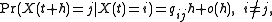 where o(h) represents a quantity that goes to zero faster than h goes to zero (see the article on order notation). Hence, over a sufficiently small interval of time, the probability of a particular transition (between different states) is roughly proportional to the duration of that interval. The
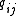are called transition rates because if we have a large ensemble of n systems in state i, they will switch over to state j at an average rate of 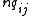until n decreases appreciably.The transition rates
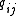are typically given as the ij-th elements of the transition rate matrix Q (also known as an intensity matrix). As the transition rate matrix contains rates, the rate of departing from one state to arrive at another should be positive, and the rate that the system remains in a state should be negative. The rates for a given state should sum to zero, yielding the diagonal elements to be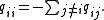With this notation, and letting
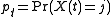, the evolution of a continuous-time Markov process is given by the first-order differential equation
The probability that no transition happens in some time r is
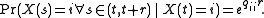
That is, the probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of the waiting time until the first transition is an exponential distribution
Exponential distribution
In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
with rate parameter
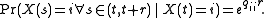, and continuous-time Markov processes are thus memorylessMemorylessness
In probability and statistics, memorylessness is a property of certain probability distributions: the exponential distributions of non-negative real numbers and the geometric distributions of non-negative integers....
processes.
A time dependent (time heterogeneous) Markov process is a Markov process as above, but with the q-rate a function of time, denoted qij(t).
Embedded Markov chain
One method of finding the stationary probability distribution, π, of an ergodic continuous-time Markov process, Q, is by first finding its embedded Markov chain (EMC). Strictly speaking, the EMC is a regular discrete-time Markov chain, sometimes referred to as a jump process. Each element of the one-step transition probability matrix of the EMC, S, is denoted by sij, and represents the conditional probabilityConditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
of transitioning from state i into state j. These conditional probabilities may be found by
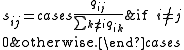
From this, S may be written as
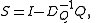
where DQ = diag{Q} is the diagonal matrix
Diagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
of Q.
To find the stationary probability distribution vector, we must next find φ such that
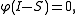
with φ being a row vector, such that all elements in φ are greater than 0 and
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
= 1, and the 0 on the right side also being a row vector of 0's. From this, π may be found as
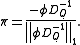
Note that S may be periodic, even if Q is not. Once π is found, it must be normalized to a unit vector.
Another discrete-time process that may be derived from a continuous-time Markov chain is a δ-skeleton—the (discrete-time) Markov chain formed by observing X(t) at intervals of δ units of time. The random variables X(0), X(δ), X(2δ), ... give the sequence of states visited by the δ-skeleton.
Applications
Markov processes are used to describe physical processes where a system evolves in constant time. Sometimes, rather than a single systems, they are applied to an ensemble of identical, independent systems, and the probabilities are used to find how many members of the ensemble are in a given state.Chemical reactions
Imagine a large number n of molecules in solution in state A, each of which can undergo a chemical reaction to state B with a certain average rate. Perhaps the molecule is an enzyme, and the states refer to how it is folded. The state of any single enzyme follows a Markov process, and since the molecules are essentially independent of each other, the number of molecules in state A or B at a time is n times the probability a given molecule is in that state.Queueing theory
As a simple example, imagine a first-come-first-served queue where the jobs have exponential size distribution with average size and a Poisson arrivalPoisson process
A Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...
rate
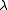. Then the number of jobs in the queue is a continuous time markov process on the non-negative integers. The transition rate from one number to the next (meaning a new job arrives within the next instant) is 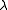, and the transition rate to the next lowest number (meaning a job completes in the next instant) is 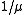.See also
- Markov chainMarkov chainA Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
- Master equationMaster equationIn physics and chemistry and related fields, master equations are used to describe the time-evolution of a system that can be modelled as being in exactly one of countable number of states at any given time, and where switching between states is treated probabilistically...
(physics) - Queueing theoryQueueing theoryQueueing theory is the mathematical study of waiting lines, or queues. The theory enables mathematical analysis of several related processes, including arriving at the queue, waiting in the queue , and being served at the front of the queue...
- Phase-type distributionPhase-type distributionA phase-type distribution is a probability distribution that results from a system of one or more inter-related Poisson processes occurring in sequence, or phases. The sequence in which each of the phases occur may itself be a stochastic process. The distribution can be represented by a random...
- Semi-Markov processSemi-Markov processA continuous-time stochastic process is called a semi-Markov process or 'Markov renewal process' if the embedded jump chain is a Markov chain, and where the holding times are random variables with any distribution, whose distribution function may depend on the two states between which the move is...
- Variable-order Markov modelVariable-order Markov modelVariable-order Markov models are an important class of models that extend the well known Markov chain models. In contrast to the Markov chain models, where each random variable in a sequence with a Markov property depends on a fixed number of random variables, in VOM models this number of...