
Variable-order Markov model
Encyclopedia
Variable-order Markov models are an important class of models that extend the well known Markov chain
models. In contrast to the Markov chain models, where each random variable in a sequence with a Markov property
depends on a fixed number of random variable
s, in VOM models this number of conditioning random variables may vary based on the specific observed realization.
This realization sequence is often called the context; therefore the VOM models are also called context trees . The flexibility in the number of conditioning random variable
s turns out to be of real advantage for many applications, such as statistical analysis, classification and prediction.
s, each of which takes a value from the ternary alphabet
{a, b, c}. Specifically, consider the string aaabcaaabcaaabcaaabc...aaabc constructed from infinite concatenations of the sub-string aaabc.
The VOM model of maximal order 2 can approximate the above string using only the following five conditional probability
components: {Pr(a|aa) = 0.5, Pr(b|aa) = 0.5, Pr(c|b) = 1.0, Pr(a|c)= 1.0, Pr(a|ca)= 1.0}.
In this example, Pr(c|ab) = Pr(c|b) = 1.0; therefore, the shorter context b is sufficient to determine the next character. Similarly, the VOM model of maximal order 3 can generate the string exactly using only five conditional probability components, which are all equal to 1.0.
To construct the Markov chain
of order 1 for the next character in that string, one must estimate the following 9 conditional probability components: {Pr(a|a), Pr(a|b), Pr(a|c), Pr(b|a), Pr(b|b), Pr(b|c), Pr(c|a), Pr(c|b), Pr(c|c)}. To construct the Markov chain of order 2 for the next character, one must estimate 27 conditional probability components: {Pr(a|aa), Pr(a|ab), ..., Pr(c|cc)}. And to construct the Markov chain of order three for the next character one must estimate the following 81 conditional probability components: {Pr(a|aaa), Pr(a|aab), ..., Pr(c|ccc)}.
In practical settings there is seldom sufficient data to accurately estimate the exponentially increasing
number of conditional probability components as the order of the Markov chain increases.
The variable-order Markov model assumes that in realistic settings, there are certain realizations of states (represented by contexts) in which some past states are independent from the future states; accordingly, "a great reduction in the number of model parameters can be achieved."
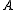 be a state space (finite alphabet
be a state space (finite alphabet
) of size|A| .
Consider a sequence with the Markov property
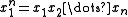 of
of  realizations of random variable
realizations of random variable
s, where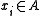 is the state (symbol) at position
is the state (symbol) at position 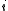 1≤
1≤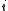 ≤
≤ , and the concatenation of states
, and the concatenation of states 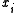 and
and 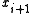 is denoted by
is denoted by 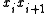 .
.
Given a training set of observed states,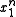 , the construction algorithm of the VOM models learns a model
, the construction algorithm of the VOM models learns a model 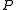 that provides a probability
that provides a probability
assignment for each state in the sequence given its past (previously observed symbols) or future states.
Specifically, the learner generates a conditional probability distribution
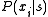 for a symbol
for a symbol 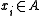 given a context
given a context 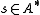 , where the * sign represents a sequence of states of any length, including the empty context.
, where the * sign represents a sequence of states of any length, including the empty context.
VOM models attempt to estimate conditional distribution
s of the form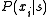 where the context length |
where the context length | |≤
|≤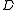 varies depending on the available statistics.
varies depending on the available statistics.
In contrast, conventional Markov models
attempt to estimate these conditional distribution
s by assuming a fixed contexts' length | |=
|=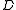 and, hence, can be considered as special cases of the VOM models.
and, hence, can be considered as special cases of the VOM models.
Effectively, for a given training sequence, the VOM models are found to obtain better model parameterization than the fixed-order Markov models
that leads to a better variance
-bias tradeoff of the learned models.
VOM models have been successfully applied to areas such as machine learning
, information theory
and bioinformatics
, including specific applications such as coding
and data compression
, document compression, classification and identification of DNA
and protein sequences
, statistical process control
, spam filtering and others.
Markov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
models. In contrast to the Markov chain models, where each random variable in a sequence with a Markov property
Markov property
In probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process. It was named after the Russian mathematician Andrey Markov....
depends on a fixed number of random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s, in VOM models this number of conditioning random variables may vary based on the specific observed realization.
This realization sequence is often called the context; therefore the VOM models are also called context trees . The flexibility in the number of conditioning random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s turns out to be of real advantage for many applications, such as statistical analysis, classification and prediction.
Example
Consider for example a sequence of random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s, each of which takes a value from the ternary alphabet
Alphabet
An alphabet is a standard set of letters—basic written symbols or graphemes—each of which represents a phoneme in a spoken language, either as it exists now or as it was in the past. There are other systems, such as logographies, in which each character represents a word, morpheme, or semantic...
{a, b, c}. Specifically, consider the string aaabcaaabcaaabcaaabc...aaabc constructed from infinite concatenations of the sub-string aaabc.
The VOM model of maximal order 2 can approximate the above string using only the following five conditional probability
Conditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
components: {Pr(a|aa) = 0.5, Pr(b|aa) = 0.5, Pr(c|b) = 1.0, Pr(a|c)= 1.0, Pr(a|ca)= 1.0}.
In this example, Pr(c|ab) = Pr(c|b) = 1.0; therefore, the shorter context b is sufficient to determine the next character. Similarly, the VOM model of maximal order 3 can generate the string exactly using only five conditional probability components, which are all equal to 1.0.
To construct the Markov chain
Markov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
of order 1 for the next character in that string, one must estimate the following 9 conditional probability components: {Pr(a|a), Pr(a|b), Pr(a|c), Pr(b|a), Pr(b|b), Pr(b|c), Pr(c|a), Pr(c|b), Pr(c|c)}. To construct the Markov chain of order 2 for the next character, one must estimate 27 conditional probability components: {Pr(a|aa), Pr(a|ab), ..., Pr(c|cc)}. And to construct the Markov chain of order three for the next character one must estimate the following 81 conditional probability components: {Pr(a|aaa), Pr(a|aab), ..., Pr(c|ccc)}.
In practical settings there is seldom sufficient data to accurately estimate the exponentially increasing
Exponential growth
Exponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...
number of conditional probability components as the order of the Markov chain increases.
The variable-order Markov model assumes that in realistic settings, there are certain realizations of states (represented by contexts) in which some past states are independent from the future states; accordingly, "a great reduction in the number of model parameters can be achieved."
Definition
Let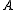 be a state space (finite alphabet
be a state space (finite alphabetAlphabet
An alphabet is a standard set of letters—basic written symbols or graphemes—each of which represents a phoneme in a spoken language, either as it exists now or as it was in the past. There are other systems, such as logographies, in which each character represents a word, morpheme, or semantic...
) of size
Consider a sequence with the Markov property
Markov property
In probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process. It was named after the Russian mathematician Andrey Markov....
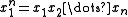 of
of  realizations of random variable
realizations of random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s, where
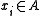 is the state (symbol) at position
is the state (symbol) at position 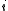 1≤
1≤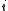 ≤
≤ , and the concatenation of states
, and the concatenation of states 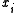 and
and 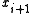 is denoted by
is denoted by 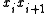 .
.Given a training set of observed states,
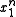 , the construction algorithm of the VOM models learns a model
, the construction algorithm of the VOM models learns a model 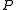 that provides a probability
that provides a probabilityProbability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
assignment for each state in the sequence given its past (previously observed symbols) or future states.
Specifically, the learner generates a conditional probability distribution
Conditional distribution
Given two jointly distributed random variables X and Y, the conditional probability distribution of Y given X is the probability distribution of Y when X is known to be a particular value...
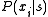 for a symbol
for a symbol 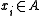 given a context
given a context 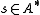 , where the * sign represents a sequence of states of any length, including the empty context.
, where the * sign represents a sequence of states of any length, including the empty context.VOM models attempt to estimate conditional distribution
Conditional distribution
Given two jointly distributed random variables X and Y, the conditional probability distribution of Y given X is the probability distribution of Y when X is known to be a particular value...
s of the form
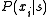 where the context length |
where the context length | |≤
|≤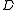 varies depending on the available statistics.
varies depending on the available statistics.In contrast, conventional Markov models
Markov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
attempt to estimate these conditional distribution
Conditional distribution
Given two jointly distributed random variables X and Y, the conditional probability distribution of Y given X is the probability distribution of Y when X is known to be a particular value...
s by assuming a fixed contexts' length |
 |=
|=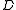 and, hence, can be considered as special cases of the VOM models.
and, hence, can be considered as special cases of the VOM models.Effectively, for a given training sequence, the VOM models are found to obtain better model parameterization than the fixed-order Markov models
Markov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
that leads to a better variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
-bias tradeoff of the learned models.
Application areas
Various efficient algorithms have been devised for estimating the parameters of the VOM model.VOM models have been successfully applied to areas such as machine learning
Machine learning
Machine learning, a branch of artificial intelligence, is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data, such as from sensor data or databases...
, information theory
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
and bioinformatics
Bioinformatics
Bioinformatics is the application of computer science and information technology to the field of biology and medicine. Bioinformatics deals with algorithms, databases and information systems, web technologies, artificial intelligence and soft computing, information and computation theory, software...
, including specific applications such as coding
Code
A code is a rule for converting a piece of information into another form or representation , not necessarily of the same type....
and data compression
Data compression
In computer science and information theory, data compression, source coding or bit-rate reduction is the process of encoding information using fewer bits than the original representation would use....
, document compression, classification and identification of DNA
DNA
Deoxyribonucleic acid is a nucleic acid that contains the genetic instructions used in the development and functioning of all known living organisms . The DNA segments that carry this genetic information are called genes, but other DNA sequences have structural purposes, or are involved in...
and protein sequences
Protein
Proteins are biochemical compounds consisting of one or more polypeptides typically folded into a globular or fibrous form, facilitating a biological function. A polypeptide is a single linear polymer chain of amino acids bonded together by peptide bonds between the carboxyl and amino groups of...
, statistical process control
Statistical process control
Statistical process control is the application of statistical methods to the monitoring and control of a process to ensure that it operates at its full potential to produce conforming product. Under SPC, a process behaves predictably to produce as much conforming product as possible with the least...
, spam filtering and others.
See also
- Markov chainMarkov chainA Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
- Examples of Markov chainsExamples of Markov chains- Board games played with dice :A game of snakes and ladders or any other game whose moves are determined entirely by dice is a Markov chain, indeed, an absorbing Markov chain. This is in contrast to card games such as blackjack, where the cards represent a 'memory' of the past moves. To see the...
- Variable order Bayesian network
- Markov processMarkov processIn probability theory and statistics, a Markov process, named after the Russian mathematician Andrey Markov, is a time-varying random phenomenon for which a specific property holds...
- Markov chain Monte CarloMarkov chain Monte CarloMarkov chain Monte Carlo methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. The state of the chain after a large number of steps is then used as a sample of the...
- Semi-Markov processSemi-Markov processA continuous-time stochastic process is called a semi-Markov process or 'Markov renewal process' if the embedded jump chain is a Markov chain, and where the holding times are random variables with any distribution, whose distribution function may depend on the two states between which the move is...
- BioinformaticsBioinformaticsBioinformatics is the application of computer science and information technology to the field of biology and medicine. Bioinformatics deals with algorithms, databases and information systems, web technologies, artificial intelligence and soft computing, information and computation theory, software...
- Machine learningMachine learningMachine learning, a branch of artificial intelligence, is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data, such as from sensor data or databases...
- Artificial intelligenceArtificial intelligenceArtificial intelligence is the intelligence of machines and the branch of computer science that aims to create it. AI textbooks define the field as "the study and design of intelligent agents" where an intelligent agent is a system that perceives its environment and takes actions that maximize its...

