
Conductor (class field theory)
Encyclopedia
In algebraic number theory
, the conductor of a finite abelian extension
of local
or global field
s provides a quantitative measure of the ramification
in the extension. The definition of the conductor is related to the Artin map.
 , is the smallest non-negative integer
, is the smallest non-negative integer
n such that the higher unit group is contained in NL/K(L×), where NL/K is field norm
is contained in NL/K(L×), where NL/K is field norm
map. Equivalently, n is smallest such that the local Artin map is trivial on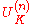 . Sometimes, the conductor is defined as
. Sometimes, the conductor is defined as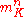
where n is as above and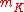 is the maximal ideal
is the maximal ideal
of K.
The conductor of an extension measures the ramification
. Qualitatively, the extension is unramified if, and only if, the conductor is zero, and it is tamely ramified if, and only if, the conductor is 1. More precisely, the conductor computes the non-triviality of higher ramification groups: if s is the largest integer for which the "lower-numbering" higher ramification group Gs is non-trivial, then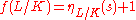 , where ηL/K is the function that translates from "lower-numbering" to "upper-numbering" of higher ramification groups.
, where ηL/K is the function that translates from "lower-numbering" to "upper-numbering" of higher ramification groups.
The conductor of L/K is also related to the Artin conductors of characters of the Galois group
Gal(L/K). Specifically,
where χ varies over all multiplicative complex characters of Gal(L/K),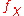 is the Artin conductor of χ, and lcm is the least common multiple
is the Artin conductor of χ, and lcm is the least common multiple
.

Additionally, the conductor can be defined when L and K are allowed to be slightly more general than local, namely if they are complete valued fields with quasi-finite
residue field.
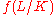 , is the smallest modulus
, is the smallest modulus
such that θ factors through the ray class group modulo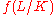 . It can also be defined as the greatest common divisor
. It can also be defined as the greatest common divisor
of all defining moduli of θ.
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
, the conductor of a finite abelian extension
Abelian extension
In abstract algebra, an abelian extension is a Galois extension whose Galois group is abelian. When the Galois group is a cyclic group, we have a cyclic extension. More generally, a Galois extension is called solvable if its Galois group is solvable....
of local
Local field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
or global field
Global field
In mathematics, the term global field refers to either of the following:*an algebraic number field, i.e., a finite extension of Q, or*a global function field, i.e., the function field of an algebraic curve over a finite field, equivalently, a finite extension of Fq, the field of rational functions...
s provides a quantitative measure of the ramification
Ramification
In mathematics, ramification is a geometric term used for 'branching out', in the way that the square root function, for complex numbers, can be seen to have two branches differing in sign...
in the extension. The definition of the conductor is related to the Artin map.
Local conductor
Let L/K be a finite abelian extension of non-archimedean local fields. The conductor of L/K, denoted , is the smallest non-negative integer
, is the smallest non-negative integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
n such that the higher unit group
 is contained in NL/K(L×), where NL/K is field norm
is contained in NL/K(L×), where NL/K is field normField norm
In mathematics, the norm is a mapping defined in field theory, to map elements of a larger field into a smaller one.-Formal definitions:1. Let K be a field and L a finite extension of K...
map. Equivalently, n is smallest such that the local Artin map is trivial on
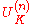 . Sometimes, the conductor is defined as
. Sometimes, the conductor is defined as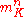
where n is as above and
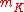 is the maximal ideal
is the maximal idealLocal field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
of K.
The conductor of an extension measures the ramification
Ramification
In mathematics, ramification is a geometric term used for 'branching out', in the way that the square root function, for complex numbers, can be seen to have two branches differing in sign...
. Qualitatively, the extension is unramified if, and only if, the conductor is zero, and it is tamely ramified if, and only if, the conductor is 1. More precisely, the conductor computes the non-triviality of higher ramification groups: if s is the largest integer for which the "lower-numbering" higher ramification group Gs is non-trivial, then
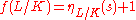 , where ηL/K is the function that translates from "lower-numbering" to "upper-numbering" of higher ramification groups.
, where ηL/K is the function that translates from "lower-numbering" to "upper-numbering" of higher ramification groups.The conductor of L/K is also related to the Artin conductors of characters of the Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
Gal(L/K). Specifically,

where χ varies over all multiplicative complex characters of Gal(L/K),
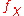 is the Artin conductor of χ, and lcm is the least common multiple
is the Artin conductor of χ, and lcm is the least common multipleLeast common multiple
In arithmetic and number theory, the least common multiple of two integers a and b, usually denoted by LCM, is the smallest positive integer that is a multiple of both a and b...
.
More general fields
The conductor can be defined in the same way for L/K a not necessarily abelian finite Galois extension of local fields. However, it only depends on Lab/K, the maximal abelian extension of K in L, because of the "norm limitation theorem", which states that, in this situation,
Additionally, the conductor can be defined when L and K are allowed to be slightly more general than local, namely if they are complete valued fields with quasi-finite
Quasi-finite field
In mathematics, a quasi-finite field is a generalisation of a finite field. Standard local class field theory usually deals with complete valued fields whose residue field is finite In mathematics, a quasi-finite field is a generalisation of a finite field. Standard local class field theory usually...
residue field.
Archimedean fields
Mostly for the sake of global conductors, the conductor of the trivial extension R/R is defined to be 0, and the conductor of the extension C/R is defined to be 1.Algebraic number fields
The conductor of an abelian extension L/K of number fields can be defined, similarly to the local case, using the Artin map. Specifically, let θ : Im → Gal(L/K) be the global Artin map where m is a defining modulus for L/K, then the conductor of L/K, denoted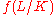 , is the smallest modulus
, is the smallest modulusModulus (algebraic number theory)
In mathematics, in the field of algebraic number theory, a modulus is a formal product of places of a global field...
such that θ factors through the ray class group modulo
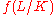 . It can also be defined as the greatest common divisor
. It can also be defined as the greatest common divisorGreatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
of all defining moduli of θ.
Example
- Let p be a prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
and let L/K be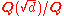 where d is a squarefree integer. Then,
where d is a squarefree integer. Then,
-

- where
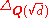 is the discriminantDiscriminant of an algebraic number fieldIn mathematics, the discriminant of an algebraic number field is a numerical invariant that, loosely speaking, measures the size of the algebraic number field...
is the discriminantDiscriminant of an algebraic number fieldIn mathematics, the discriminant of an algebraic number field is a numerical invariant that, loosely speaking, measures the size of the algebraic number field...
of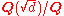 .
.
Relation to local conductors and ramification
The global conductor is the product of local conductors: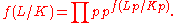
As a consequence, a finite prime is ramified in L/K if, and only if, it divides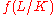 . An infinite prime v occurs in the conductor if, and only if, v is real and becomes complex in L.
. An infinite prime v occurs in the conductor if, and only if, v is real and becomes complex in L.
- where

