
Compound of six pentagonal antiprisms
Encyclopedia
| Compound of six pentagonal antiprisms | |
|---|---|
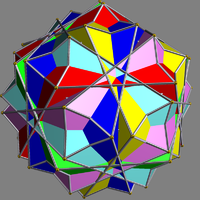 |
|
| Type | Uniform compound Uniform polyhedron compound A uniform polyhedron compound is a polyhedral compound whose constituents are identical uniform polyhedra, in an arrangement that is also uniform: the symmetry group of the compound acts transitively on the compound's vertices.The uniform polyhedron compounds were first enumerated by John Skilling... |
| Index | UC27 |
| Polyhedra | 6 pentagonal antiprism Pentagonal antiprism In geometry, the pentagonal antiprism is the third in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It consists of two pentagons joined to each other by a ring of 10 triangles for a total of 12 faces... s |
| Faces | 60 triangle Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... s, 12 pentagon Pentagon In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and... s |
| Edges | 120 |
| Vertices | 60 |
| Symmetry group Symmetry group The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation... |
icosahedral Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation... (Ih) |
| Subgroup Subgroup In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H... restricting to one constituent |
5-fold antiprismatic Dihedral symmetry in three dimensions This article deals with three infinite sequences of point groups in three dimensions which have a symmetry group that as abstract group is a dihedral group Dihn .See also point groups in two dimensions.Chiral:... (D5d) |
This uniform polyhedron compound
Uniform polyhedron compound
A uniform polyhedron compound is a polyhedral compound whose constituents are identical uniform polyhedra, in an arrangement that is also uniform: the symmetry group of the compound acts transitively on the compound's vertices.The uniform polyhedron compounds were first enumerated by John Skilling...
is a symmetric arrangement of 6 pentagonal antiprism
Pentagonal antiprism
In geometry, the pentagonal antiprism is the third in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It consists of two pentagons joined to each other by a ring of 10 triangles for a total of 12 faces...
s. It can be constructed by inscribing within an icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
one pentagonal antiprism in each of the six possible ways, and then rotating each by 36 degrees about its axis (that passes through the centres of the two opposite pentagonal faces).
It shares its vertex arrangement
Vertex arrangement
In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes....
with the compound of 6 pentagrammic crossed antiprisms
Compound of six pentagrammic crossed antiprisms
This uniform polyhedron compound is a symmetric arrangement of 6 pentagrammic crossed antiprisms. It can be constructed by inscribing within a great icosahedron one pentagrammic crossed antiprism in each of the six possible ways, and then rotating each by 36 degrees about its axis...
.
Cartesian coordinates
Cartesian coordinates for the vertices of this compound are all the cyclic permutations of- (±(3+4τ), 0, ±(4−3τ))
- (±(2−4τ), ±5τ, ±(1−2τ))
- (±(2+τ), ±5, ±(4+2τ))
where τ = (1+√5)/2 is the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
(sometimes written φ).

