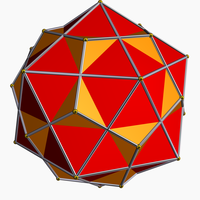
Compound of dodecahedron and icosahedron
Encyclopedia
| First stellation of icosidodecahedron | |
|---|---|
  |
|
| Type | Dual compound Polyhedral compound A polyhedral compound is a polyhedron that is itself composed of several other polyhedra sharing a common centre. They are the three-dimensional analogs of polygonal compounds such as the hexagram.... |
| Stellation Stellation Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again... core |
icosidodecahedron |
| Convex hull Convex hull In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X.... |
Rhombic triacontahedron Rhombic triacontahedron In geometry, the rhombic triacontahedron is a convex polyhedron with 30 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. It is the polyhedral dual of the icosidodecahedron, and it is a zonohedron.... |
| Index | W47 |
| Polyhedra | 1 icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids.... 1 dodecahedron |
| Faces | 20 triangle Triangle A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted .... s 12 pentagon Pentagon In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and... s |
| Edges | 60 |
| Vertices | 32 |
| Symmetry group Symmetry group The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation... |
icosahedral Icosahedral symmetry A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation... (Ih) |
In geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, this polyhedron can be seen as either a polyhedral stellation
Stellation
Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...
or a compound.
As a compound
It can be seen as the compound of an icosahedronIcosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
and dodecahedron. It is one of four compounds constructed from a Platonic solid
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
or Kepler-Poinsot solid
Kepler-Poinsot solid
In geometry, a Kepler–Poinsot polyhedron is any of four regular star polyhedra. They may be obtained by stellating the regular convex dodecahedron and icosahedron, and differ from these in having regular pentagrammic faces or vertex figures....
, and its dual.
It has icosahedral symmetry
Icosahedral symmetry
A regular icosahedron has 60 rotational symmetries, and a symmetry order of 120 including transformations that combine a reflection and a rotation...
(Ih) and the same vertex arrangement
Vertex arrangement
In geometry, a vertex arrangement is a set of points in space described by their relative positions. They can be described by their use in polytopes....
as a rhombic triacontahedron
Rhombic triacontahedron
In geometry, the rhombic triacontahedron is a convex polyhedron with 30 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. It is the polyhedral dual of the icosidodecahedron, and it is a zonohedron....
.
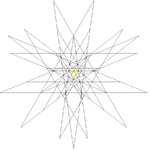
As a stellation
This polyhedronPolyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
is the first stellation
Stellation
Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...
of the icosidodecahedron
Icosidodecahedron
In geometry, an icosidodecahedron is a polyhedron with twenty triangular faces and twelve pentagonal faces. An icosidodecahedron has 30 identical vertices, with two triangles and two pentagons meeting at each, and 60 identical edges, each separating a triangle from a pentagon...
, and given as Wenninger model index 47.
The stellation facets for construction are: