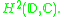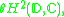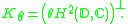Aleksandrov-Clark measure
Encyclopedia
In mathematics
, Aleksandrov–Clark (AC) measures are specially constructed measures named after the two mathematician
s, A. B. Aleksandrov and Douglas Clark, who discovered some of their deepest properties. The measures are also called either Aleksandrov measures, Clark measures, or occasionally spectral measures.
:
By virtue of Beurling's theorem, any shift-invariant subspace of this space is of the form
where is an inner function. As such, any invariant subspace of the adjoint of the shift is of the form
is an inner function. As such, any invariant subspace of the adjoint of the shift is of the form
We now define to be the shift operator compressed to
to be the shift operator compressed to 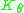 , that is
, that is
Clark noticed that all the one-dimensional perturbations of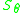 , which were also unitary maps, were of the form
, which were also unitary maps, were of the form
and related each such map to a measure,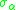 on the unit circle, via the Spectral theorem
on the unit circle, via the Spectral theorem
. This collection of measures, one for each on the unit circle
on the unit circle  , is then called the collection of AC measures associated with
, is then called the collection of AC measures associated with  .
.
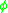 , of the unit disc,
, of the unit disc, 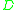 , we can construct a collection of functions,
, we can construct a collection of functions, 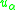 , given by
, given by

one for each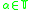 . Each of these functions is positive and harmonic, so by Herglotz' Theorem each is the Poisson integral of some positive measure
. Each of these functions is positive and harmonic, so by Herglotz' Theorem each is the Poisson integral of some positive measure 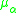 on
on  . This collection is the set of AC measures associated with
. This collection is the set of AC measures associated with 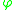 . It can be shown that the two definitions coincide for inner functions.
. It can be shown that the two definitions coincide for inner functions.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Aleksandrov–Clark (AC) measures are specially constructed measures named after the two mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
s, A. B. Aleksandrov and Douglas Clark, who discovered some of their deepest properties. The measures are also called either Aleksandrov measures, Clark measures, or occasionally spectral measures.
Construction of the measures
The original construction of Clark relates to one-dimensional perturbations of compressed shift operators on subspaces of the Hardy spaceHardy space
In complex analysis, the Hardy spaces Hp are certain spaces of holomorphic functions on the unit disk or upper half plane. They were introduced by Frigyes Riesz , who named them after G. H. Hardy, because of the paper...
:
By virtue of Beurling's theorem, any shift-invariant subspace of this space is of the form
where
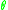 is an inner function. As such, any invariant subspace of the adjoint of the shift is of the form
is an inner function. As such, any invariant subspace of the adjoint of the shift is of the formWe now define
 to be the shift operator compressed to
to be the shift operator compressed to 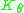 , that is
, that isClark noticed that all the one-dimensional perturbations of
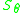 , which were also unitary maps, were of the form
, which were also unitary maps, were of the formand related each such map to a measure,
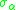 on the unit circle, via the Spectral theorem
on the unit circle, via the Spectral theoremSpectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
. This collection of measures, one for each
 on the unit circle
on the unit circle  , is then called the collection of AC measures associated with
, is then called the collection of AC measures associated with  .
.An alternative construction
The collection of measures may also be constructed for any analytic function (that is, not necessarily an inner function). Given an analytic self map,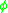 , of the unit disc,
, of the unit disc, 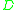 , we can construct a collection of functions,
, we can construct a collection of functions, 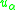 , given by
, given by
one for each
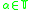 . Each of these functions is positive and harmonic, so by Herglotz' Theorem each is the Poisson integral of some positive measure
. Each of these functions is positive and harmonic, so by Herglotz' Theorem each is the Poisson integral of some positive measure 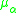 on
on  . This collection is the set of AC measures associated with
. This collection is the set of AC measures associated with 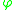 . It can be shown that the two definitions coincide for inner functions.
. It can be shown that the two definitions coincide for inner functions.