
Coarea formula
Encyclopedia
In the mathematical
field of geometric measure theory
, the coarea formula expresses the integral
of a function over an open set
in Euclidean space
in terms of the integral of the level set
s of another function. A special case is Fubini's theorem
, which says under suitable hypotheses that the integral of a function over the region enclosed by a rectangular box can be written as the iterated integral over the level sets of the coordinate functions. Another special case is integration in spherical coordinates, in which the integral of a function on Rn is related to the integral of the function over spherical shells: level sets of the radial function. The formula plays a decisive role in the modern study of isoperimetric problem
s.
For smooth function
s the formula is a result in multivariate calculus which follows from a simple change of variables
. More general forms of the formula for Lipschitz functions were first established by Herbert Federer
, and for Sobolev functions
by .
A precise statement of the formula is as follows. Suppose that Ω is an open set in Rn, and u is a real-valued Lipschitz function on Ω. Then, for an L1
function g,
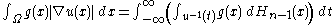
where Hn − 1 is the (n − 1)-dimensional Hausdorff measure
. In particular, by taking g to be one, this implies
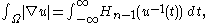
and conversely the latter equality implies the former by standard techniques in Lebesgue integration.
More generally, the coarea formula can be applied to Lipschitz functions u defined in Ω ⊂ Rn, taking on values in Rk where k < n. In this case, the following identity holds

where Jku is the k-dimensional Jacobian
of u.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of geometric measure theory
Geometric measure theory
In mathematics, geometric measure theory is the study of the geometric properties of the measures of sets , including such things as arc lengths and areas. It uses measure theory to generalize differential geometry to surfaces with mild singularities called rectifiable sets...
, the coarea formula expresses the integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
of a function over an open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
in terms of the integral of the level set
Level set
In mathematics, a level set of a real-valued function f of n variables is a set of the formthat is, a set where the function takes on a given constant value c....
s of another function. A special case is Fubini's theorem
Fubini's theorem
In mathematical analysis Fubini's theorem, named after Guido Fubini, is a result which gives conditions under which it is possible to compute a double integral using iterated integrals. As a consequence it allows the order of integration to be changed in iterated integrals.-Theorem...
, which says under suitable hypotheses that the integral of a function over the region enclosed by a rectangular box can be written as the iterated integral over the level sets of the coordinate functions. Another special case is integration in spherical coordinates, in which the integral of a function on Rn is related to the integral of the function over spherical shells: level sets of the radial function. The formula plays a decisive role in the modern study of isoperimetric problem
Isoperimetric problem
Isoperimetric problem may refer to:* Isoperimetric inequality* Any problem in calculus of variations...
s.
For smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s the formula is a result in multivariate calculus which follows from a simple change of variables
Change of variables
In mathematics, a change of variables is a basic technique used to simplify problems in which the original variables are replaced with new ones; the new and old variables being related in some specified way...
. More general forms of the formula for Lipschitz functions were first established by Herbert Federer
Herbert Federer
Herbert Federer was an American mathematician. He is one of the creators of geometric measure theory, at the meeting point of differential geometry and mathematical analysis.-Career:...
, and for Sobolev functions
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
by .
A precise statement of the formula is as follows. Suppose that Ω is an open set in Rn, and u is a real-valued Lipschitz function on Ω. Then, for an L1
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
function g,
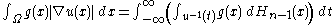
where Hn − 1 is the (n − 1)-dimensional Hausdorff measure
Hausdorff measure
In mathematics a Hausdorff measure is a type of outer measure, named for Felix Hausdorff, that assigns a number in [0,∞] to each set in Rn or, more generally, in any metric space. The zero dimensional Hausdorff measure is the number of points in the set or ∞ if the set is infinite...
. In particular, by taking g to be one, this implies
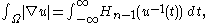
and conversely the latter equality implies the former by standard techniques in Lebesgue integration.
More generally, the coarea formula can be applied to Lipschitz functions u defined in Ω ⊂ Rn, taking on values in Rk where k < n. In this case, the following identity holds

where Jku is the k-dimensional Jacobian
Jacobian
In vector calculus, the Jacobian matrix is the matrix of all first-order partial derivatives of a vector- or scalar-valued function with respect to another vector. Suppose F : Rn → Rm is a function from Euclidean n-space to Euclidean m-space...
of u.
Applications
- Taking u(x) = |x − x0| gives the formula for integration in spherical coordinates of an integrable function ƒ:
-
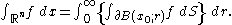
- Combining the coarea formula with the isoperimetric inequality gives a proof of the Sobolev inequalitySobolev inequalityIn mathematics, there is in mathematical analysis a class of Sobolev inequalities, relating norms including those of Sobolev spaces. These are used to prove the Sobolev embedding theorem, giving inclusions between certain Sobolev spaces, and the Rellich–Kondrachov theorem showing that under...
for W1,1 with best constant:
- Combining the coarea formula with the isoperimetric inequality gives a proof of the Sobolev inequality

- where ω −1/n is the volume of the unit ball in Rn.

