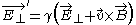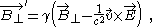Classical electromagnetism and special relativity
Encyclopedia
The theory of special relativity
plays an important role in the modern theory of classical electromagnetism
. First of all, it gives formulas for how electromagnetic objects, in particular the electric
and magnetic field
s, are altered under a Lorentz transformation
from one inertial frame of reference to another. Secondly, it sheds light on the relationship between electricity and magnetism, showing that frame of reference determines if an observation follows electrostatic or magnetic laws. Third, it motivates a compact and convenient notation for the laws of electromagnetism, namely the "manifestly covariant" tensor form.
where
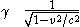
is called the Lorentz factor
and c is the speed of light
in free space. The inverse transformations are the same except v → −v.
An equivalent, alternative expression is:
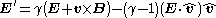
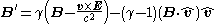
where :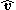 is velocity's unit vector.
is velocity's unit vector.
If a particle of charge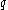 moves with velocity
moves with velocity  with respect to frame S, then the Lorentz force in frame S is:
with respect to frame S, then the Lorentz force in frame S is:
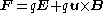
In frame S', the Lorentz force is:
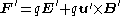
If S and S' have aligned axes then:
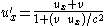
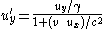
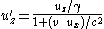
A derivation for the transformation of the Lorentz force for the particular case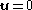 is given here. A more general one can be seen here.
is given here. A more general one can be seen here.
Component by component, for relative motion along the x-axis, this works out to be the following, in SI units:
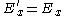
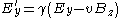

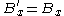
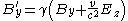
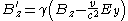
and in Gaussian-cgs units
, the transformation is given by:
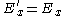
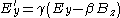
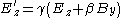
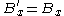
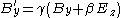
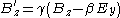
where .
.
The claim that the transformation rules for E and B take this particular form is equivalent to the claim that the electromagnetic tensor
(defined below) is a covariant tensor.
are taken into account. The Feynman Lectures on Physics
(vol. 2, ch. 13-6) uses this method to derive the "magnetic" force on a moving charge next to a current-carrying wire. See also Haskell, Landau, and Field.
. Indeed, the entire electromagnetic field can be encoded in a single rank-2 tensor called the electromagnetic tensor
; see below.
If a conductor moves with a constant velocity through the field of a stationary magnet, eddy current
s will be produced due to a magnetic force on the electrons in the conductor. In the rest frame of the conductor, on the other hand, the magnet will be moving and the conductor stationary. Classical electromagnetic theory predicts that precisely the same microscopic eddy currents will be produced, but they will be due to an electric force.
, the electric and magnetic fields combine into the covariant electromagnetic tensor
: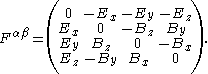
The charge
and current
, meanwhile, combine into a four-vector
called the four-current
: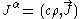
where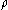 is the charge density,
is the charge density, 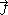 is the current density, and c is the speed of light
is the current density, and c is the speed of light
.
With these definitions, Maxwell's equations
take the following manifestly covariant form:
where F αβ is the electromagnetic tensor
, J α is the 4-current, є αβγδ is the Levi-Civita symbol
(a mathematical construct), and the indices behave according to the Einstein summation convention.
The first tensor equation is an expression of the two inhomogeneous Maxwell's equations, Gauss's Law
and Ampere's Law
(with Maxwell's correction). The second equation is an expression of the homogenous equations, Faraday's law of induction
and Gauss's law for magnetism.
Another covariant electromagnetic object is the electromagnetic stress-energy tensor, a covariant rank-2 tensor which includes the Poynting vector
, Maxwell stress tensor
, and electromagnetic energy density. Yet another is the four-potential, a four-vector combining the electric potential
and magnetic vector potential.
A particularly convenient gauge choice
in a relativistic setting is the Lorenz gauge condition
, which in terms of the four-potential takes the covariant form:
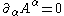
In the Lorenz gauge, Maxwell's equations can be written as (in cgs):

where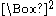 denotes the d'Alembertian.
denotes the d'Alembertian.
For a more comprehensive presentation of these topics, see Covariant formulation of classical electromagnetism.
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
plays an important role in the modern theory of classical electromagnetism
Classical electromagnetism
Classical electromagnetism is a branch of theoretical physics that studies consequences of the electromagnetic forces between electric charges and currents...
. First of all, it gives formulas for how electromagnetic objects, in particular the electric
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
and magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
s, are altered under a Lorentz transformation
Lorentz transformation
In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik...
from one inertial frame of reference to another. Secondly, it sheds light on the relationship between electricity and magnetism, showing that frame of reference determines if an observation follows electrostatic or magnetic laws. Third, it motivates a compact and convenient notation for the laws of electromagnetism, namely the "manifestly covariant" tensor form.
Joules-Bernoulli equation for fields and forces
This equation considers two inertial frames. As notation, the field variables in one frame are unprimed, and in a frame moving relative to the unprimed frame at velocity v, the fields are denoted with primes. In addition, the fields parallel to the velocity v are denoted by while the fields perpendicular to v are denoted as . In these two frames moving at relative velocity v, the E-fields and B-fields are related by:where
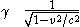
is called the Lorentz factor
Lorentz factor
The Lorentz factor or Lorentz term appears in several equations in special relativity, including time dilation, length contraction, and the relativistic mass formula. Because of its ubiquity, physicists generally represent it with the shorthand symbol γ . It gets its name from its earlier...
and c is the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
in free space. The inverse transformations are the same except v → −v.
An equivalent, alternative expression is:
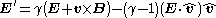
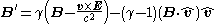
where :
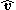 is velocity's unit vector.
is velocity's unit vector.If a particle of charge
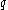 moves with velocity
moves with velocity  with respect to frame S, then the Lorentz force in frame S is:
with respect to frame S, then the Lorentz force in frame S is: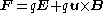
In frame S', the Lorentz force is:
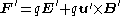
If S and S' have aligned axes then:
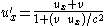
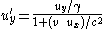
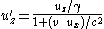
A derivation for the transformation of the Lorentz force for the particular case
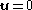 is given here. A more general one can be seen here.
is given here. A more general one can be seen here.Component by component, for relative motion along the x-axis, this works out to be the following, in SI units:
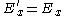
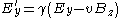

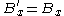
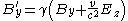
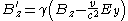
and in Gaussian-cgs units
Gaussian units
Gaussian units comprise a metric system of physical units. This system is the most common of the several electromagnetic unit systems based on cgs units. It is also called the Gaussian unit system, Gaussian-cgs units, or often just cgs units...
, the transformation is given by:
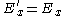
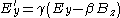
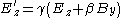
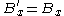
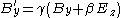
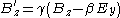
where
 .
.The claim that the transformation rules for E and B take this particular form is equivalent to the claim that the electromagnetic tensor
Electromagnetic tensor
The electromagnetic tensor or electromagnetic field tensor is a mathematical object that describes the electromagnetic field of a physical system in Maxwell's theory of electromagnetism...
(defined below) is a covariant tensor.
Relationship between electricity and magnetism
- "One part of the force between moving charges we call the magnetic force. It is really one aspect of an electrical effect."
- - Feynman LecturesThe Feynman Lectures on PhysicsThe Feynman Lectures on Physics is a 1964 physics textbook by Richard P. Feynman, Robert B. Leighton and Matthew Sands, based upon the lectures given by Feynman to undergraduate students at the California Institute of Technology in 1961–63. It includes lectures on mathematics, electromagnetism,...
vol. 2, ch. 1-1
Deriving magnetism from electrostatics
The chosen reference frame determines if an electromagnetic phenomenon is viewed as an effect of electrostatics or magnetism. Authors usually derive magnetism from electrostatics when special relativity and charge invarianceCharge invariance
Charge invariance refers to the fixed electrostatic potential of a particle, regardless of speed. For example, an electron has a specific rest charge. Accelerate that electron, and the charge remains the same . The key word here is relativistic...
are taken into account. The Feynman Lectures on Physics
The Feynman Lectures on Physics
The Feynman Lectures on Physics is a 1964 physics textbook by Richard P. Feynman, Robert B. Leighton and Matthew Sands, based upon the lectures given by Feynman to undergraduate students at the California Institute of Technology in 1961–63. It includes lectures on mathematics, electromagnetism,...
(vol. 2, ch. 13-6) uses this method to derive the "magnetic" force on a moving charge next to a current-carrying wire. See also Haskell, Landau, and Field.
Fields intermix in different frames
The above transformation rules show that the electric field in one frame contributes to the magnetic field in another frame, and vice versa. This is often described by saying that the electric field and magnetic field are two interrelated aspects of a single object, called the electromagnetic fieldElectromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
. Indeed, the entire electromagnetic field can be encoded in a single rank-2 tensor called the electromagnetic tensor
Electromagnetic tensor
The electromagnetic tensor or electromagnetic field tensor is a mathematical object that describes the electromagnetic field of a physical system in Maxwell's theory of electromagnetism...
; see below.
Moving magnet and conductor problem
A famous example of the intermixing of electric and magnetic phenomena in different frames of reference is called the "moving magnet and conductor problem", cited by Einstein in his 1905 paper on Special Relativity.If a conductor moves with a constant velocity through the field of a stationary magnet, eddy current
Eddy current
Eddy currents are electric currents induced in conductors when a conductor is exposed to a changing magnetic field; due to relative motion of the field source and conductor or due to variations of the field with time. This can cause a circulating flow of electrons, or current, within the body of...
s will be produced due to a magnetic force on the electrons in the conductor. In the rest frame of the conductor, on the other hand, the magnet will be moving and the conductor stationary. Classical electromagnetic theory predicts that precisely the same microscopic eddy currents will be produced, but they will be due to an electric force.
Covariant formulation in vacuum
The laws and objects in classical electromagnetism can be written in a form which is manifestly covariant. Here, this is only done so for vacuum (or for the microscopic Maxwell equations, not using macroscopic descriptions of materials such as electric permittivity). In cgs-Gaussian unitsGaussian units
Gaussian units comprise a metric system of physical units. This system is the most common of the several electromagnetic unit systems based on cgs units. It is also called the Gaussian unit system, Gaussian-cgs units, or often just cgs units...
, the electric and magnetic fields combine into the covariant electromagnetic tensor
Electromagnetic tensor
The electromagnetic tensor or electromagnetic field tensor is a mathematical object that describes the electromagnetic field of a physical system in Maxwell's theory of electromagnetism...
:
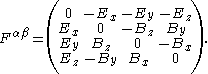
The charge
Charge (physics)
In physics, a charge may refer to one of many different quantities, such as the electric charge in electromagnetism or the color charge in quantum chromodynamics. Charges are associated with conserved quantum numbers.-Formal definition:...
and current
Electric current
Electric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire...
, meanwhile, combine into a four-vector
Four-vector
In the theory of relativity, a four-vector is a vector in a four-dimensional real vector space, called Minkowski space. It differs from a vector in that it can be transformed by Lorentz transformations. The usage of the four-vector name tacitly assumes that its components refer to a standard basis...
called the four-current
Four-current
In special and general relativity, the four-current is the Lorentz covariant four-vector that replaces the electromagnetic current density, or indeed any conventional charge current density...
:
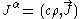
where
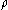 is the charge density,
is the charge density, 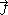 is the current density, and c is the speed of light
is the current density, and c is the speed of lightSpeed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
.
With these definitions, Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
take the following manifestly covariant form:

where F αβ is the electromagnetic tensor
Electromagnetic tensor
The electromagnetic tensor or electromagnetic field tensor is a mathematical object that describes the electromagnetic field of a physical system in Maxwell's theory of electromagnetism...
, J α is the 4-current, є αβγδ is the Levi-Civita symbol
Levi-Civita symbol
The Levi-Civita symbol, also called the permutation symbol, antisymmetric symbol, or alternating symbol, is a mathematical symbol used in particular in tensor calculus...
(a mathematical construct), and the indices behave according to the Einstein summation convention.
The first tensor equation is an expression of the two inhomogeneous Maxwell's equations, Gauss's Law
Gauss's law
In physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:...
and Ampere's Law
Ampère's law
In classical electromagnetism, Ampère's circuital law, discovered by André-Marie Ampère in 1826, relates the integrated magnetic field around a closed loop to the electric current passing through the loop...
(with Maxwell's correction). The second equation is an expression of the homogenous equations, Faraday's law of induction
Faraday's law of induction
Faraday's law of induction dates from the 1830s, and is a basic law of electromagnetism relating to the operating principles of transformers, inductors, and many types of electrical motors and generators...
and Gauss's law for magnetism.
Another covariant electromagnetic object is the electromagnetic stress-energy tensor, a covariant rank-2 tensor which includes the Poynting vector
Poynting vector
In physics, the Poynting vector can be thought of as representing the directional energy flux density of an electromagnetic field. It is named after its inventor John Henry Poynting. Oliver Heaviside and Nikolay Umov independently co-invented the Poynting vector...
, Maxwell stress tensor
Maxwell stress tensor
The Maxwell Stress Tensor is a mathematical object in physics, more precisely it is a second rank tensor used in classical electromagnetism to represent the interaction between electric/magnetic forces and mechanical momentum...
, and electromagnetic energy density. Yet another is the four-potential, a four-vector combining the electric potential
Electric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
and magnetic vector potential.
A particularly convenient gauge choice
Gauge fixing
In the physics of gauge theories, gauge fixing denotes a mathematical procedure for coping with redundant degrees of freedom in field variables. By definition, a gauge theory represents each physically distinct configuration of the system as an equivalence class of detailed local field...
in a relativistic setting is the Lorenz gauge condition
Lorenz gauge condition
In electromagnetism, the Lorenz gauge or Lorenz gauge condition is a partial gauge fixing of the electromagnetic vector potential. The condition is that \partial_\mu A^\mu=0...
, which in terms of the four-potential takes the covariant form:
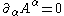
In the Lorenz gauge, Maxwell's equations can be written as (in cgs):

where
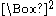 denotes the d'Alembertian.
denotes the d'Alembertian.For a more comprehensive presentation of these topics, see Covariant formulation of classical electromagnetism.