Chebotarev's density theorem
Encyclopedia
Chebotarev's density theorem in algebraic number theory
describes statistically the splitting of primes
in a given Galois extension
K of the field Q of rational number
s. Generally speaking, a prime integer will factor into several ideal primes
in the ring of algebraic integer
s of K. There are only finitely many patterns of splitting that may occur. Although the full description of the splitting of every prime p in a general Galois extension is a major unsolved problem, the Chebotarev density theorem says that the frequency of the occurrence of a given pattern, for all primes p less than a large integer N, tends to a certain limit as N goes to infinity. It was proved by Nikolai Chebotaryov
in his thesis in 1922.
A special case that is easier to state says that if K is an algebraic number field
which is a Galois extension of Q of degree n, then the prime numbers that completely split in K have density
among all primes. More generally, splitting behavior can be specified by assigning to (almost) every prime number an invariant, its Frobenius element, which strictly is a representative of a well-defined conjugacy class
in the Galois group
Then the theorem says that the asymptotic distribution of these invariants is uniform over the group, so that a conjugacy class with k elements occurs with frequency asymptotic to
first introduced the notion of complex integers
Z[i], he observed that the ordinary prime numbers may factor further in this new set of integers. In fact, if a prime p is congruent to 1 mod 4, then it factors into a product of two distinct prime gaussian integers, or "splits completely"; if p is congruent to 3 mod 4, then it remains prime, or is "inert"; and if p is 2 then it becomes a product of the square of the prime (1+i) and the invertible gaussian integer -i; we say that 2 "ramifies". For instance,
From this description, it appears that as one considers larger and larger primes, the frequency of a prime splitting completely approaches 1/2, and likewise for the primes that remain primes in Z[i]. Dirichlet's theorem on arithmetic progressions
demonstrates that this is indeed the case. Even though the prime numbers themselves appear rather erratically, splitting of the primes in the extension
follows a simple statistical law.
Similar statistical laws also hold for splitting of primes in the cyclotomic extensions
, obtained from the field of rational numbers by adjoining a primitive root of unity of a given order. For example, the ordinary integer primes group into four classes, each with probability 1/4, according to their pattern of splitting in the ring of integers corresponding to the 8th roots of unity.
In this case, the field extension has degree 4 and is abelian
, with the Galois group isomorphic to the Klein four-group
. It turned out that the Galois group of the extension plays a key role in the pattern of splitting of primes. Georg Frobenius established the framework for investigating this pattern and proved a special case of the theorem. The general statement was proved by Nikolai Grigoryevich Chebotaryov in 1922.
. A quantitative form of Dirichlet's theorem states that if N≥2 is an integer and a is coprime
to N, then the proportion of the primes p congruent to a mod N is asymptotic to 1/n, where n=φ(N) is the Euler totient function. This is a special case of the Chebotarev density theorem for the Nth cyclotomic field
K. Indeed, the Galois group of K/Q is abelian and can be canonically identified with the group of invertible residue classes mod N. The splitting invariant of a prime p not dividing N is simply its residue class because the number of distinct primes into which p splits is φ(N)/m, where m is multiplicative order of p modulo N; hence by the Chebotarev density theorem, primes are asymptotically uniformly distributed among different residue classes coprime to N.
of the rational number field Q, and P(t) a monic integer polynomial such that K is a splitting field
of P. It makes sense to factorise P modulo a prime number p. Its 'splitting type' is the list of degrees of irreducible factors of P mod p, i.e. P factorizes in some fashion over the prime field Fp. If n is the degree of P, then the splitting type is a partition Π of n. Considering also the Galois group
G of K over Q, each g in G is a permutation of the roots of P in K; in other words by choosing an ordering of α and its algebraic conjugates, G is faithfully represented as a subgroup of the symmetric group
Sn. We can write g by means of its cycle representation, which gives a 'cycle type' c(g), again a partition of n.
The theorem of Frobenius states that for any given choice of Π the primes p for which the splitting type of P mod p is Π has a natural density
δ, with δ equal to the proportion of g in G that have cycle type Π.
The statement of the more general Chebotarev theorem is in terms of the Frobenius element of a prime (ideal), which is in fact an associated conjugacy class
C of elements of the Galois group
G. If we fix C then the theorem says that asymptotically a proportion |C|/|G| of primes have associated Frobenius element as C. When G is abelian the classes of course each have size 1. For the case of a non-abelian group of order 6 they have size 1, 2 and 3, and there are correspondingly (for example) 50% of primes p that have an order 2 element as their Frobenius. So these primes have residue degree 2, so they split into exactly three prime ideals in a degree 6 extension of Q with it as Galois group.
This reduces to the finite case when L / K is finite (the Haar measure is then just the counting measure).
A consequence of this version of the theorem is that the Frobenius elements of the unramified primes of L are dense in G.
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
describes statistically the splitting of primes
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
in a given Galois extension
Galois extension
In mathematics, a Galois extension is an algebraic field extension E/F satisfying certain conditions ; one also says that the extension is Galois. The significance of being a Galois extension is that the extension has a Galois group and obeys the fundamental theorem of Galois theory.The definition...
K of the field Q of rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s. Generally speaking, a prime integer will factor into several ideal primes
Ideal number
In number theory an ideal number is an algebraic integer which represents an ideal in the ring of integers of a number field; the idea was developed by Ernst Kummer, and led to Richard Dedekind's definition of ideals for rings...
in the ring of algebraic integer
Algebraic integer
In number theory, an algebraic integer is a complex number that is a root of some monic polynomial with coefficients in . The set of all algebraic integers is closed under addition and multiplication and therefore is a subring of complex numbers denoted by A...
s of K. There are only finitely many patterns of splitting that may occur. Although the full description of the splitting of every prime p in a general Galois extension is a major unsolved problem, the Chebotarev density theorem says that the frequency of the occurrence of a given pattern, for all primes p less than a large integer N, tends to a certain limit as N goes to infinity. It was proved by Nikolai Chebotaryov
Nikolai Chebotaryov
Nikolai Chebotaryov was a noted Russian and Soviet mathematician. He is best known for the Chebotaryov density theorem....
in his thesis in 1922.
A special case that is easier to state says that if K is an algebraic number field
Algebraic number field
In mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
which is a Galois extension of Q of degree n, then the prime numbers that completely split in K have density
- 1/n
among all primes. More generally, splitting behavior can be specified by assigning to (almost) every prime number an invariant, its Frobenius element, which strictly is a representative of a well-defined conjugacy class
Conjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
in the Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
- Gal(K/Q).
Then the theorem says that the asymptotic distribution of these invariants is uniform over the group, so that a conjugacy class with k elements occurs with frequency asymptotic to
- k/n.
History and motivation
When Carl Friedrich GaussCarl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
first introduced the notion of complex integers
Gaussian integer
In number theory, a Gaussian integer is a complex number whose real and imaginary part are both integers. The Gaussian integers, with ordinary addition and multiplication of complex numbers, form an integral domain, usually written as Z[i]. The Gaussian integers are a special case of the quadratic...
Z[i], he observed that the ordinary prime numbers may factor further in this new set of integers. In fact, if a prime p is congruent to 1 mod 4, then it factors into a product of two distinct prime gaussian integers, or "splits completely"; if p is congruent to 3 mod 4, then it remains prime, or is "inert"; and if p is 2 then it becomes a product of the square of the prime (1+i) and the invertible gaussian integer -i; we say that 2 "ramifies". For instance,
-
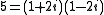splits completely; -
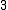is inert; -
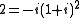ramifies.
From this description, it appears that as one considers larger and larger primes, the frequency of a prime splitting completely approaches 1/2, and likewise for the primes that remain primes in Z[i]. Dirichlet's theorem on arithmetic progressions
Dirichlet's theorem on arithmetic progressions
In number theory, Dirichlet's theorem, also called the Dirichlet prime number theorem, states that for any two positive coprime integers a and d, there are infinitely many primes of the form a + nd, where n ≥ 0. In other words, there are infinitely many primes which are...
demonstrates that this is indeed the case. Even though the prime numbers themselves appear rather erratically, splitting of the primes in the extension
follows a simple statistical law.
Similar statistical laws also hold for splitting of primes in the cyclotomic extensions
Cyclotomic field
In number theory, a cyclotomic field is a number field obtained by adjoining a complex primitive root of unity to Q, the field of rational numbers...
, obtained from the field of rational numbers by adjoining a primitive root of unity of a given order. For example, the ordinary integer primes group into four classes, each with probability 1/4, according to their pattern of splitting in the ring of integers corresponding to the 8th roots of unity.
In this case, the field extension has degree 4 and is abelian
Abelian extension
In abstract algebra, an abelian extension is a Galois extension whose Galois group is abelian. When the Galois group is a cyclic group, we have a cyclic extension. More generally, a Galois extension is called solvable if its Galois group is solvable....
, with the Galois group isomorphic to the Klein four-group
Klein four-group
In mathematics, the Klein four-group is the group Z2 × Z2, the direct product of two copies of the cyclic group of order 2...
. It turned out that the Galois group of the extension plays a key role in the pattern of splitting of primes. Georg Frobenius established the framework for investigating this pattern and proved a special case of the theorem. The general statement was proved by Nikolai Grigoryevich Chebotaryov in 1922.
Relation with Dirichlet's theorem
The Chebotarev density theorem may be viewed as a generalisation of Dirichlet's theorem on arithmetic progressionsDirichlet's theorem on arithmetic progressions
In number theory, Dirichlet's theorem, also called the Dirichlet prime number theorem, states that for any two positive coprime integers a and d, there are infinitely many primes of the form a + nd, where n ≥ 0. In other words, there are infinitely many primes which are...
. A quantitative form of Dirichlet's theorem states that if N≥2 is an integer and a is coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
to N, then the proportion of the primes p congruent to a mod N is asymptotic to 1/n, where n=φ(N) is the Euler totient function. This is a special case of the Chebotarev density theorem for the Nth cyclotomic field
Cyclotomic field
In number theory, a cyclotomic field is a number field obtained by adjoining a complex primitive root of unity to Q, the field of rational numbers...
K. Indeed, the Galois group of K/Q is abelian and can be canonically identified with the group of invertible residue classes mod N. The splitting invariant of a prime p not dividing N is simply its residue class because the number of distinct primes into which p splits is φ(N)/m, where m is multiplicative order of p modulo N; hence by the Chebotarev density theorem, primes are asymptotically uniformly distributed among different residue classes coprime to N.
Formulation
The cited paper of Lenstra and Stevenhagen gives an earlier result of Frobenius in this area. Suppose K is a Galois extensionGalois extension
In mathematics, a Galois extension is an algebraic field extension E/F satisfying certain conditions ; one also says that the extension is Galois. The significance of being a Galois extension is that the extension has a Galois group and obeys the fundamental theorem of Galois theory.The definition...
of the rational number field Q, and P(t) a monic integer polynomial such that K is a splitting field
Splitting field
In abstract algebra, a splitting field of a polynomial with coefficients in a field is a smallest field extension of that field over which the polynomial factors into linear factors.-Definition:...
of P. It makes sense to factorise P modulo a prime number p. Its 'splitting type' is the list of degrees of irreducible factors of P mod p, i.e. P factorizes in some fashion over the prime field Fp. If n is the degree of P, then the splitting type is a partition Π of n. Considering also the Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
G of K over Q, each g in G is a permutation of the roots of P in K; in other words by choosing an ordering of α and its algebraic conjugates, G is faithfully represented as a subgroup of the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
Sn. We can write g by means of its cycle representation, which gives a 'cycle type' c(g), again a partition of n.
The theorem of Frobenius states that for any given choice of Π the primes p for which the splitting type of P mod p is Π has a natural density
Natural density
In number theory, asymptotic density is one of the possibilities to measure how large a subset of the set of natural numbers is....
δ, with δ equal to the proportion of g in G that have cycle type Π.
The statement of the more general Chebotarev theorem is in terms of the Frobenius element of a prime (ideal), which is in fact an associated conjugacy class
Conjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
C of elements of the Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
G. If we fix C then the theorem says that asymptotically a proportion |C|/|G| of primes have associated Frobenius element as C. When G is abelian the classes of course each have size 1. For the case of a non-abelian group of order 6 they have size 1, 2 and 3, and there are correspondingly (for example) 50% of primes p that have an order 2 element as their Frobenius. So these primes have residue degree 2, so they split into exactly three prime ideals in a degree 6 extension of Q with it as Galois group.
Statement
Let L be a finite Galois extension of a number field K with Galois group G. Let X be a subset of G that is stable under conjugation. The set of primes v of K that are unramified in L and whose associated Frobenius conjugacy class Fv is contained in X has densityInfinite extensions
The statement of the Chebotarev density theorem can be generalized to the case of an infinite Galois extension L / K that is unramified outside a finite set S of primes of K (i.e. if there is a finite set S of primes of K such that any prime of K not in S is unramified in the extension L / K). In this case, the Galois group G of L / K is a profinite group equipped with the Krull topology. Since G is compact in this topology, there is a unique Haar measure μ on G. For every prime v of K not in S there is an associated Frobenius conjugacy class Fv. The Chebotarev density theorem in this situation can be stated as follows:- Let X be a subset of G that is stable under conjugation and whose boundary has Haar measure zero. Then, the set of primes v of K not in S such that Fv ⊆ X has density
This reduces to the finite case when L / K is finite (the Haar measure is then just the counting measure).
A consequence of this version of the theorem is that the Frobenius elements of the unramified primes of L are dense in G.