Cayley's theorem
Encyclopedia
In group theory
, Cayley's theorem, named in honor of Arthur Cayley
, states that every group
G is isomorphic
to a subgroup
of the symmetric group
acting on G. This can be understood as an example of the group action
of G on the elements of G.
A permutation
of a set G is any bijective function
taking G onto G; and the set of all such functions forms a group under function composition
, called the symmetric group on G, and written as Sym(G).
Cayley's theorem puts all groups on the same footing, by considering any group (including infinite groups such as (R,+)) as a permutation group
of some underlying set. Thus, theorems which are true for permutation groups are true for groups in general.
attributes the theorem
to Jordan,
Eric Nummela
nonetheless argues that the standard name—"Cayley's Theorem"—is in fact appropriate. Cayley, in his original 1854 paper,
showed that the correspondence in the theorem is one-to-one, but he failed to explicitly show it was a homomorphism (and thus an isomorphism). However, Nummela notes that Cayley made this result known to the mathematical community at the time, thus predating Jordan by 16 years or so.
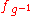. So multiplication by g acts as a bijective function. Thus, fg is a permutation of G, and so is a member of Sym(G).
The set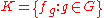
is a subgroup of Sym(G) which is isomorphic to G. The fastest way to establish this is to consider the function T : G → Sym(G) with T(g) = fg for every g in G. T is a group homomorphism
because (using "•" for composition in Sym(G)):
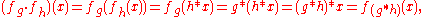
for all x in G, and hence: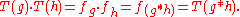
The homomorphism T is also injective since T(g) = idG (the identity element of Sym(G)) implies that g*x = x for all x in G, and taking x to be the identity element e of G yields g = g*e = e. Alternatively, T is also injective since, if g*x=g*x implies g=g' (by post-multiplying with the inverse of x, which exists because G is a group).
Thus G is isomorphic to the image of T, which is the subgroup K.
T is sometimes called the regular representation of G.
s. We consider the group
as a G-set, which can be shown to have permutation representation, say 
.
Firstly, suppose
with 
. Then the group action is 
by classification of G-orbits
(also known as the orbit-stabilizer theorem).
Now, the representation is faithful if
is injective, that is, if the kernel of 
is trivial. Suppose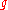 
∈ ker 
Then, 
by the equivalence of the permutation representation and the group action. But since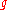 
∈ ker 
, 
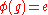and thus ker 
is trivial. Then im 
and thus the result follows by use of the first isomorphism theorem.
of the subgroup generated by the element.
Z3 = {0,1,2} with addition modulo 3; group element 0 corresponds to the identity permutation e, group element 1 to permutation (123), and group element 2 to permutation (132). E.g. 1 + 1 = 2 corresponds to (123)(123)=(132).
Z4 = {0,1,2,3} with addition modulo 4; the elements correspond to e, (1234), (13)(24), (1432).
The elements of Klein four-group
{e, a, b, c} correspond to e, (12)(34), (13)(24), and (14)(23).
S3 (dihedral group of order 6
) is the group of all permutations of 3 objects, but also a permutation group of the 6 group elements:
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, Cayley's theorem, named in honor of Arthur Cayley
Arthur Cayley
Arthur Cayley F.R.S. was a British mathematician. He helped found the modern British school of pure mathematics....
, states that every group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G is isomorphic
Group isomorphism
In abstract algebra, a group isomorphism is a function between two groups that sets up a one-to-one correspondence between the elements of the groups in a way that respects the given group operations. If there exists an isomorphism between two groups, then the groups are called isomorphic...
to a subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
acting on G. This can be understood as an example of the group action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of G on the elements of G.
A permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
of a set G is any bijective function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
taking G onto G; and the set of all such functions forms a group under function composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
, called the symmetric group on G, and written as Sym(G).
Cayley's theorem puts all groups on the same footing, by considering any group (including infinite groups such as (R,+)) as a permutation group
Permutation group
In mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
of some underlying set. Thus, theorems which are true for permutation groups are true for groups in general.
History
Although Burnsideattributes the theorem
to Jordan,
Eric Nummela
nonetheless argues that the standard name—"Cayley's Theorem"—is in fact appropriate. Cayley, in his original 1854 paper,
showed that the correspondence in the theorem is one-to-one, but he failed to explicitly show it was a homomorphism (and thus an isomorphism). However, Nummela notes that Cayley made this result known to the mathematical community at the time, thus predating Jordan by 16 years or so.
Proof of the theorem
Where g is any element of G, consider the function fg : G → G, defined by fg(x) = g*x. By the existence of inverses, this function has a two-sided inverse,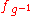. So multiplication by g acts as a bijective function. Thus, fg is a permutation of G, and so is a member of Sym(G).The set
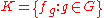is a subgroup of Sym(G) which is isomorphic to G. The fastest way to establish this is to consider the function T : G → Sym(G) with T(g) = fg for every g in G. T is a group homomorphismGroup homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
because (using "•" for composition in Sym(G)):
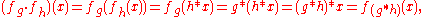
for all x in G, and hence:
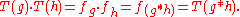
The homomorphism T is also injective since T(g) = idG (the identity element of Sym(G)) implies that g*x = x for all x in G, and taking x to be the identity element e of G yields g = g*e = e. Alternatively, T is also injective since, if g*x=g*x implies g=g' (by post-multiplying with the inverse of x, which exists because G is a group).
Thus G is isomorphic to the image of T, which is the subgroup K.
T is sometimes called the regular representation of G.
Alternative setting of proof
An alternative setting uses the language of group actionGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
s. We consider the group
as a G-set, which can be shown to have permutation representation, say .Firstly, suppose
with . Then the group action is by classification of G-orbitsGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
(also known as the orbit-stabilizer theorem).
Now, the representation is faithful if
is injective, that is, if the kernel of is trivial. Suppose 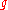∈ ker Then, by the equivalence of the permutation representation and the group action. But since 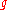∈ ker , 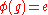and thus ker is trivial. Then im and thus the result follows by use of the first isomorphism theorem.Remarks on the regular group representation
The identity group element corresponds to the identity permutation. All other group elements correspond to a permutation that does not leave any element unchanged. Since this also applies for powers of a group element, lower than the order of that element, each element corresponds to a permutation which consists of cycles which are of the same length: this length is the order of that element. The elements in each cycle form a left cosetCoset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
of the subgroup generated by the element.
Examples of the regular group representation
Z2 = {0,1} with addition modulo 2; group element 0 corresponds to the identity permutation e, group element 1 to permutation (12).Z3 = {0,1,2} with addition modulo 3; group element 0 corresponds to the identity permutation e, group element 1 to permutation (123), and group element 2 to permutation (132). E.g. 1 + 1 = 2 corresponds to (123)(123)=(132).
Z4 = {0,1,2,3} with addition modulo 4; the elements correspond to e, (1234), (13)(24), (1432).
The elements of Klein four-group
Klein four-group
In mathematics, the Klein four-group is the group Z2 × Z2, the direct product of two copies of the cyclic group of order 2...
{e, a, b, c} correspond to e, (12)(34), (13)(24), and (14)(23).
S3 (dihedral group of order 6
Dihedral group of order 6
The smallest non-abelian group has 6 elements. It is a dihedral group with notation D3 and the symmetric group of degree 3, with notation S3....
) is the group of all permutations of 3 objects, but also a permutation group of the 6 group elements:
| * | e | a | b | c | d | f | permutation |
|---|---|---|---|---|---|---|---|
| e | e | a | b | c | d | f | e |
| a | a | e | d | f | b | c | (12)(35)(46) |
| b | b | f | e | d | c | a | (13)(26)(45) |
| c | c | d | f | e | a | b | (14)(25)(36) |
| d | d | c | a | b | f | e | (156)(243) |
| f | f | b | c | a | e | d | (165)(234) |
See also
- Containment orderContainment orderIn the mathematical field of order theory, a containment order is the partial order that arises as the subset-containment relation on some collection of objects. In a simple way, every poset P = is a containment order...
, a similar result in order theory - Frucht's theoremFrucht's theoremFrucht's theorem is a theorem in algebraic graph theory conjectured by Dénes Kőnig in 1936 and proved by Robert Frucht in 1939. It states that every finite group is the group of symmetries of a finite undirected graph...
, every group is the automorphism group of a graph - Yoneda lemmaYoneda lemmaIn mathematics, specifically in category theory, the Yoneda lemma is an abstract result on functors of the type morphisms into a fixed object. It is a vast generalisation of Cayley's theorem from group theory...
, an analogue of Cayley's theorem in category theory