
Cauchy's integral theorem
Encyclopedia
In mathematics
, the Cauchy integral theorem (also known as the Cauchy–Goursat theorem) in complex analysis
, named after Augustin-Louis Cauchy, is an important statement about line integral
s for holomorphic function
s in the complex plane
. Essentially, it says that if two different paths connect the same two points, and a function is holomorphic everywhere "in between" the two paths, then the two path integrals of the function will be the same.
The theorem is usually formulated for closed paths as follows: let U be an open subset of C which is simply connected, let f : U → C be a holomorphic function, and let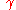 be a rectifiable path in U whose start point is equal to its end point. Then
be a rectifiable path in U whose start point is equal to its end point. Then
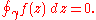
A precise (homology
) version can be stated using winding number
s. The winding number of a closed curve around a point 'a' not on the curve is the integral of 1/(2 i)f(z), where f(z) = 1/(z − a) around the curve. It is an integer
.
Briefly, the path integral along a Jordan curve of a function holomorphic in the interior of the curve, is zero. Instead of a single closed path we can consider a linear combination of closed path where the scalars are integers. Such a combination is called a closed chain and one defines integral along the chain as the linear combination of integrals over individual paths. A closed chain is called a cycle in a region if it is homologous to zero in the region, that is the winding number, expressed by the integral of 1/(z − a) over the closed chain is zero for each point 'a' not in the region. This means that the closed chain does not wind around points outside the region. Then Cauchy's theorem can be stated as the integral of a function holomorphic in an open set taken around any cycle in the open set is zero. An example is furnished by the ring shaped region. This version is crucial for rigorous derivation of Laurent series
and Cauchy's residue formula without involving any physical notions such as cross cuts or deformations. The version enables to extend Cauchy's theorem to multiply connected regions analytically.
for these functions, and from that deduce these functions are in fact infinitely differentiable.
The condition that U be simply connected means that U has no "holes" or, in homotopy
terms, that the fundamental group
of U is trivial; for instance, every open disk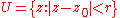 qualifies. The condition is crucial; consider
qualifies. The condition is crucial; consider
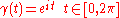
which traces out the unit circle, and then the path integral
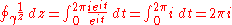
is non-zero; the Cauchy integral theorem does not apply here since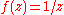 is not defined (and certainly not holomorphic) at
is not defined (and certainly not holomorphic) at  .
.
One important consequence of the theorem is that path integrals of holomorphic functions on simply connected domains can be computed in a
manner familiar from the fundamental theorem of real calculus
: let U be a simply connected open subset of C, let f : U → C be a holomorphic function, and let γ be a piecewise continuously differentiable path in U with start point a and end point b. If F is a complex antiderivative of f, then
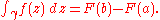
The Cauchy integral theorem is valid in slightly stronger forms than given above. e.g. Let U be a simply connected open subset of C and f a function which is holomorphic on U and continuous on
. Let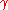 be a loop in
be a loop in  which is uniform limit of a sequence
which is uniform limit of a sequence 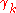 of rectifiable loops in U with bounded length. Then, applying the Cauchy theorem to the
of rectifiable loops in U with bounded length. Then, applying the Cauchy theorem to the 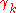 , and passing to the limit one has
, and passing to the limit one has
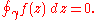
See e.g. for a more general result.
The Cauchy integral theorem leads to Cauchy's integral formula
and the residue theorem
.
and the fact that the real and imaginary parts of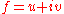 must satisfy the Cauchy–Riemann equations in the region bounded by
must satisfy the Cauchy–Riemann equations in the region bounded by 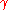 , and moreover in the open neighborhood U of this region.
, and moreover in the open neighborhood U of this region.
We can break the integrand , as well as the differential
, as well as the differential  into their real and imaginary components:
into their real and imaginary components:
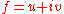

In this case we have
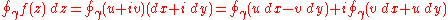
By Green's theorem, we may then replace the integrals around the closed contour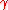 with an area integral throughout the domain
with an area integral throughout the domain  that is enclosed by
that is enclosed by 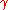 as follows:
as follows:
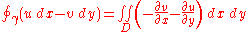
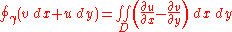
However, being the real and imaginary parts of a function analytic in the domain ,
,  and
and  must satisfy the Cauchy–Riemann equations there:
must satisfy the Cauchy–Riemann equations there:
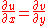
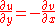
We therefore find that both integrands (and hence their integrals) are zero
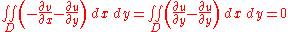
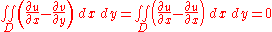
This gives the desired result
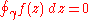
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Cauchy integral theorem (also known as the Cauchy–Goursat theorem) in complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, named after Augustin-Louis Cauchy, is an important statement about line integral
Line integral
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...
s for holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s in the complex plane
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
. Essentially, it says that if two different paths connect the same two points, and a function is holomorphic everywhere "in between" the two paths, then the two path integrals of the function will be the same.
The theorem is usually formulated for closed paths as follows: let U be an open subset of C which is simply connected, let f : U → C be a holomorphic function, and let
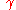 be a rectifiable path in U whose start point is equal to its end point. Then
be a rectifiable path in U whose start point is equal to its end point. Then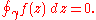
A precise (homology
Homology (mathematics)
In mathematics , homology is a certain general procedure to associate a sequence of abelian groups or modules with a given mathematical object such as a topological space or a group...
) version can be stated using winding number
Winding number
In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...
s. The winding number of a closed curve around a point 'a' not on the curve is the integral of 1/(2 i)f(z), where f(z) = 1/(z − a) around the curve. It is an integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
.
Briefly, the path integral along a Jordan curve of a function holomorphic in the interior of the curve, is zero. Instead of a single closed path we can consider a linear combination of closed path where the scalars are integers. Such a combination is called a closed chain and one defines integral along the chain as the linear combination of integrals over individual paths. A closed chain is called a cycle in a region if it is homologous to zero in the region, that is the winding number, expressed by the integral of 1/(z − a) over the closed chain is zero for each point 'a' not in the region. This means that the closed chain does not wind around points outside the region. Then Cauchy's theorem can be stated as the integral of a function holomorphic in an open set taken around any cycle in the open set is zero. An example is furnished by the ring shaped region. This version is crucial for rigorous derivation of Laurent series
Laurent series
In mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...
and Cauchy's residue formula without involving any physical notions such as cross cuts or deformations. The version enables to extend Cauchy's theorem to multiply connected regions analytically.
Discussion
As was shown by Goursat, Cauchy's integral theorem can be proven assuming only that the complex derivative f '(z) exists everywhere in U. This is significant, because one can then prove Cauchy's integral formulaCauchy's integral formula
In mathematics, Cauchy's integral formula, named after Augustin-Louis Cauchy, is a central statement in complex analysis. It expresses the fact that a holomorphic function defined on a disk is completely determined by its values on the boundary of the disk, and it provides integral formulas for all...
for these functions, and from that deduce these functions are in fact infinitely differentiable.
The condition that U be simply connected means that U has no "holes" or, in homotopy
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
terms, that the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of U is trivial; for instance, every open disk
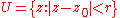 qualifies. The condition is crucial; consider
qualifies. The condition is crucial; consider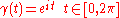
which traces out the unit circle, and then the path integral
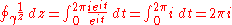
is non-zero; the Cauchy integral theorem does not apply here since
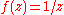 is not defined (and certainly not holomorphic) at
is not defined (and certainly not holomorphic) at  .
.One important consequence of the theorem is that path integrals of holomorphic functions on simply connected domains can be computed in a
manner familiar from the fundamental theorem of real calculus
Fundamental theorem of calculus
The first part of the theorem, sometimes called the first fundamental theorem of calculus, shows that an indefinite integration can be reversed by a differentiation...
: let U be a simply connected open subset of C, let f : U → C be a holomorphic function, and let γ be a piecewise continuously differentiable path in U with start point a and end point b. If F is a complex antiderivative of f, then
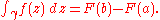
The Cauchy integral theorem is valid in slightly stronger forms than given above. e.g. Let U be a simply connected open subset of C and f a function which is holomorphic on U and continuous on

Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
. Let
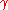 be a loop in
be a loop in  which is uniform limit of a sequence
which is uniform limit of a sequence 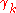 of rectifiable loops in U with bounded length. Then, applying the Cauchy theorem to the
of rectifiable loops in U with bounded length. Then, applying the Cauchy theorem to the 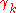 , and passing to the limit one has
, and passing to the limit one has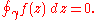
See e.g. for a more general result.
The Cauchy integral theorem leads to Cauchy's integral formula
Cauchy's integral formula
In mathematics, Cauchy's integral formula, named after Augustin-Louis Cauchy, is a central statement in complex analysis. It expresses the fact that a holomorphic function defined on a disk is completely determined by its values on the boundary of the disk, and it provides integral formulas for all...
and the residue theorem
Residue theorem
The residue theorem, sometimes called Cauchy's Residue Theorem, in complex analysis is a powerful tool to evaluate line integrals of analytic functions over closed curves and can often be used to compute real integrals as well. It generalizes the Cauchy integral theorem and Cauchy's integral formula...
.
Proof
If one assumes that the partial derivatives of a holomorphic function are continuous, the Cauchy integral theorem can be proved as a direct consequence of Green's theoremGreen's theorem
In mathematics, Green's theorem gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C...
and the fact that the real and imaginary parts of
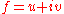 must satisfy the Cauchy–Riemann equations in the region bounded by
must satisfy the Cauchy–Riemann equations in the region bounded by 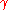 , and moreover in the open neighborhood U of this region.
, and moreover in the open neighborhood U of this region.We can break the integrand
 , as well as the differential
, as well as the differential  into their real and imaginary components:
into their real and imaginary components: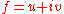

In this case we have
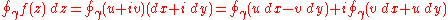
By Green's theorem, we may then replace the integrals around the closed contour
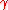 with an area integral throughout the domain
with an area integral throughout the domain  that is enclosed by
that is enclosed by 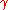 as follows:
as follows: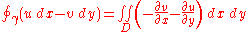
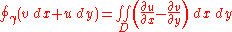
However, being the real and imaginary parts of a function analytic in the domain
 ,
,  and
and  must satisfy the Cauchy–Riemann equations there:
must satisfy the Cauchy–Riemann equations there: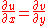
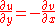
We therefore find that both integrands (and hence their integrals) are zero
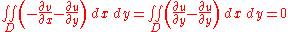
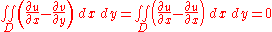
This gives the desired result
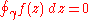
See also
- Cauchy–Riemann equations
- Morera's theoremMorera's theoremIn complex analysis, a branch of mathematics, Morera's theorem, named after Giacinto Morera, gives an important criterion for proving that a function is holomorphic....
- Methods of contour integrationMethods of contour integrationIn the mathematical field of complex analysis, contour integration is a method of evaluating certain integrals along paths in the complex plane.Contour integration is closely related to the calculus of residues, a methodology of complex analysis....
- Residue (complex analysis)Residue (complex analysis)In mathematics, more specifically complex analysis, the residue is a complex number proportional to the contour integral of a meromorphic function along a path enclosing one of its singularities...
External links
- The site Anil's maths computer notes contains a simple treatment of the global (homology version of Cauchy's Theorem assuming Cauchy's theorem for a triangle and a convex region offering simplified Dixon's proof and deduces Cauchy's theorem for a simply connected region

