
Bogoliubov transformation
Encyclopedia
In theoretical physics
, the Bogoliubov transformation, named after Nikolay Bogolyubov
, is a unitary transformation
from a unitary representation
of some canonical commutation relation algebra or canonical anticommutation relation algebra into another unitary representation, induced by an isomorphism
of the commutation relation algebra. The Bogoliubov transformation is often used to diagonalize Hamiltonian
s, which yields the steady-state solutions of the corresponding Schrödinger equation
. The solutions of BCS theory
in a homogeneous system, for example, are found using a Bogoliubov transformation. The Bogoliubov transformation is also important for understanding the Unruh effect
, Hawking radiation
and many other topics.
for bosonic creation and annihilation operators
in the harmonic basis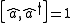
Define a new pair of operators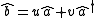
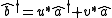
where the latter is the hermitian conjugate of the first. The Bogoliubov transformation is a canonical transformation of these operators. To find the conditions on the constants u and v such that the transformation remains canonical, the commutator is expanded, viz.
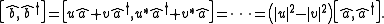
It can be seen that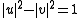 is the condition for which the transformation is canonical. Since the form of this condition is reminiscent of the hyperbolic identity
is the condition for which the transformation is canonical. Since the form of this condition is reminiscent of the hyperbolic identity
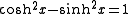 , the constants u and v can be parametrized as
, the constants u and v can be parametrized as
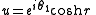
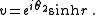
relation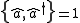 ,
,
the same transformation with u and v becomes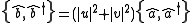
To make the transformation canonical, u and v can be parameterized as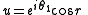

under consideration is equipped with these operators, and henceforth describes a higher-dimensional quantum harmonic oscillator
(usually an infinite-dimensional one).
The ground state
of the corresponding Hamiltonian
is annihilated by all the annihilation operators:

All excited states are obtained as linear combination
s of the ground state excited by some creation operators:
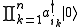
One may redefine the creation and the annihilation operators by a linear redefinition:
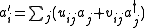
where the coefficients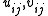 must satisfy certain rules to guarantee that the annihilation operators and the creation operators
must satisfy certain rules to guarantee that the annihilation operators and the creation operators 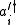 , defined by the Hermitian conjugate equation, have the same commutator
, defined by the Hermitian conjugate equation, have the same commutator
s.
The equation above defines the Bogoliubov transformation of the operators.
The ground state annihilated by all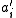 is different from the original ground state
is different from the original ground state  and they can be viewed as the Bogoliubov transformations of one another using the operator-state correspondence. They can also be defined as squeezed coherent states.
and they can be viewed as the Bogoliubov transformations of one another using the operator-state correspondence. They can also be defined as squeezed coherent states.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, the Bogoliubov transformation, named after Nikolay Bogolyubov
Nikolay Bogolyubov
Nikolay Nikolaevich Bogolyubov was a Russian and Ukrainian Soviet mathematician and theoretical physicist known for a significant contribution to quantum field theory, classical and quantum statistical mechanics, and to the theory of dynamical systems; a recipient of the Dirac Prize...
, is a unitary transformation
Unitary transformation
In mathematics, a unitary transformation may be informally defined as a transformation that respects the inner product: the inner product of two vectors before the transformation is equal to their inner product after the transformation....
from a unitary representation
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
of some canonical commutation relation algebra or canonical anticommutation relation algebra into another unitary representation, induced by an isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
of the commutation relation algebra. The Bogoliubov transformation is often used to diagonalize Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
s, which yields the steady-state solutions of the corresponding Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
. The solutions of BCS theory
BCS theory
BCS theory — proposed by Bardeen, Cooper, and Schrieffer in 1957 — is the first microscopic theory of superconductivity since its discovery in 1911. The theory describes superconductivity as a microscopic effect caused by a "condensation" of pairs of electrons into a boson-like state...
in a homogeneous system, for example, are found using a Bogoliubov transformation. The Bogoliubov transformation is also important for understanding the Unruh effect
Unruh effect
The Unruh effect , was first described by Stephen Fulling in 1973, Paul Davies in 1975 and Bill Unruh in 1976. It is the prediction that an accelerating observer will observe black-body radiation where an inertial observer would observe none...
, Hawking radiation
Hawking radiation
Hawking radiation is a thermal radiation with a black body spectrum predicted to be emitted by black holes due to quantum effects. It is named after the physicist Stephen Hawking, who provided a theoretical argument for its existence in 1974, and sometimes also after the physicist Jacob Bekenstein...
and many other topics.
Single bosonic mode example
Consider the canonical commutation relationCommutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
for bosonic creation and annihilation operators
Creation and annihilation operators
Creation and annihilation operators are mathematical operators that have widespread applications in quantum mechanics, notably in the study of quantum harmonic oscillators and many-particle systems. An annihilation operator lowers the number of particles in a given state by one...
in the harmonic basis
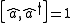
Define a new pair of operators
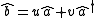
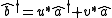
where the latter is the hermitian conjugate of the first. The Bogoliubov transformation is a canonical transformation of these operators. To find the conditions on the constants u and v such that the transformation remains canonical, the commutator is expanded, viz.
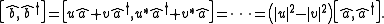
It can be seen that
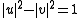 is the condition for which the transformation is canonical. Since the form of this condition is reminiscent of the hyperbolic identity
is the condition for which the transformation is canonical. Since the form of this condition is reminiscent of the hyperbolic identityHyperbolic function
In mathematics, hyperbolic functions are analogs of the ordinary trigonometric, or circular, functions. The basic hyperbolic functions are the hyperbolic sine "sinh" , and the hyperbolic cosine "cosh" , from which are derived the hyperbolic tangent "tanh" and so on.Just as the points form a...
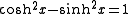 , the constants u and v can be parametrized as
, the constants u and v can be parametrized as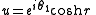
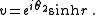
Fermionic mode
For the anticommutationCommutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
relation
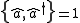 ,
,the same transformation with u and v becomes
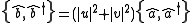
To make the transformation canonical, u and v can be parameterized as
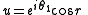

Multimode example
The Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
under consideration is equipped with these operators, and henceforth describes a higher-dimensional quantum harmonic oscillator
Quantum harmonic oscillator
The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics...
(usually an infinite-dimensional one).
The ground state
Ground state
The ground state of a quantum mechanical system is its lowest-energy state; the energy of the ground state is known as the zero-point energy of the system. An excited state is any state with energy greater than the ground state...
of the corresponding Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
is annihilated by all the annihilation operators:

All excited states are obtained as linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
s of the ground state excited by some creation operators:
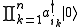
One may redefine the creation and the annihilation operators by a linear redefinition:
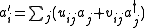
where the coefficients
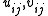 must satisfy certain rules to guarantee that the annihilation operators and the creation operators
must satisfy certain rules to guarantee that the annihilation operators and the creation operators 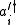 , defined by the Hermitian conjugate equation, have the same commutator
, defined by the Hermitian conjugate equation, have the same commutatorCommutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
s.
The equation above defines the Bogoliubov transformation of the operators.
The ground state annihilated by all
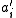 is different from the original ground state
is different from the original ground state  and they can be viewed as the Bogoliubov transformations of one another using the operator-state correspondence. They can also be defined as squeezed coherent states.
and they can be viewed as the Bogoliubov transformations of one another using the operator-state correspondence. They can also be defined as squeezed coherent states.

