
Gas in a harmonic trap
Encyclopedia
The results of the quantum harmonic oscillator
can be used to look at the equilibrium situation for a quantum ideal gas in a harmonic trap, which is a harmonic potential containing a large number of particles that do not interact with each other except for instantaneous thermalizing collisions. This situation is of great practical importance since many experimental studies of Bose gas
es are conducted in such harmonic traps.
Using the results from either Maxwell-Boltzmann statistics, Bose-Einstein statistics or Fermi-Dirac statistics
we use the
Thomas-Fermi approximation and go to the limit of a very large trap, and express the degeneracy of the energy states ( ) as a differential, and summations over states as integrals. We will then be in a position to calculate the thermodynamic properties of the gas using the partition function
) as a differential, and summations over states as integrals. We will then be in a position to calculate the thermodynamic properties of the gas using the partition function
or the grand partition function. Only the case of massive particles will be considered, although the results can be extended to massless particles as well, much as was done in the case of the ideal gas in a box
. More complete calculations will be left to separate articles, but some simple examples will be given in this article.
 . The energy of a particular state is given by:
. The energy of a particular state is given by:
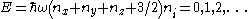
Suppose each set of quantum numbers specify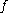 states where
states where 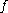 is the number of internal degrees of freedom of the particle that can be altered by collision. For example, a spin-1/2 particle would have
is the number of internal degrees of freedom of the particle that can be altered by collision. For example, a spin-1/2 particle would have 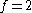 , one for each spin state. We can think of each possible state of a particle as a point on a 3-dimensional grid of positive integers. The Thomas-Fermi approximation assumes that the quantum numbers are so large that they may be considered to be a continuum. For large values of
, one for each spin state. We can think of each possible state of a particle as a point on a 3-dimensional grid of positive integers. The Thomas-Fermi approximation assumes that the quantum numbers are so large that they may be considered to be a continuum. For large values of  , we can estimate the number of states with energy less than or equal to
, we can estimate the number of states with energy less than or equal to 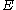 from the above equation as:
from the above equation as:
which is just times the volume of the tetrahedron formed by the plane described by the energy equation and the bounding planes of the positive octant. The number of states with energy between
times the volume of the tetrahedron formed by the plane described by the energy equation and the bounding planes of the positive octant. The number of states with energy between  and
and  is therefore:
is therefore:
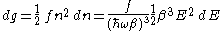
Notice that in using this continuum approximation, we have lost the ability to characterize the low-energy states, including the ground state where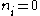 . For most cases this will not be a problem, but when considering Bose-Einstein
. For most cases this will not be a problem, but when considering Bose-Einstein
condensation, in which a large portion of the gas is in or near the ground state, we will need to recover the ability to deal with low energy states.
Without using the continuum approximation, the number of particles with energy is given by:
is given by:

where
with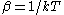 , with
, with 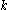 being Boltzmann's constant,
being Boltzmann's constant,  being temperature
being temperature
, and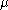 being the chemical potential
being the chemical potential
. Using the continuum approximation, the number of particles with energy between
with energy between  and
and 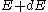 is now written:
is now written:
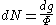
 is
is  and is equal to the fraction of particles which have values for
and is equal to the fraction of particles which have values for 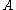 between
between 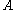 and
and  :
:
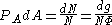
It follows that:

Using these relationships we obtain the energy distribution function:

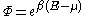
Integrating the energy distribution function and solving for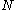 gives:
gives:
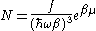
Substituting into the original energy distribution function gives:

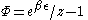
where is defined as:
is defined as:

Integrating the energy distribution function and solving for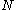 gives:
gives:
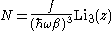
Where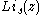 is the polylogarithm function. The polylogarithm term must always be positive and real, which means its value will go from 0 to
is the polylogarithm function. The polylogarithm term must always be positive and real, which means its value will go from 0 to 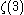 as
as  goes from 0 to 1. As the temperature goes to zero,
goes from 0 to 1. As the temperature goes to zero, 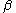 will become larger and larger, until finally
will become larger and larger, until finally 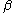 will reach a critical value
will reach a critical value 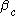 , where
, where 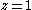 and
and
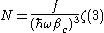
The temperature at which is the critical temperature at which a Bose-Einstein condensate begins to form. The problem is, as mentioned above, the ground state has been ignored in the continuum approximation. It turns out that the above expression expresses the number of bosons in excited states rather well, and so we may write:
is the critical temperature at which a Bose-Einstein condensate begins to form. The problem is, as mentioned above, the ground state has been ignored in the continuum approximation. It turns out that the above expression expresses the number of bosons in excited states rather well, and so we may write:
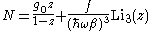
where the added term is the number of particles in the ground state. (The ground state energy has been ignored.) This equation will hold down to zero temperature. Further results can be found in the article on the ideal Bose gas
.

Integrating the energy distribution function gives:

where again,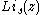 is the polylogarithm function. Further results can be found in the article on the ideal Fermi gas
is the polylogarithm function. Further results can be found in the article on the ideal Fermi gas
.
Quantum harmonic oscillator
The quantum harmonic oscillator is the quantum-mechanical analog of the classical harmonic oscillator. Because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point, it is one of the most important model systems in quantum mechanics...
can be used to look at the equilibrium situation for a quantum ideal gas in a harmonic trap, which is a harmonic potential containing a large number of particles that do not interact with each other except for instantaneous thermalizing collisions. This situation is of great practical importance since many experimental studies of Bose gas
Bose gas
An ideal Bose gas is a quantum-mechanical version of a classical ideal gas. It is composed of bosons, which have an integer value of spin, and obey Bose–Einstein statistics...
es are conducted in such harmonic traps.
Using the results from either Maxwell-Boltzmann statistics, Bose-Einstein statistics or Fermi-Dirac statistics
Fermi-Dirac statistics
Fermi–Dirac statistics is a part of the science of physics that describes the energies of single particles in a system comprising many identical particles that obey the Pauli Exclusion Principle...
we use the
Thomas-Fermi approximation and go to the limit of a very large trap, and express the degeneracy of the energy states (
 ) as a differential, and summations over states as integrals. We will then be in a position to calculate the thermodynamic properties of the gas using the partition function
) as a differential, and summations over states as integrals. We will then be in a position to calculate the thermodynamic properties of the gas using the partition functionPartition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
or the grand partition function. Only the case of massive particles will be considered, although the results can be extended to massless particles as well, much as was done in the case of the ideal gas in a box
Gas in a box
In quantum mechanics, the results of the quantum particle in a box can be used to look at the equilibrium situation for a quantum ideal gas in a box which is a box containing a large number of molecules which do not interact with each other except for instantaneous thermalizing collisions...
. More complete calculations will be left to separate articles, but some simple examples will be given in this article.
Thomas Fermi approximation for the degeneracy of states
For massive particles in a harmonic well, the states of the particle are enumerated by a set of quantum numbers . The energy of a particular state is given by:
. The energy of a particular state is given by: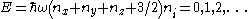
Suppose each set of quantum numbers specify
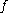 states where
states where 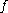 is the number of internal degrees of freedom of the particle that can be altered by collision. For example, a spin-1/2 particle would have
is the number of internal degrees of freedom of the particle that can be altered by collision. For example, a spin-1/2 particle would have 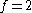 , one for each spin state. We can think of each possible state of a particle as a point on a 3-dimensional grid of positive integers. The Thomas-Fermi approximation assumes that the quantum numbers are so large that they may be considered to be a continuum. For large values of
, one for each spin state. We can think of each possible state of a particle as a point on a 3-dimensional grid of positive integers. The Thomas-Fermi approximation assumes that the quantum numbers are so large that they may be considered to be a continuum. For large values of  , we can estimate the number of states with energy less than or equal to
, we can estimate the number of states with energy less than or equal to 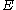 from the above equation as:
from the above equation as: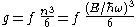
which is just
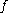 times the volume of the tetrahedron formed by the plane described by the energy equation and the bounding planes of the positive octant. The number of states with energy between
times the volume of the tetrahedron formed by the plane described by the energy equation and the bounding planes of the positive octant. The number of states with energy between 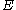 and
and  is therefore:
is therefore: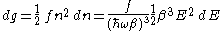
Notice that in using this continuum approximation, we have lost the ability to characterize the low-energy states, including the ground state where
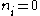 . For most cases this will not be a problem, but when considering Bose-Einstein
. For most cases this will not be a problem, but when considering Bose-Einsteincondensation, in which a large portion of the gas is in or near the ground state, we will need to recover the ability to deal with low energy states.
Without using the continuum approximation, the number of particles with energy
 is given by:
is given by:
where
 |
for particles obeying Maxwell-Boltzmann statistics |
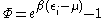 |
for particles obeying Bose-Einstein statistics |
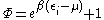 |
for particles obeying Fermi-Dirac statistics Fermi-Dirac statistics Fermi–Dirac statistics is a part of the science of physics that describes the energies of single particles in a system comprising many identical particles that obey the Pauli Exclusion Principle... |
with
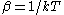 , with
, with 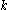 being Boltzmann's constant,
being Boltzmann's constant,  being temperature
being temperatureTemperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
, and
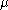 being the chemical potential
being the chemical potentialChemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
. Using the continuum approximation, the number of particles
 with energy between
with energy between  and
and 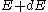 is now written:
is now written: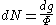
The energy distribution function
We are now in a position to determine some distribution functions for the "gas in a harmonic trap." The distribution function for any variable is
is  and is equal to the fraction of particles which have values for
and is equal to the fraction of particles which have values for 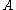 between
between 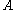 and
and  :
: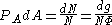
It follows that:

Using these relationships we obtain the energy distribution function:

Massive Maxwell-Boltzmann particles
For this case: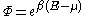
Integrating the energy distribution function and solving for
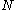 gives:
gives: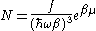
Substituting into the original energy distribution function gives:

Massive Bose-Einstein particles
For this case: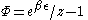
where
 is defined as:
is defined as:
Integrating the energy distribution function and solving for
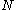 gives:
gives: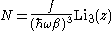
Where
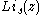 is the polylogarithm function. The polylogarithm term must always be positive and real, which means its value will go from 0 to
is the polylogarithm function. The polylogarithm term must always be positive and real, which means its value will go from 0 to 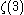 as
as  goes from 0 to 1. As the temperature goes to zero,
goes from 0 to 1. As the temperature goes to zero, 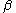 will become larger and larger, until finally
will become larger and larger, until finally 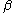 will reach a critical value
will reach a critical value 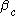 , where
, where 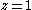 and
and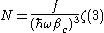
The temperature at which
 is the critical temperature at which a Bose-Einstein condensate begins to form. The problem is, as mentioned above, the ground state has been ignored in the continuum approximation. It turns out that the above expression expresses the number of bosons in excited states rather well, and so we may write:
is the critical temperature at which a Bose-Einstein condensate begins to form. The problem is, as mentioned above, the ground state has been ignored in the continuum approximation. It turns out that the above expression expresses the number of bosons in excited states rather well, and so we may write: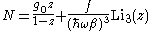
where the added term is the number of particles in the ground state. (The ground state energy has been ignored.) This equation will hold down to zero temperature. Further results can be found in the article on the ideal Bose gas
Bose gas
An ideal Bose gas is a quantum-mechanical version of a classical ideal gas. It is composed of bosons, which have an integer value of spin, and obey Bose–Einstein statistics...
.
Massive Fermi-Dirac particles (e.g. electrons in a metal)
For this case:
Integrating the energy distribution function gives:

where again,
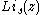 is the polylogarithm function. Further results can be found in the article on the ideal Fermi gas
is the polylogarithm function. Further results can be found in the article on the ideal Fermi gasFermi gas
A Fermi gas is an ensemble of a large number of fermions. Fermions, named after Enrico Fermi, are particles that obey Fermi–Dirac statistics. These statistics determine the energy distribution of fermions in a Fermi gas in thermal equilibrium, and is characterized by their number density,...
.

