Bootstrapping populations
Encyclopedia
Starting with a sample 
observed from a random variable
X having a given distribution law
with a set of non fixed parameters which we denote with a vector
, a parametric inference
problem consists of computing suitable values – call them estimates
– of these parameters precisely on the basis of the sample. An estimate is suitable if replacing it with the unknown parameter does not cause major damage in next computations. In Algorithmic inference
, suitability of an estimate reads in terms of compatibility with the observed sample.
In this framework, resampling methods
are aimed at generating a set of candidate values to replace the unknown parameters that we read as compatible replicas of them. They represent a population of specifications of a random vector
compatible with an observed sample, where the compatibility of its values has the properties of a probability distribution. By plugging parameters into the expression of the questioned distribution law, we bootstrap entire populations of random variables compatible with the observed sample.
The rationale of the algorithms computing the replicas, which we denote population bootstrap procedures, is to identify a set of statistics
exhibiting specific properties, denoting a well behavior
, w.r.t. the unknown parameters. The statistics are expressed as functions of the observed values
, by definition. The 
may be expressed as a function of the unknown parameters and a random seed specification 
through the sampling mechanism 
, in turn. Then, by plugging the second expression in the former, we obtain 
expressions as functions of seeds and parameters – the master equations – that we invert to find values of the latter as a function of: i) the statistics, whose values in turn are fixed at the observed ones; and ii) the seeds, which are random according to their own distribution. Hence from a set of seed samples we obtain a set of parameter replicas.
of a random variable X and a sampling mechanism 
for X, we have 
, with 
. Focusing on well-behaved statistic
s,
for their parameters, the master equations read
For each sample seed
you obtain a vector of parameters 
from the solution of the above system with 
fixed to the observed values.
Having computed a huge set of compatible vectors, say N, you obtain the empirical marginal distribution of
by:
denoting by
the j-th component of the generic solution of (1) and by 
the indicator function of 
in the interval 
.
Some indeterminacies remain with X discrete which we will consider shortly.
The whole procedure may be summed up in the form of the following Algorithm, where the index
of 
denotes the parameters vector which the statics vector refers to.
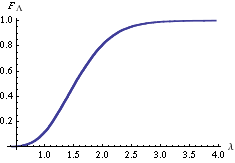
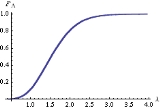
You may easily see from a table of sufficient statistics that we obtain the curve in the picture on the left by computing the empirical distribution (2) on the population obtained through the above algorithm when: i) X is an Exponential random variable, ii) 
, and
,
and the curve in the picture on the right when: i) X is a Uniform random variable in
, ii) 
, and
.
populations compatible with a sample is obtained is not a function of the sample size. Instead, it is a function of the number of seeds we draw. In turn, this number is purely a matter of computational time but does not require any extension of the observed data. With other bootstrapping methods
focusing on a generation of sample replicas (like those proposed by ) the accuracy of the estimate distributions depends on the sample size.
expected to represent a Pareto distribution, whose specification requires values for the parameters 
and k , we have that the cumulative distribution function reads:
.
A sampling mechanism
has 
uniform seed
U and explaining function
described by:
A relevant statistic
is constituted by the pair of joint sufficient statistics
for
and K, respectively 
.
The master equations read
with
.
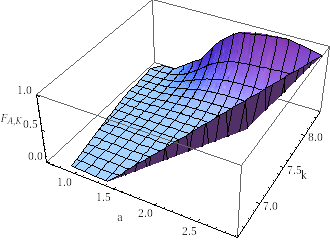
Figure on the right reports the three dimensional plot of the empirical cumulative distribution function (2) of
.
observed from a random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
X having a given distribution law
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
with a set of non fixed parameters which we denote with a vector
, a parametric inferenceParametric statistics
Parametric statistics is a branch of statistics that assumes that the data has come from a type of probability distribution and makes inferences about the parameters of the distribution. Most well-known elementary statistical methods are parametric....
problem consists of computing suitable values – call them estimates
Estimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
– of these parameters precisely on the basis of the sample. An estimate is suitable if replacing it with the unknown parameter does not cause major damage in next computations. In Algorithmic inference
Algorithmic inference
Algorithmic inference gathers new developments in the statistical inference methods made feasible by the powerful computing devices widely available to any data analyst...
, suitability of an estimate reads in terms of compatibility with the observed sample.
In this framework, resampling methods
Resampling (statistics)
In statistics, resampling is any of a variety of methods for doing one of the following:# Estimating the precision of sample statistics by using subsets of available data or drawing randomly with replacement from a set of data points # Exchanging labels on data points when performing significance...
are aimed at generating a set of candidate values to replace the unknown parameters that we read as compatible replicas of them. They represent a population of specifications of a random vector
compatible with an observed sample, where the compatibility of its values has the properties of a probability distribution. By plugging parameters into the expression of the questioned distribution law, we bootstrap entire populations of random variables compatible with the observed sample.The rationale of the algorithms computing the replicas, which we denote population bootstrap procedures, is to identify a set of statistics
exhibiting specific properties, denoting a well behaviorWell-behaved statistic
A well-behaved statistic is a term sometimes used in the theory of statistics to describe part of a procedure. This usage is broadly similar to the use of well-behaved in more general mathematics...
, w.r.t. the unknown parameters. The statistics are expressed as functions of the observed values
, by definition. The may be expressed as a function of the unknown parameters and a random seed specification through the sampling mechanism , in turn. Then, by plugging the second expression in the former, we obtain expressions as functions of seeds and parameters – the master equations – that we invert to find values of the latter as a function of: i) the statistics, whose values in turn are fixed at the observed ones; and ii) the seeds, which are random according to their own distribution. Hence from a set of seed samples we obtain a set of parameter replicas.Method
Given a of a random variable X and a sampling mechanism for X, we have , with . Focusing on well-behaved statisticWell-behaved statistic
A well-behaved statistic is a term sometimes used in the theory of statistics to describe part of a procedure. This usage is broadly similar to the use of well-behaved in more general mathematics...
s,
 |
 |
 |
for their parameters, the master equations read
 |
|
 |
(1) |
 |
For each sample seed
you obtain a vector of parameters from the solution of the above system with fixed to the observed values.Having computed a huge set of compatible vectors, say N, you obtain the empirical marginal distribution of
by:  |
(2) |
denoting by
the j-th component of the generic solution of (1) and by the indicator function of in the interval .Some indeterminacies remain with X discrete which we will consider shortly.
The whole procedure may be summed up in the form of the following Algorithm, where the index
of denotes the parameters vector which the statics vector refers to.Algorithm
| Generating parameter populations through a bootstrap |
|---|
Given a sample  from a random variable with parameter vector  unknown,
|
for 
;
of 
from the sample;
of size m from the seed random variable;
as a solution of (1) in θ with 
and 
;
to 
; population., and,and the curve in the picture on the right when: i) X is a Uniform random variable in
, ii) , and.Remark
Note that the accuracy with which a parameter distribution law ofpopulations compatible with a sample is obtained is not a function of the sample size. Instead, it is a function of the number of seeds we draw. In turn, this number is purely a matter of computational time but does not require any extension of the observed data. With other bootstrapping methods
Bootstrapping (statistics)
In statistics, bootstrapping is a computer-based method for assigning measures of accuracy to sample estimates . This technique allows estimation of the sample distribution of almost any statistic using only very simple methods...
focusing on a generation of sample replicas (like those proposed by ) the accuracy of the estimate distributions depends on the sample size.
Example
For expected to represent a Pareto distribution, whose specification requires values for the parameters and k , we have that the cumulative distribution function reads:.A sampling mechanism
has uniform seedUniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
U and explaining function
described by:A relevant statistic
is constituted by the pair of joint sufficient statisticsSufficiency (statistics)
In statistics, a sufficient statistic is a statistic which has the property of sufficiency with respect to a statistical model and its associated unknown parameter, meaning that "no other statistic which can be calculated from the same sample provides any additional information as to the value of...
for
and K, respectively .The master equations read
with
.Figure on the right reports the three dimensional plot of the empirical cumulative distribution function (2) of
.