Birkhoff's representation theorem
Encyclopedia
In mathematics
, Birkhoff's representation theorem for distributive lattices states that the elements of any finite distributive lattice
can be represented as finite sets, in such a way that the lattice operations correspond to unions
and intersections
of sets. The theorem can be interpreted as providing a one-to-one correspondence
between distributive lattices and partial orders, between quasi-ordinal knowledge spaces
and preorder
s, or between finite topological space
s and preorders. It is named after Garrett Birkhoff
, who published a proof of it in 1937.
The name “Birkhoff's representation theorem” has also been applied to two other results of Birkhoff, one from 1935 on the representation of Boolean algebras as families of sets closed under union, intersection, and complement (so-called fields of sets, closely related to the rings of sets used by Birkhoff to represent distributive lattices), and Birkhoff's HSP theorem representing algebras as products of irreducible algebras. Birkhoff's representation theorem has also been called the fundamental theorem for finite distributive lattices.
has a lattice of sets as its family of open sets. Because set unions and intersections obey the distributive law, any lattice defined in this way is a distributive lattice. Birkhoff's theorem states that in fact all finite distributive lattices can be obtained this way, and later generalizations of Birkhoff's theorem state the same thing for infinite lattices.
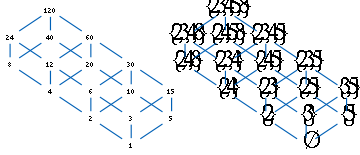 Consider the divisor
Consider the divisor
s of some composite number, such as (in the figure) 120, partially ordered by divisibility. Any two divisors of 120, such as 12 and 20, have a unique greatest common factor
12 ∧ 20 = 4, the largest number that divides both of them, and a unique least common multiple
12 ∨ 20 = 60; both of these numbers are also divisors of 120. These two operations ∨ and ∧ satisfy the distributive law, in either of two equivalent forms: (x ∧ y) ∨ z = (x ∨ z) ∧ (y ∨ z) and (x ∨ y) ∧ z = (x ∧ z) ∨ (y ∧ z), for all x, y, and z. Therefore, the divisors form a finite distributive lattice
.
One may associate each divisor with the set of prime power
s that divide it: thus, 12 is associated with the set {2,3,4}, while 20 is associated with the set {2,4,5}. Then 12 ∧ 20 = 4 is associated with the set {2,3,4} ∩ {2,4,5} = {2,4}, while 12 ∨ 20 = 60 is associated with the set {2,3,4} ∪ {2,4,5} = {2,3,4,5}, so the join and meet operations of the lattice correspond to union and intersection of sets.
The prime powers 2, 3, 4, 5, and 8 appearing as elements in these sets may themselves be partially ordered by divisibility; in this smaller partial order, 2 ≤ 4 ≤ 8 and there are no order relations between other pairs. The 16 sets that are associated with divisors of 120 are the lower sets of this smaller partial order, subsets of elements such that if x ≤ y and y belongs to the subset, then x must also belong to the subset. From any lower set L, one can recover the associated divisor by computing the least common multiple of the prime powers in L. Thus, the partial order on the five prime powers 2, 3, 4, 5, and 8 carries enough information to recover the entire original 16-element divisibility lattice.
Birkhoff's theorem states that this relation between the operations ∧ and ∨ of the lattice of divisors and the operations ∩ and ∪ of the associated sets of prime powers is not coincidental, and not dependent on the specific properties of prime numbers and divisibility: the elements of any finite distributive lattice may be associated with lower sets of a partial order in the same way.
As another example, the application of Birkhoff's theorem to the family of subset
s of an n-element set, partially ordered by inclusion, produces the free distributive lattice with n generators. The number of elements in this lattice is given by the Dedekind number
s.
In any lattice, a join-prime element must be join-irreducible. Equivalently, an element that is not join-irreducible is not join-prime. For, if an element x is not join-irreducible, there exist smaller y and z such that x = y ∨ z. But then x ≤ y ∨ z, and x is not less than or equal to either y or z, showing that it is not join-prime.
There exist lattices in which the join-prime elements form a proper subset of the join-irreducible elements, but in a distributive lattice the two types of elements coincide. For, suppose that x is join-irreducible, and that x ≤ y ∨ z. This inequality is equivalent to the statement that x = x ∧ (y ∨ z), and by the distributive law x = (x ∧ y) ∨ (x ∧ z). But since x is join-irreducible, at least one of the two terms in this join must be x itself, showing that either x = x ∧ y (equivalently x ≤ y) or x = x ∧ z (equivalently x ≤ z).
The lattice ordering on the subset of join-irreducible elements forms a partial order; Birkhoff's theorem states that the lattice itself can be recovered from the lower sets of this partial order.
That is, there is a one-to-one order-preserving correspondence between elements of L and lower sets of the partial order. The lower set corresponding to an element x of L is simply the set of join-irreducible elements of L that are less than or equal to x, and the element of L corresponding to a lower set S of join-irreducible elements is the join of S.
If one starts with a lower set S, lets x be the join of S, and constructs lower set T of the join-irreducible elements less than or equal to x, then S = T. For, every element of S clearly belongs to T, and any join-irreducible element less than or equal to x must (by join-primality) be less than or equal to one of the members of S, and therefore must (by the assumption that S is a lower set) belong to S itself. Conversely, if one starts with an element x of L, lets S be the join-irreducible elements less than or equal to x, and constructs y as the join of S, then x = y. For, as a join of elements less than or equal to x, y can be no greater than x itself, but if x is join-irreducible then x belongs to S while if x is the join of two or more join-irreducible items then they must again belong to S, so y ≥ x. Therefore, the correspondence is one-to-one and the theorem is proved.
that is closed
under the operations of set unions and set intersections; later, motivated by applications in mathematical psychology
, called the same structure a quasi-ordinal knowledge space
. If the sets in a ring of sets are ordered by inclusion, they form a distributive lattice. The elements of the sets may be given a preorder
in which x ≤ y whenever some set in the ring contains x but not y. The ring of sets itself is then the family of lower sets of this preorder, and any preorder gives rise to a ring of sets in this way.
Let 2 denote the partial order on the two-element set {0, 1}, with the order relation 0 < 1, and (following Stanley) let J(P) denote the distributive lattice of lower sets of a finite partial order P. Then the elements of J(P) correspond one-for-one to the order-preserving functions from P to 2. For, if ƒ is such a function, ƒ−1(0) forms a lower set, and conversely if L is a lower set one may define an order-preserving function ƒL that maps L to 0 and that maps the remaining elements of P to 1. If g is any order-preserving function from Q to P, one may define a function g* from J(P) to J(Q) that uses the composition of functions to map any element L of J(P) to ƒL ∘ g. This composite function maps Q to 2 and therefore corresponds to an element g*(L) = (ƒL ∘ g)−1(0) of J(Q). Further, for any x and y in J(P), g*(x ∧ y) = g*(x) ∧ g*(y) (an element of Q is mapped by g to the lower set x ∩ y if and only if belongs both to the set of elements mapped to x and the set of elements mapped to y) and symmetrically g*(x ∨ y) = g*(x) ∨ g*(y). Additionally, the bottom element of J(P) (the function that maps all elements of P to 0) is mapped by g* to the bottom element of J(Q), and the top element of J(P) is mapped by g* to the top element of J(Q). That is, g* is a homomorphism of bounded lattices.
However, the elements of P themselves correspond one-for-one with bounded lattice homomorphisms from J(P) to 2. For, if x is any element of P, one may define a bounded lattice homomorphism jx that maps all lower sets containing x to 1 and all other lower sets to 0. And, for any lattice homomorphism from J(P) to 2, the elements of J(P) that are mapped to 1 must have a unique minimal element x (the meet of all elements mapped to 1), which must be join-irreducible (it cannot be the join of any set of elements mapped to 0), so every lattice homomorphism has the form jx for some x. Again, from any bounded lattice homomorphism h from J(P) to J(Q) one may use composition of functions to define an order-preserving map h* from Q to P. It may be verified that g** = g for any order-preserving map g from Q to P and that and h** = h for any bounded lattice homomorphism h from J(P) to J(Q).
In category theoretic
terminology, J is a contravariant hom-functor J = Hom(—,2) that defines a duality of categories
between, on the one hand, the category of finite partial orders and order-preserving maps, and on the other hand the category of finite distributive lattices and bounded lattice homomorphisms.
s that do not divide x. However, elements in infinite distributive lattices may still be represented as sets via Stone's representation theorem for distributive lattices, a form of Stone duality
in which each lattice element corresponds to a compact
open set
in a certain topological space
. This generalized representation theorem can be expressed as a category-theoretic
duality
between distributive lattices and coherent space
s (sometimes called spectral space
s), topological spaces in which the compact open sets are closed under intersection and form a base
for the topology. Hilary Priestley showed that Stone's representation theorem could be interpreted as an extension of the idea of representing lattice elements by lower sets of a partial order, using Nachbin's idea of ordered topological spaces. Stone spaces with an additional partial order linked with the topology via Priestley separation axiom
can also be used to represent bounded distributive lattices. Such spaces are known as Priestley space
s. Further, certain bitopological space
s, namely pairwise Stone space
s, generalize Stone's original approach by utilizing two topologies on a set to represent an abstract distributve lattice. Thus, Birkhoff's representation theorem extends to the case of infinite (bounded) distributive lattices in at least three different ways, summed up in duality theory for distributive lattices
.
Birkhoff's representation theorem may also be generalized to finite structures other than distributive lattices. In a distributive lattice, the self-dual median operation
gives rise to a median algebra
, and the covering relation of the lattice forms a median graph
. Finite median algebras and median graphs have a dual structure
as the set of solutions of a 2-satisfiability
instance; formulate this structure equivalently as the family of initial stable sets
in a mixed graph. For a distributive lattice, the corresponding mixed graph has no undirected edges, and the initial stable sets are just the lower sets of the transitive closure
of the graph. Equivalently, for a distributive lattice, the implication graph
of the 2-satisfiability instance can be partitioned into two connected components
, one on the positive variables of the instance and the other on the negative variables; the transitive closure of the positive component is the underlying partial order of the distributive lattice.
Another result analogous to Birkhoff's representation theorem, but applying to a broader class of lattices, is the theorem of that any finite join-distributive lattice may be represented as an antimatroid
, a family of sets closed under unions but in which closure under intersections has been replaced by the property that each nonempty set has a removable element.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Birkhoff's representation theorem for distributive lattices states that the elements of any finite distributive lattice
Distributive lattice
In mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...
can be represented as finite sets, in such a way that the lattice operations correspond to unions
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
and intersections
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of sets. The theorem can be interpreted as providing a one-to-one correspondence
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
between distributive lattices and partial orders, between quasi-ordinal knowledge spaces
Knowledge space
In mathematical psychology, a knowledge space is a combinatorial structure describing the possible states of knowledge of a human learner.To form a knowledge space, one models a domain of knowledge as a set of concepts, and a feasible state of knowledge as a subset of that set containing the...
and preorder
Preorder
In mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders...
s, or between finite topological space
Finite topological space
In mathematics, a finite topological space is a topological space for which the underlying point set is finite. That is, it is a topological space for which there are only finitely many points....
s and preorders. It is named after Garrett Birkhoff
Garrett Birkhoff
Garrett Birkhoff was an American mathematician. He is best known for his work in lattice theory.The mathematician George Birkhoff was his father....
, who published a proof of it in 1937.
The name “Birkhoff's representation theorem” has also been applied to two other results of Birkhoff, one from 1935 on the representation of Boolean algebras as families of sets closed under union, intersection, and complement (so-called fields of sets, closely related to the rings of sets used by Birkhoff to represent distributive lattices), and Birkhoff's HSP theorem representing algebras as products of irreducible algebras. Birkhoff's representation theorem has also been called the fundamental theorem for finite distributive lattices.
Understanding the theorem
Many lattices can be defined in such a way that the elements of the lattice are represented by sets, the join operation of the lattice is represented by set union, and the meet operation of the lattice is represented by set intersection. For instance, the Boolean lattice defined from the family of all subsets of a finite set has this property. More generally any finite topological spaceFinite topological space
In mathematics, a finite topological space is a topological space for which the underlying point set is finite. That is, it is a topological space for which there are only finitely many points....
has a lattice of sets as its family of open sets. Because set unions and intersections obey the distributive law, any lattice defined in this way is a distributive lattice. Birkhoff's theorem states that in fact all finite distributive lattices can be obtained this way, and later generalizations of Birkhoff's theorem state the same thing for infinite lattices.
Examples
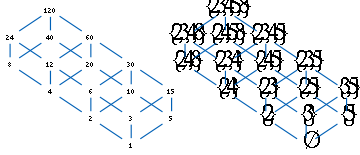
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
s of some composite number, such as (in the figure) 120, partially ordered by divisibility. Any two divisors of 120, such as 12 and 20, have a unique greatest common factor
Greatest common divisor
In mathematics, the greatest common divisor , also known as the greatest common factor , or highest common factor , of two or more non-zero integers, is the largest positive integer that divides the numbers without a remainder.For example, the GCD of 8 and 12 is 4.This notion can be extended to...
12 ∧ 20 = 4, the largest number that divides both of them, and a unique least common multiple
Least common multiple
In arithmetic and number theory, the least common multiple of two integers a and b, usually denoted by LCM, is the smallest positive integer that is a multiple of both a and b...
12 ∨ 20 = 60; both of these numbers are also divisors of 120. These two operations ∨ and ∧ satisfy the distributive law, in either of two equivalent forms: (x ∧ y) ∨ z = (x ∨ z) ∧ (y ∨ z) and (x ∨ y) ∧ z = (x ∧ z) ∨ (y ∧ z), for all x, y, and z. Therefore, the divisors form a finite distributive lattice
Distributive lattice
In mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...
.
One may associate each divisor with the set of prime power
Prime power
In mathematics, a prime power is a positive integer power of a prime number.For example: 5=51, 9=32 and 16=24 are prime powers, while6=2×3, 15=3×5 and 36=62=22×32 are not...
s that divide it: thus, 12 is associated with the set {2,3,4}, while 20 is associated with the set {2,4,5}. Then 12 ∧ 20 = 4 is associated with the set {2,3,4} ∩ {2,4,5} = {2,4}, while 12 ∨ 20 = 60 is associated with the set {2,3,4} ∪ {2,4,5} = {2,3,4,5}, so the join and meet operations of the lattice correspond to union and intersection of sets.
The prime powers 2, 3, 4, 5, and 8 appearing as elements in these sets may themselves be partially ordered by divisibility; in this smaller partial order, 2 ≤ 4 ≤ 8 and there are no order relations between other pairs. The 16 sets that are associated with divisors of 120 are the lower sets of this smaller partial order, subsets of elements such that if x ≤ y and y belongs to the subset, then x must also belong to the subset. From any lower set L, one can recover the associated divisor by computing the least common multiple of the prime powers in L. Thus, the partial order on the five prime powers 2, 3, 4, 5, and 8 carries enough information to recover the entire original 16-element divisibility lattice.
Birkhoff's theorem states that this relation between the operations ∧ and ∨ of the lattice of divisors and the operations ∩ and ∪ of the associated sets of prime powers is not coincidental, and not dependent on the specific properties of prime numbers and divisibility: the elements of any finite distributive lattice may be associated with lower sets of a partial order in the same way.
As another example, the application of Birkhoff's theorem to the family of subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of an n-element set, partially ordered by inclusion, produces the free distributive lattice with n generators. The number of elements in this lattice is given by the Dedekind number
Dedekind number
Image:Monotone Boolean functions 0,1,2,3.svg|400px|thumb|right| The free distributive lattices of monotonic Boolean functions on 0, 1, 2, and 3 arguments, with 2, 3, 6, and 20 elements respectively...
s.
The partial order of join-irreducibles
In a lattice, an element x is join-irreducible if x is not the join of a finite set of other elements. Equivalently, x is join-irreducible if it is neither the bottom element of the lattice (the join of zero elements) nor the join of any two smaller elements. For instance, in the lattice of divisors of 120, there is no pair of elements whose join is 4, so 4 is join-irreducible. An element x is join-prime if, whenever x ≤ y ∨ z, either x ≤ y or x ≤ z. In the same lattice, 4 is join-prime: whenever lcm(y,z) is divisible by 4, at least one of y and z must itself be divisible by 4.In any lattice, a join-prime element must be join-irreducible. Equivalently, an element that is not join-irreducible is not join-prime. For, if an element x is not join-irreducible, there exist smaller y and z such that x = y ∨ z. But then x ≤ y ∨ z, and x is not less than or equal to either y or z, showing that it is not join-prime.
There exist lattices in which the join-prime elements form a proper subset of the join-irreducible elements, but in a distributive lattice the two types of elements coincide. For, suppose that x is join-irreducible, and that x ≤ y ∨ z. This inequality is equivalent to the statement that x = x ∧ (y ∨ z), and by the distributive law x = (x ∧ y) ∨ (x ∧ z). But since x is join-irreducible, at least one of the two terms in this join must be x itself, showing that either x = x ∧ y (equivalently x ≤ y) or x = x ∧ z (equivalently x ≤ z).
The lattice ordering on the subset of join-irreducible elements forms a partial order; Birkhoff's theorem states that the lattice itself can be recovered from the lower sets of this partial order.
Birkhoff's theorem
In any partial order, the lower sets form a lattice in which the lattice's partial ordering is given by set inclusion, the join operation corresponds to set union, and the meet operation corresponds to set intersection, because unions and intersections preserve the property of being a lower set. Because set unions and intersections obey the distributive law, this is a distributive lattice. Birkhoff's theorem states that any finite distributive lattice can be constructed in this way.- Theorem. Any finite distributive lattice L is isomorphic to the lattice of lower sets of the partial order of the join-irreducible elements of L.
That is, there is a one-to-one order-preserving correspondence between elements of L and lower sets of the partial order. The lower set corresponding to an element x of L is simply the set of join-irreducible elements of L that are less than or equal to x, and the element of L corresponding to a lower set S of join-irreducible elements is the join of S.
If one starts with a lower set S, lets x be the join of S, and constructs lower set T of the join-irreducible elements less than or equal to x, then S = T. For, every element of S clearly belongs to T, and any join-irreducible element less than or equal to x must (by join-primality) be less than or equal to one of the members of S, and therefore must (by the assumption that S is a lower set) belong to S itself. Conversely, if one starts with an element x of L, lets S be the join-irreducible elements less than or equal to x, and constructs y as the join of S, then x = y. For, as a join of elements less than or equal to x, y can be no greater than x itself, but if x is join-irreducible then x belongs to S while if x is the join of two or more join-irreducible items then they must again belong to S, so y ≥ x. Therefore, the correspondence is one-to-one and the theorem is proved.
Rings of sets and preorders
defined a ring of sets to be a family of setsFamily of sets
In set theory and related branches of mathematics, a collection F of subsets of a given set S is called a family of subsets of S, or a family of sets over S. More generally, a collection of any sets whatsoever is called a family of sets...
that is closed
Closure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
under the operations of set unions and set intersections; later, motivated by applications in mathematical psychology
Mathematical psychology
Mathematical psychology is an approach to psychological research that is based on mathematical modeling of perceptual, cognitive and motor processes, and on the establishment of law-like rules that relate quantifiable stimulus characteristics with quantifiable behavior...
, called the same structure a quasi-ordinal knowledge space
Knowledge space
In mathematical psychology, a knowledge space is a combinatorial structure describing the possible states of knowledge of a human learner.To form a knowledge space, one models a domain of knowledge as a set of concepts, and a feasible state of knowledge as a subset of that set containing the...
. If the sets in a ring of sets are ordered by inclusion, they form a distributive lattice. The elements of the sets may be given a preorder
Preorder
In mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders...
in which x ≤ y whenever some set in the ring contains x but not y. The ring of sets itself is then the family of lower sets of this preorder, and any preorder gives rise to a ring of sets in this way.
Functoriality
Birkhoff's theorem, as stated above, is a correspondence between individual partial orders and distributive lattices. However, it can also be extended to a correspondence between order-preserving functions of partial orders and bounded homomorphisms of the corresponding distributive lattices. The direction of these maps is reversed in this correspondence.Let 2 denote the partial order on the two-element set {0, 1}, with the order relation 0 < 1, and (following Stanley) let J(P) denote the distributive lattice of lower sets of a finite partial order P. Then the elements of J(P) correspond one-for-one to the order-preserving functions from P to 2. For, if ƒ is such a function, ƒ−1(0) forms a lower set, and conversely if L is a lower set one may define an order-preserving function ƒL that maps L to 0 and that maps the remaining elements of P to 1. If g is any order-preserving function from Q to P, one may define a function g* from J(P) to J(Q) that uses the composition of functions to map any element L of J(P) to ƒL ∘ g. This composite function maps Q to 2 and therefore corresponds to an element g*(L) = (ƒL ∘ g)−1(0) of J(Q). Further, for any x and y in J(P), g*(x ∧ y) = g*(x) ∧ g*(y) (an element of Q is mapped by g to the lower set x ∩ y if and only if belongs both to the set of elements mapped to x and the set of elements mapped to y) and symmetrically g*(x ∨ y) = g*(x) ∨ g*(y). Additionally, the bottom element of J(P) (the function that maps all elements of P to 0) is mapped by g* to the bottom element of J(Q), and the top element of J(P) is mapped by g* to the top element of J(Q). That is, g* is a homomorphism of bounded lattices.
However, the elements of P themselves correspond one-for-one with bounded lattice homomorphisms from J(P) to 2. For, if x is any element of P, one may define a bounded lattice homomorphism jx that maps all lower sets containing x to 1 and all other lower sets to 0. And, for any lattice homomorphism from J(P) to 2, the elements of J(P) that are mapped to 1 must have a unique minimal element x (the meet of all elements mapped to 1), which must be join-irreducible (it cannot be the join of any set of elements mapped to 0), so every lattice homomorphism has the form jx for some x. Again, from any bounded lattice homomorphism h from J(P) to J(Q) one may use composition of functions to define an order-preserving map h* from Q to P. It may be verified that g** = g for any order-preserving map g from Q to P and that and h** = h for any bounded lattice homomorphism h from J(P) to J(Q).
In category theoretic
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
terminology, J is a contravariant hom-functor J = Hom(—,2) that defines a duality of categories
Equivalence of categories
In category theory, an abstract branch of mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics...
between, on the one hand, the category of finite partial orders and order-preserving maps, and on the other hand the category of finite distributive lattices and bounded lattice homomorphisms.
Generalizations
In an infinite distributive lattice, it may not be the case that the lower sets of the join-irreducible elements are in one-to-one correspondence with lattice elements. Indeed, there may be no join-irreducibles at all. This happens, for instance, in the lattice of all integers, ordered with the reverse of the usual divisibility ordering (so x ≤ y when y divides x): any number x can be expressed as the join of numbers xp and xq where p and q are distinct prime numberPrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s that do not divide x. However, elements in infinite distributive lattices may still be represented as sets via Stone's representation theorem for distributive lattices, a form of Stone duality
Stone duality
In mathematics, there is an ample supply of categorical dualities between certain categories of topological spaces and categories of partially ordered sets. Today, these dualities are usually collected under the label Stone duality, since they form a natural generalization of Stone's representation...
in which each lattice element corresponds to a compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
in a certain topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
. This generalized representation theorem can be expressed as a category-theoretic
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
duality
Equivalence of categories
In category theory, an abstract branch of mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics...
between distributive lattices and coherent space
Coherent space
In proof theory, a coherent space is a concept introduced in the semantic study of linear logic.Let a set C be given. Two subsets S,T ⊆ C are said to be orthogonal, written S ⊥ T, if S ∩ T is ∅ or a singleton...
s (sometimes called spectral space
Spectral space
In mathematics, a spectral space is a topological space which is homeomorphic to the spectrum of a commutative ring.-Definition:Let X be a topological space and let K\circ be the set of allquasi-compact and open subsets of X...
s), topological spaces in which the compact open sets are closed under intersection and form a base
Base (topology)
In mathematics, a base B for a topological space X with topology T is a collection of open sets in T such that every open set in T can be written as a union of elements of B. We say that the base generates the topology T...
for the topology. Hilary Priestley showed that Stone's representation theorem could be interpreted as an extension of the idea of representing lattice elements by lower sets of a partial order, using Nachbin's idea of ordered topological spaces. Stone spaces with an additional partial order linked with the topology via Priestley separation axiom
Priestley space
In mathematics, a Priestley space is an ordered topological space with special properties. Priestley spaces are named after Hilary Priestley who introduced and investigated them. Priestley spaces play a fundamental role in the study of distributive lattices...
can also be used to represent bounded distributive lattices. Such spaces are known as Priestley space
Priestley space
In mathematics, a Priestley space is an ordered topological space with special properties. Priestley spaces are named after Hilary Priestley who introduced and investigated them. Priestley spaces play a fundamental role in the study of distributive lattices...
s. Further, certain bitopological space
Bitopological space
In mathematics, a bitopological space is a set endowed with two topologies. Typically, if the set is X and the topologies are \sigma and \tau then we refer to the bitopological space as .-Bi-continuity:...
s, namely pairwise Stone space
Pairwise Stone space
In mathematics and particularly in topology, pairwise Stone space is a bitopological space \scriptstyle which is pairwise compact, pairwise Hausdorff, and pairwise zero-dimensional....
s, generalize Stone's original approach by utilizing two topologies on a set to represent an abstract distributve lattice. Thus, Birkhoff's representation theorem extends to the case of infinite (bounded) distributive lattices in at least three different ways, summed up in duality theory for distributive lattices
Duality theory for distributive lattices
In mathematics, duality theory for distributive lattices provides three different representations of bounded distributive lattices via Priestley spaces, spectral spaces, and pairwise Stone spaces...
.
Birkhoff's representation theorem may also be generalized to finite structures other than distributive lattices. In a distributive lattice, the self-dual median operation

gives rise to a median algebra
Median algebra
In mathematics, a median algebra is a set with a ternary operation < x,y,z > satisfying a set of axioms which generalise the notion of median or majority function, as a Boolean function.The axioms are# < x,y,y > = y...
, and the covering relation of the lattice forms a median graph
Median graph
In mathematics, and more specifically graph theory, a median graph is an undirected graph in which any three vertices a, b, and c have a unique median: a vertex m that belongs to shortest paths between any two of a, b, and c.The concept of median graphs has long been studied, for instance by or ...
. Finite median algebras and median graphs have a dual structure
as the set of solutions of a 2-satisfiability
2-satisfiability
In computer science, 2-satisfiability is the problem of determining whether a collection of two-valued variables with constraints on pairs of variables can be assigned values satisfying all the constraints...
instance; formulate this structure equivalently as the family of initial stable sets
Independent set
In graph theory, an independent set or stable set is a set of vertices in a graph, no two of which are adjacent. That is, it is a set I of vertices such that for every two vertices in I, there is no edge connecting the two. Equivalently, each edge in the graph has at most one endpoint in I...
in a mixed graph. For a distributive lattice, the corresponding mixed graph has no undirected edges, and the initial stable sets are just the lower sets of the transitive closure
Transitive closure
In mathematics, the transitive closure of a binary relation R on a set X is the transitive relation R+ on set X such that R+ contains R and R+ is minimal . If the binary relation itself is transitive, then the transitive closure will be that same binary relation; otherwise, the transitive closure...
of the graph. Equivalently, for a distributive lattice, the implication graph
Implication graph
In mathematical logic, an implication graph is a skew-symmetric directed graph G composed of vertex set V and directed edge set E. Each vertex in V represents the truth status of a Boolean literal, and each directed edge from vertex u to vertex v represents the material implication "If the literal...
of the 2-satisfiability instance can be partitioned into two connected components
Connected component (graph theory)
In graph theory, a connected component of an undirected graph is a subgraph in which any two vertices are connected to each other by paths, and which is connected to no additional vertices. For example, the graph shown in the illustration on the right has three connected components...
, one on the positive variables of the instance and the other on the negative variables; the transitive closure of the positive component is the underlying partial order of the distributive lattice.
Another result analogous to Birkhoff's representation theorem, but applying to a broader class of lattices, is the theorem of that any finite join-distributive lattice may be represented as an antimatroid
Antimatroid
In mathematics, an antimatroid is a formal system that describes processes in which a set is built up by including elements one at a time, and in which an element, once available for inclusion, remains available until it is included...
, a family of sets closed under unions but in which closure under intersections has been replaced by the property that each nonempty set has a removable element.

