Bicycle performance
Encyclopedia
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
a person must expend to travel a given distance, investigators have calculated it to be the most efficient self-powered means of transportation
Mode of transport
Mode of transport is a term used to distinguish substantially different ways to perform transport. The most dominant modes of transport are aviation, land transport, which includes rail, road and off-road transport, and ship transport...
. From a mechanical viewpoint, up to 99% of the energy delivered by the rider into the pedals
Bicycle pedal
A bicycle pedal is the part of a bicycle that the rider pushes with their foot to propel the bicycle. It provides the connection between the cyclist's foot or shoe and the crank allowing the leg to turn the bottom bracket spindle and propel the bicycle's wheels...
is transmitted to the wheels
Bicycle wheel
A bicycle wheel is a wheel, most commonly a wire wheel, designed for bicycle. A pair is often called a wheelset, especially in the context of ready built "off the shelf" performance-oriented wheels....
, although the use of gearing mechanisms
Bicycle gearing
A bicycle gear or gear ratio refers to the rate at which the rider's legs turn compared to the rate at which the wheels turn. Bicycle gearing refers to how the gear ratio is set or changed. On some bicycles, there is only one gear so the ratio is fixed. Most modern bicycles have multiple gears,...
may reduce this by 10–15%. In terms of the ratio of cargo
Cargo
Cargo is goods or produce transported, generally for commercial gain, by ship, aircraft, train, van or truck. In modern times, containers are used in most intermodal long-haul cargo transport.-Marine:...
weight a bicycle can carry to total weight, it is also a most efficient means of cargo transportation.
Energy efficiency
A human being traveling on a bicycleBicycle
A bicycle, also known as a bike, pushbike or cycle, is a human-powered, pedal-driven, single-track vehicle, having two wheels attached to a frame, one behind the other. A person who rides a bicycle is called a cyclist, or bicyclist....
at low to medium speeds of around 10–15 mph (16–24 km/h), using only the power required to walk, is the most energy-efficient means of transport generally available. Air drag, which increases roughly with the square of speed, requires increasingly higher power
Power (physics)
In physics, power is the rate at which energy is transferred, used, or transformed. For example, the rate at which a light bulb transforms electrical energy into heat and light is measured in watts—the more wattage, the more power, or equivalently the more electrical energy is used per unit...
outputs relative to speed, power increasing with the cube of speed as power equals force times velocity. A bicycle in which the rider lies in a supine position
Supine position
The supine position is a position of the body: lying down with the face up, as opposed to the prone position, which is face down, sometimes with the hands behind the head or neck. When used in surgical procedures, it allows access to the peritoneal, thoracic and pericardial regions; as well as the...
is referred to as a recumbent bicycle
Recumbent bicycle
A recumbent bicycle is a bicycle that places the rider in a laid-back reclining position. Most recumbent riders choose this type of design for ergonomic reasons; the rider's weight is distributed comfortably over a larger area, supported by back and buttocks...
or, if covered in an aerodynamic fairing to achieve very low air drag, as a streamliner
Streamliner
A streamliner is a vehicle incorporating streamlining in a shape providing reduced air resistance. The term is applied to high-speed railway trainsets of the 1930s to 1950s, and to their successor "bullet trains". Less commonly, the term is applied to fully faired recumbent bicycles...
.
Watt
The watt is a derived unit of power in the International System of Units , named after the Scottish engineer James Watt . The unit, defined as one joule per second, measures the rate of energy conversion.-Definition:...
s to walk at 5 km/h. That same person on a bicycle, on the same ground, with the same power output, can average 15 km/h, so energy expenditure in terms of kcal
Calorie
The calorie is a pre-SI metric unit of energy. It was first defined by Nicolas Clément in 1824 as a unit of heat, entering French and English dictionaries between 1841 and 1867. In most fields its use is archaic, having been replaced by the SI unit of energy, the joule...
/(kg·km) is roughly one-third as much. Generally used figures are
- 1.62 kJJouleThe joule ; symbol J) is a derived unit of energy or work in the International System of Units. It is equal to the energy expended in applying a force of one newton through a distance of one metre , or in passing an electric current of one ampere through a resistance of one ohm for one second...
/(km∙kg) or 0.28 kcal/(mi∙lb) for cycling, - 3.78 kJ/(km∙kg) or 0.653 kcal/(mi∙lb) for walking/running,
- 16.96 kJ/(km∙kg) or 2.93 kcal/(mi∙lb) for swimming.
Amateur bicycle racers can typically produce 3 watt
Watt
The watt is a derived unit of power in the International System of Units , named after the Scottish engineer James Watt . The unit, defined as one joule per second, measures the rate of energy conversion.-Definition:...
s/kg for more than an hour (e.g., around 210 watts for a 70 kg rider), with top amateurs producing 5 W/kg and elite athletes achieving 6 W/kg for similar lengths of time. Elite track sprinters
Sprint (cycling)
The sprint or match sprint is a track cycling event involving between 2 and 4 riders, though they are usually run as a one-on-one match race between opponents who, unlike in the individual pursuit, start next to each other.- Racing style :...
are able to attain an instantaneous maximum output of around 2,000 watts, or in excess of 25 W/kg; elite road cyclists may produce 1,600 to 1,700 watts as an instantaneous maximum in their burst to the finish line at the end of a five-hour long road race. Even at moderate speeds, most power is spent in overcoming the aerodynamic drag
Drag (physics)
In fluid dynamics, drag refers to forces which act on a solid object in the direction of the relative fluid flow velocity...
force, which increases with the square of speed. Thus, the power required to overcome drag increases with the cube of the speed.
Typical speeds
Typical speeds for bicycles are 15 to 30 km/h (10 to 20 mph). On a fast racing bicycleRacing bicycle
A racing bicycle, also known as a road bike, is a bicycle designed for competitive road cycling, a sport governed by according to the rules of the Union Cycliste Internationale...
, a reasonably fit rider can ride at 50 km/h (30 mph) on flat ground for short periods. The highest speed officially
recorded for any human-powered vehicle (HPV) on level ground and with calm winds and without external aids (such as motor pacing and wind-blocks) is 133.284 km/h (82.819 mph). That record was set in 2009 by Sam Whittingham
Sam Whittingham
Sam Whittingham is a Canadian cyclist who has held several world records on recumbent bicycles., he holds the following world records under the sanction of the International Human Powered Vehicle Association:...
in the Varna. In the 1989 Race Across America
Race Across America
The Race Across America, or RAAM, is an ultra marathon bicycle race across the United States that started in 1982 as the Great American Bike Race....
, a group of HPV's crossed the United States in just 6 days. The highest speed officially recorded for a bicycle ridden in a conventional upright position under fully faired conditions was 82.52 km/h (51.29 mph) over 200m. That record was set in 1986 by Jim Glover on a Moulton AM7 at the 3rd international HPV scientific symposium at Vancouver.
Weight vs power
There has been major corporate competition to lower the weight of racing bikes through the use of advanced materials and components. Additionally, advanced wheelsBicycle wheel
A bicycle wheel is a wheel, most commonly a wire wheel, designed for bicycle. A pair is often called a wheelset, especially in the context of ready built "off the shelf" performance-oriented wheels....
are available with low-friction
Friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...
bearings
Bearing (mechanical)
A bearing is a device to allow constrained relative motion between two or more parts, typically rotation or linear movement. Bearings may be classified broadly according to the motions they allow and according to their principle of operation as well as by the directions of applied loads they can...
and other features to lower resistance, however in measured tests these components have almost no effect on cycling performance when riding on flat ground. For instance, lowering a bike's weight by 1 lb (0.45359237 kg), a major effort considering it may weigh less than 15 lb (6.8 kg) to start with, will have the same effect over a 40 km time trial
Time trial
In many racing sports an athlete will compete in a time trial against the clock to secure the fastest time. In cycling, for example, a time trial can be a single track cycling event, or an individual or team time trial on the road, and either or both of the latter may form components of...
on flat ground as removing a protrusion into the air the size of a pencil. Also, the UCI
UCI
UCI usually refers to the Union Cycliste Internationale, the world governing body for the sport of cycling.UCI may also refer to:* United Cinemas International* United Kennel Clubs International...
sets a limit on the minimum weight of bicycles to be used in sanctioned races, to discourage making structures so thin that they become unsafe. For these reasons recent designs have concentrated on lowering wind resistance by using aerodynamically shaped tubing, flat spoke
Spoke
A spoke is one of some number of rods radiating from the center of a wheel , connecting the hub with the round traction surface....
s on the wheels, and handlebars
Bicycle handlebar
Bicycle handlebar or often bicycle handlebars refers to the steering mechanism for bicycles; the equivalent of a steering wheel. Besides steering, handlebars also often support a portion of the rider's weight, depending on their riding position, and provide a convenient mounting place for brake...
that position the rider's torso and arms for minimal drag. These changes can impact performance dramatically, cutting minutes off a time trial. Less weight results in larger time savings on uphill terrain.
Kinetic energy of a rotating wheel
Consider the kinetic energyKinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
and "rotating mass" of a bicycle
Bicycle
A bicycle, also known as a bike, pushbike or cycle, is a human-powered, pedal-driven, single-track vehicle, having two wheels attached to a frame, one behind the other. A person who rides a bicycle is called a cyclist, or bicyclist....
in order to examine the energy impacts of rotating versus non-rotating mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
.
The translational kinetic energy of an object in motion
Motion (physics)
In physics, motion is a change in position of an object with respect to time. Change in action is the result of an unbalanced force. Motion is typically described in terms of velocity, acceleration, displacement and time . An object's velocity cannot change unless it is acted upon by a force, as...
is:
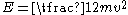,Where
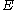is energy in jouleJoule
The joule ; symbol J) is a derived unit of energy or work in the International System of Units. It is equal to the energy expended in applying a force of one newton through a distance of one metre , or in passing an electric current of one ampere through a resistance of one ohm for one second...
s,
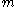is mass in kg, and 
is velocityVelocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
in meters per second. For a rotating mass (such as a wheel), the rotational kinetic energy is given by
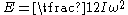,where
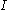is the moment of inertiaMoment of inertia
In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
,
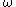(pronunciation: omega) is the angular velocityAngular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
in radians per second. For a wheel with all its mass at the outer edge (a fair approximation for a bicycle wheel), the moment of inertia is
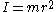.Where
is the radius in metersThe angular velocity is related to the translational velocity and the radius of the tire. As long as there is no slipping,
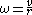.When a rotating mass is moving down the road, its total kinetic energy is the sum of its translational kinetic energy and its rotational kinetic energy:
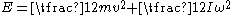
Substituting for
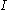and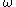 
, we get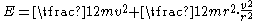
The
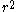terms cancel, and we finally get
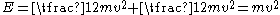.In other words, a mass on the tire has twice the kinetic energy of a
non-rotating mass on the bike. There is a kernel of truth in the old saying
that "A pound off the wheels = 2 pounds off the frame."
This all depends, of course, on how well a thin hoop approximates the bicycle wheel. In reality, all the mass cannot be at the radius. For comparison, the opposite extreme might be a disk wheel where the mass is distributed evenly throughout the interior. In this case
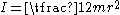and so the resulting total kinetic energy becomes 
. A pound off the disk wheels = only 1.5 pounds off the frame. Most real bicycle wheels will be somewhere between these two extremes.One other interesting point from this equation is that for a bicycle wheel
Bicycle wheel
A bicycle wheel is a wheel, most commonly a wire wheel, designed for bicycle. A pair is often called a wheelset, especially in the context of ready built "off the shelf" performance-oriented wheels....
that is not slipping, the kinetic energy is independent of wheel radius. In
other words, the advantage of 650C or other smaller wheels is due to their
lower weight (less material in a smaller circumference
Circumference
The circumference is the distance around a closed curve. Circumference is a special perimeter.-Circumference of a circle:The circumference of a circle is the length around it....
) rather than their
smaller diameter
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
, as is often stated. The KE for other rotating masses on
the bike is tiny compared to that of the wheels. For example, pedals turn at
about
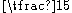the speed of wheels, so their KE is about
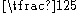(per unit weight) that of a spinning wheel. As their center of mass turns on a smaller radius, this is further reduced.Convert to kilocalories
Assuming that a rotating wheel can be treated as the mass of rim and tireTire
A tire or tyre is a ring-shaped covering that fits around a wheel rim to protect it and enable better vehicle performance by providing a flexible cushion that absorbs shock while keeping the wheel in close contact with the ground...
and 2/3 of the mass of the spokes, all at the center of the rim/tire. For a 180 lb (82 kg) rider on an 18 lb (8 kg) bike (90 kg total) at 25 mph (40 km/h ; 11.2 m/s), the KE is 5625 joules for the bike/rider plus 94 joules for a rotating wheel (combined 1.5 kg of rims/tires/spokes). Converting joules to kilocalories (multiply by 0.0002389) gives 1.4 kilocalories (large calories, nutritional calories, or Calories with a capital "C").
That 1.4 kilocalories is the energy necessary to accelerate from a standstill, or the heat to be dissipated
Dissipation
In physics, dissipation embodies the concept of a dynamical system where important mechanical models, such as waves or oscillations, lose energy over time, typically from friction or turbulence. The lost energy converts into heat, which raises the temperature of the system. Such systems are called...
by the brakes to stop the bike. These are kilocalories, so 1.4 kilocalories will heat 1 kg of water 1.4 degrees Celsius. Since aluminum's heat capacity
Heat capacity
Heat capacity , or thermal capacity, is the measurable physical quantity that characterizes the amount of heat required to change a substance's temperature by a given amount...
is 21% of water, this amount of energy would heat 800 g of alloy rims 8 °C (15 °F) in a rapid stop. Rims do not get very hot from stopping on flat ground. To get the rider's energy expenditure, consider the 24% efficiency factor to get 5.8 kilocalories—accelerating a bike/rider to 25 mph (40 km/h) requires about 0.5% of the energy required to ride at 25 mph (40 km/h) for an hour. This energy expenditure would take place in about 15 seconds, at a rate of roughly 0.4 kilocalories per second, while steady state
Steady state
A system in a steady state has numerous properties that are unchanging in time. This implies that for any property p of the system, the partial derivative with respect to time is zero:...
riding at 25 mph (40 km/h) requires 0.3 kilocalories per second.
Advantages of light wheels
The advantage of light bikes, and particularly light wheels, from a KE standpoint is that KE only comes into play when speed changes, and there are certainly two cases where lighter wheels should have an advantage: sprintsSprint (cycling)
The sprint or match sprint is a track cycling event involving between 2 and 4 riders, though they are usually run as a one-on-one match race between opponents who, unlike in the individual pursuit, start next to each other.- Racing style :...
, and corner jumps in a criterium
Criterium
A criterium, or crit, is a bike race held on a short course , often run on closed-off city center streets....
.
In a 250 m sprint from 36 to 47 km/h to (22 to 29 mph), a 90 kg bike/rider with 1.75 kg of rims/tires/spokes increases KE by 6,360 joule
Joule
The joule ; symbol J) is a derived unit of energy or work in the International System of Units. It is equal to the energy expended in applying a force of one newton through a distance of one metre , or in passing an electric current of one ampere through a resistance of one ohm for one second...
s (6.4 kilocalories burned). Shaving 500 g from the rims/tires/spokes reduces this KE by 35 joules (1 kilocalorie = 1.163 watt-hour
Watt-hour
The kilowatt hour, or kilowatt-hour, is a unit of energy equal to 1000 watt hours or 3.6 megajoules.For constant power, energy in watt hours is the product of power in watts and time in hours...
). The impact of this weight saving on speed or distance is rather difficult to calculate, and requires assumptions about rider power output and sprint distance. The Analytic Cycling web site allows this calculation, and gives a time/distance advantage of 0.16 s/188 cm for a sprinter who shaves 500 g off their wheels. If that weight went to make an aero wheel that was worth 0.03 mph (0.05 km/h) at 25 mph (40 km/h), the weight savings would be canceled by the aerodynamic advantage. For reference, the best aero bicycle wheels are worth about 0.4 mph (0.6 km/h) at 25, and so in this sprint would handily beat a set of wheels weighing 500 g less.
In a criterium race, a rider is often jumping out of every corner. If the rider has to brake entering each corner (no coasting to slow down), then the KE that is added in each jump is wasted as heat in braking. For a flat crit
Criterium
A criterium, or crit, is a bike race held on a short course , often run on closed-off city center streets....
at 40 km/h, 1 km circuit
Race track
A race track is a purpose-built facility for racing of animals , automobiles, motorcycles or athletes. A race track may also feature grandstands or concourses. Some motorsport tracks are called speedways.A racetrack is a permanent facility or building...
, 4 corners per lap, 10 km/h speed loss at each corner, one hour duration, 80 kg rider/6.5 kg bike/1.75 kg rims/tires/spokes, there would be 160 corner jumps. This effort adds 387 kilocalories to the 1100 kilocalories required for the same ride at steady speed. Removing 500 g from the wheels, reduces the total body energy requirement by 4.4 kilocalories. If the extra 500 g in the wheels had resulted in a 0.3% reduction in aerodynamic drag factor (worth a 0.02 mph (0.03 km/h) speed increase at 25 mph), the caloric cost of the added weight effect would be canceled by the reduced work
Mechanical work
In physics, work is a scalar quantity that can be described as the product of a force times the distance through which it acts, and it is called the work of the force. Only the component of a force in the direction of the movement of its point of application does work...
to overcome the wind.
Another place where light wheels are claimed to have great advantage is in climbing. Though one may hear expressions such as "these wheels were worth 1–2 mph", etc. The formula for power
Power (physics)
In physics, power is the rate at which energy is transferred, used, or transformed. For example, the rate at which a light bulb transforms electrical energy into heat and light is measured in watts—the more wattage, the more power, or equivalently the more electrical energy is used per unit...
suggests that 1 lb saved is worth 0.06 mph (0.1 km/h) on a 7% grade, and even a 4 lb saving is worth only 0.25 mph (0.4 km/h) for a light rider. So, where is the big savings in wheel weight reduction coming from? One argument is that there is no such improvement; that it is "placebo effect
Placebo effect
Placebo effect may refer to:* Placebo effect, the tendency of any medication or treatment, even an inert or ineffective one, to exhibit results simply because the recipient believes that it will work...
". But it has been proposed that the speed variation with each pedal
Bicycle pedal
A bicycle pedal is the part of a bicycle that the rider pushes with their foot to propel the bicycle. It provides the connection between the cyclist's foot or shoe and the crank allowing the leg to turn the bottom bracket spindle and propel the bicycle's wheels...
stroke when riding up a hill explains such an advantage. However the energy of speed variation is conserved; during the power phase of pedaling the bike speeds up slightly, which stores KE, and in the "dead spot" at the top of the pedal stroke the bike slows down, which recovers that KE. Thus increased rotating mass may slightly reduce speed variations, but it does not add energy requirement beyond that of the same non-rotating mass.
Lighter bikes are easier to get up hills, but the cost of "rotating mass" is only an issue during a rapid acceleration, and it is small even then.
Explanations
Possible technical explanations for the widely claimed benefits of light components in general, and light wheels in particular, is as follows:- Light weight wins races with significant climbing because the heavier bike can't make up the gap on descents or on the flats: the rider on the lighter bike just draftsDrafting (racing)Drafting or slipstreaming is a technique where two vehicles or other moving objects are caused to align in a close group reducing the overall effect of drag due to exploiting the lead object's slipstream...
. Alternatively, if the identical riders of heavier and lighter bikes simultaneously reach the bottom of a climb to the finish, all of the advantage goes to the lighter bike. This is not the case in a hilly time trialsTeam time trialA team time trial is a road-based bicycle race in which teams of cyclists race against the clock .Teams start at equal intervals, usually two, three or four minutes apart...
(or riding soloIndividual time trialAn individual time trial is a road bicycle race in which cyclists race alone against the clock . There are also track-based time trials where riders compete in velodromes, and team time trials...
), where the advantage of heavier, but more aerodynamic wheels would easily make up the distance lost in climbs. - Light weight wins sprints because it accelerates more easily. But note that heavier aerodynamic wheels gain significant advantage as speed increases, and for a good part of a sprint a rider is doing little accelerating but is working hard against a high-speed wind. So many sprint situations may favor heavier but more aerodynamic wheels.
- Light weight wins in criteriumCriteriumA criterium, or crit, is a bike race held on a short course , often run on closed-off city center streets....
s because of the constant acceleration out of every corner. Heavier but more aerodynamic wheels offer little advantage because the riders are in a group most of the time. The energy savings from lighter wheels is minimal, but it may be more significant that the leg muscles have to put out just that bit of extra effort at each jam.
There are two "non-technical" explanations for the effects of light weight. First is the placebo effect. Since the rider feels that they are on better (lighter) equipment, they push themselves harder and therefore go faster. It's not the equipment that increases speed so much as the rider's belief and resulting higher power output. The second non-technical explanation is the triumph of hope over experience—the rider is not much faster due to lightweight equipment but thinks they are faster. Sometimes this is due to lack of real data, as when a rider took two hours to do a climb on their old bike and on their new bike did it in 1:50. No accounting for how fit
Physical fitness
Physical fitness comprises two related concepts: general fitness , and specific fitness...
the rider was during these two climbs, how hot or windy it was, which way the wind was blowing, how the rider felt that day, etc.
Another explanation, of course, may be marketing
Marketing
Marketing is the process used to determine what products or services may be of interest to customers, and the strategy to use in sales, communications and business development. It generates the strategy that underlies sales techniques, business communication, and business developments...
benefits associated with selling weight reductions.
In the end, the "incremental muscle power requirement" argument is the only one that can support the claimed advantages of light wheels in "jump" situations. This argument would state that: if the rider is already at the limit on each jump or each stroke of the pedals, then the small amount of extra power required for the extra weight would be a significant physiologic
Physiology
Physiology is the science of the function of living systems. This includes how organisms, organ systems, organs, cells, and bio-molecules carry out the chemical or physical functions that exist in a living system. The highest honor awarded in physiology is the Nobel Prize in Physiology or...
burden. Whether this is true is not clear, but it is the only explanation for the claimed advantage of wheel weight savings (compared to saving weight from the rest of the bike). For these accelerations, it makes no difference whether 1 lb is taken off the wheels or 2 lb off the bike/rider. The miracle of light wheels (compared to saving weight anywhere else in the bike/rider system) is hard to see.
Aerodynamics vs power
Heated debates over the relative importance of weight savings and aerodynamics are a fixture in cyclingCycling
Cycling, also called bicycling or biking, is the use of bicycles for transport, recreation, or for sport. Persons engaged in cycling are cyclists or bicyclists...
. This is an attempt to at least get the equation-based parts of the debate clarified. There will always be those who argue that "experience trumps mathematics" on this issue, so this will attempt to highlight those areas where experience might disagree with the math. From this, perhaps further discussion can focus on the topics of dispute rather than questioning known physics. To be as clear as possible, this will cover 1) the power requirements for moving a bike/rider, 2) the energy cost of acceleration, and then 3) why experience and the math might disagree.
Power required
There is a well-known equation that gives the powerPower (physics)
In physics, power is the rate at which energy is transferred, used, or transformed. For example, the rate at which a light bulb transforms electrical energy into heat and light is measured in watts—the more wattage, the more power, or equivalently the more electrical energy is used per unit...
required to push a bike and rider through the air and to overcome the friction of the drive train:
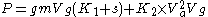
Where
is in wattWatt
The watt is a derived unit of power in the International System of Units , named after the Scottish engineer James Watt . The unit, defined as one joule per second, measures the rate of energy conversion.-Definition:...
s,
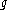is Earth's gravityEarth's gravity
The gravity of Earth, denoted g, refers to the acceleration that the Earth imparts to objects on or near its surface. In SI units this acceleration is measured in metres per second per second or equivalently in newtons per kilogram...
,
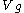is ground speed (m/s), 
is bike/rider mass in kg, 
is the grade (m/m), and 
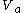is the rider's speed through the air (m/s). 
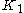is a lumped constant for all frictionFriction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...
al losses (tires, bearings, chain), and is generally reported with a value of 0.0053.
is a lumped constant for aerodynamic drag and is generally reported with a value of 0.185 kg/m.Note that the power required to overcome friction and gravity is proportional only to rider weight and ground speed. The aerodynamic drag is roughly proportional to the square of the relative velocity of the air and the bike. Being that the total power requirement to propel the bike forward is a sum of these two variables multiplied by speed, the degree of proportionality between power requirement and speed varies according to their relative magnitude, in an interval between the linear and cube: at higher speeds (riding fast on a flat road) power required will be close to being a cube function of speed, at lower speeds (climbing a steep hill) it will be close to being a linear function of speed.
The human body runs at about 24% efficiency for a relatively fit athlete, so for every kilojoule delivered to the pedals the body consumes 1 kcal (4.2 kJ) of food energy.
Obviously, both of the lumped constants in this equation depend on many variables, including drive train efficiency, the rider's position and drag area, aerodynamic equipment, tire pressure, and road surface
Pavement (material)
Road surface or pavement is the durable surface material laid down on an area intended to sustain vehicular or foot traffic, such as a road or walkway. In the past cobblestones and granite setts were extensively used, but these surfaces have mostly been replaced by asphalt or concrete. Such...
. Also, recognize that air speed is not constant in speed or direction or easily measured. It is certainly reasonable that the aerodynamic lumped constant would be different in cross winds or tail winds than in direct head winds, as the profile the bike/rider presents to the wind is different in each situation. Also, wind speed
Wind speed
Wind speed, or wind velocity, is a fundamental atmospheric rate.Wind speed affects weather forecasting, aircraft and maritime operations, construction projects, growth and metabolism rate of many plant species, and countless other implications....
as seen by the bike/rider is not uniform except in zero wind conditions. Weather report
Weather forecasting
Weather forecasting is the application of science and technology to predict the state of the atmosphere for a given location. Human beings have attempted to predict the weather informally for millennia, and formally since the nineteenth century...
wind speed is measured at some distance above the ground in free air with no obstructing trees or buildings nearby. Yet, by definition, the wind speed is always zero right at the road surface. Assuming a single wind velocity and a single lumped drag constant are just two of the simplifying assumptions of this equation. Computational fluid dynamicists
Computational fluid dynamics
Computational fluid dynamics, usually abbreviated as CFD, is a branch of fluid mechanics that uses numerical methods and algorithms to solve and analyze problems that involve fluid flows. Computers are used to perform the calculations required to simulate the interaction of liquids and gases with...
have looked at this bicycle modeling problem and found it hard to model well. In layman's terms, this means that much more sophisticated models can be developed, but they will still have simplifying assumptions.
Given this simplified equation, however, one can calculate some values of interest. For example, assuming no wind, one gets the following results for kilocalories required and power delivered to the pedals (watts):
- 175 W for a 90 kg bike + rider to go 9 m/s (20 mph or 32 km/h) on the flats (76% of effort to overcome aerodynamic drag), or 2.6 m/s (5.8 mph or 9.4 km/h) on a 7% grade (21% of effort to overcome aerodynamic drag).
- 300 W for a 90 kg bike + rider at 11 m/s (25 mph or 40 km/h) on the flats (83% of effort to overcome aerodynamic drag) or 4.3 m/s (9.5 mph or 15 km/h) on a 7% grade (42% of effort to overcome aerodynamic drag).
- 165 W for a 65 kg bike + rider to go 9 m/s (20 mph or 32 km/h) on the flats (82% of effort to overcome aerodynamic drag), or 3.3 m/s (7.4 mph or 12 km/h) on a 7% grade (37% of effort to overcome aerodynamic drag).
- 285 W for a 65 kg bike + rider at 11 m/s (25 mph or 40 km/h) on the flats (87% of effort to overcome aerodynamic drag) or 5.3 m/s (12 mph or 19 km/h) on a 7% grade (61% of effort to overcome aerodynamic drag).
Shaving 1 kg off the weight of the bike/rider would increase speed by 0.01 m/s at 9 m/s on the flats (5 seconds in a 20 mph (32 km/h), 25-mile (40 km) TT). Losing 1 kg on a 7% grade would be worth 0.04 m/s (90 kg bike + rider) to 0.07 m/s (65 kg bike + rider). If one climbed for 1 hour, saving 1 lb would gain between 225 and 350 feet (107 m) – less effect for the heavier bike + rider combination (e.g., 0.04 mph (0.06 km/h) * 1 h * 5,280 ft (1,609 m)/mi = 225 ft). For reference, the big climbs in the Tour de France
Tour de France
The Tour de France is an annual bicycle race held in France and nearby countries. First staged in 1903, the race covers more than and lasts three weeks. As the best known and most prestigious of cycling's three "Grand Tours", the Tour de France attracts riders and teams from around the world. The...
have the following average grades:
- TourmaletCol du TourmaletCol du Tourmalet is the highest road in the central Pyrenees in the department of Hautes-Pyrénées in France. Sainte-Marie-de-Campan is at the foot on the eastern side and the ski station La Mongie two-thirds of the way up. Luz-Saint-Sauveur is at the bottom of the western side.Tourmalet is also a...
= 7% - GalibierCol du GalibierCol du Galibier is a mountain pass in the southern region of the French Dauphiné Alps near Grenoble. It is the ninth highest paved road in the Alps and the sixth highest mountain pass. It is often the highest point of the Tour de France....
= 7.5% - Alpe D'HuezAlpe d'HuezL'Alpe d'Huez is a ski resort at . It is a mountain pasture in the Central French Alps, in the commune of Huez, in the Isère département in the Rhône-Alpes region.-Tour de France:L'Alpe d'Huez is one of the main mountains in the Tour de France...
= 8.6% - Mont VentouxMont VentouxMont Ventoux is a mountain in the Provence region of southern France, located some 20 km northeast of Carpentras, Vaucluse. On the north side, the mountain borders the Drôme département. It is the largest mountain in the region and has been nicknamed the "Giant of Provence", or "The Bald...
= 7.1%.
The equation can be separated into level ground power
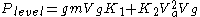,and vertical climbing power given by
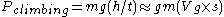.See also
- BicycleBicycleA bicycle, also known as a bike, pushbike or cycle, is a human-powered, pedal-driven, single-track vehicle, having two wheels attached to a frame, one behind the other. A person who rides a bicycle is called a cyclist, or bicyclist....
- Bicycle and motorcycle dynamicsBicycle and motorcycle dynamicsBicycle and motorcycle dynamics is the science of the motion of bicycles and motorcycles and their components, due to the forces acting on them. Dynamics is a branch of classical mechanics, which in turn is a branch of physics. Bike motions of interest include balancing, steering, braking,...
- Cycling power meterCycling power meterA cycling power meter is a device on a bicycle that allows measuring of the power output of the rider. Most cycling power meters use strain gauges to measure torque applied, and, combined with angular velocity, calculate power...
- CyclocomputerCyclocomputerA cyclocomputer or cyclometer is a device mounted on a bicycle that calculates and displays trip information, similar to the instruments in the dashboard of a car. The computer with display, or head unit, usually is attached to the handlebar for easy viewing.-History:In 1895 Curtis Hussey Veeder...