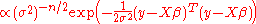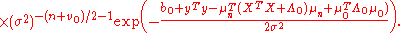Bayesian linear regression
Encyclopedia
In statistics
, Bayesian linear regression is an approach to linear regression
in which the statistical analysis is undertaken within the context of Bayesian inference
. When the regression model has errors
that have a normal distribution, and if a particular form of prior distribution is assumed, explicit results are available for the posterior probability distributions of the model's parameters.
problem, in which for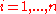
we specify the conditional distribution
of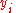
given a 
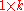predictor vector 
:
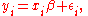
where
is a 
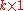vector, and the 
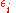is independent and identically-distributed and normally distributed random variables:
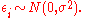
This corresponds to the following likelihood function
:
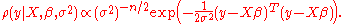
The ordinary least squares
solution is to estimate the coefficient vector using the Moore-Penrose pseudoinverse:
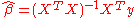
where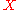
is the 
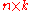design matrix
, each row of which is a predictor vector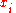
; and 
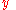is the column 
-vector 
.
This is a frequentist approach, and it assumes that there are enough measurements to say something meaningful about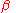
. In the Bayesian
approach, the data are supplemented with additional information in the form of a prior probability distribution. The prior belief about the parameters is combined with the data's likelihood function according to Bayes theorem to yield the posterior belief
about the parameters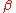
and 
. The prior can take different functional forms depending on the domain and the information that is available a priori.
for which the posterior distribution can be derived analytically.
A prior
is conjugate
to this likelihood function if it has of the same functional form with respect to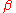
and 
. Since the log-likelihood is quadratic in 
, the log-likelihood is re-written such that the likelihood becomes normal in 
. Write
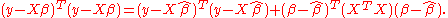
The likelihood as is now re-written as
where
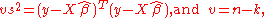
with
as the number of parameters to estimate.
This suggests a form for the prior:
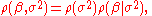
where
is an inverse-gamma distribution
and
is a normal distribution
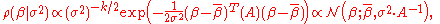
with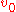
and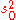 
as the prior values of 
and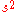 
, respectively.
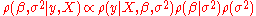
With some re-arrangement, the posterior can be re-written so that the posterior mean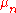
of the parameter vector 
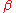can be expressed in terms of the least squares estimator 
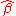and the prior mean 
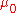, with the strength of the prior indicated by the prior precision matrix 
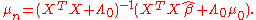
To justify that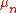
is indeed the posterior mean, the quadratic terms in the exponential can be re-arranged as a quadratic form
in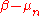
.
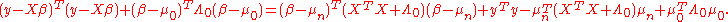
Now the posterior can be expressed as a normal distribution
times an inverse-gamma distribution:
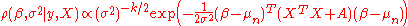
Therefore the posterior distribution can be parametrized as follows.
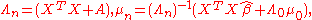
This can be interpreted as Bayesian learning where the parameters are updated according to the following equations.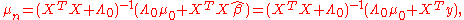
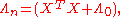
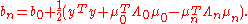
In this article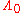
is called 
.
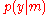is the probability of the data given the model 
. It is also known as the marginal likelihood
, and as the prior predictive density. Here, the model is defined by the likelihood function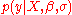
and the prior distribution on the parameters, i.e. 
. The model evidence captures in a single number how well such a model explains the observations. The model evidence of the Bayesian linear regression model presented in this section can be used to compare competing linear models by Bayesian model comparison. These models may differ in the number and values of the predictor variables as well as in their priors on the model parameters. Model complexity is already taken into account by the model evidence, because it marginalizes out the parameters by integrating 
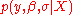over all possible values of 
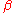and 
.
This integral can be computed analytically and the solution is given in the following equation.
Here
denotes the gamma function
. Because we have chosen a conjugate prior, the marginal likelihood can also be easily computed by evaluating the following equality for arbitrary values of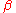
and 
.
Note that this equation is nothing but a re-arrangement of Bayes theorem. Inserting the formulas for the prior, the likelihood, and the posterior and simplifying the resulting expression leads to the analytic expression given above.
method such as Monte Carlo sampling or variational Bayes
.
The special case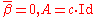
is called ridge regression.
A similar analysis can be performed for the general case of the multivariate regression and part of this provides for Bayesian estimation of covariance matrices
: see Bayesian multivariate linear regression.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, Bayesian linear regression is an approach to linear regression
Linear regression
In statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
in which the statistical analysis is undertaken within the context of Bayesian inference
Bayesian inference
In statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
. When the regression model has errors
Errors and residuals in statistics
In statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
that have a normal distribution, and if a particular form of prior distribution is assumed, explicit results are available for the posterior probability distributions of the model's parameters.
Model setup
Consider a standard linear regressionLinear regression
In statistics, linear regression is an approach to modeling the relationship between a scalar variable y and one or more explanatory variables denoted X. The case of one explanatory variable is called simple regression...
problem, in which for
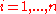we specify the conditional distributionConditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
of
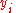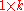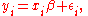
given a predictor vector :where
is a 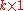vector, and the 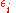is independent and identically-distributed and normally distributed random variables: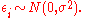This corresponds to the following likelihood function
Likelihood function
In statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
:
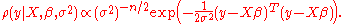
The ordinary least squares
Ordinary least squares
In statistics, ordinary least squares or linear least squares is a method for estimating the unknown parameters in a linear regression model. This method minimizes the sum of squared vertical distances between the observed responses in the dataset and the responses predicted by the linear...
solution is to estimate the coefficient vector using the Moore-Penrose pseudoinverse:
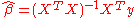
where
is the 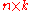design matrixDesign matrix
In statistics, a design matrix is a matrix of explanatory variables, often denoted by X, that is used in certain statistical models, e.g., the general linear model....
, each row of which is a predictor vector
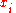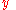; and is the column -vector .This is a frequentist approach, and it assumes that there are enough measurements to say something meaningful about
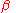. In the BayesianBayesian inference
In statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
approach, the data are supplemented with additional information in the form of a prior probability distribution. The prior belief about the parameters is combined with the data's likelihood function according to Bayes theorem to yield the posterior belief
Posterior probability
In Bayesian statistics, the posterior probability of a random event or an uncertain proposition is the conditional probability that is assigned after the relevant evidence is taken into account...
about the parameters
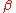and . The prior can take different functional forms depending on the domain and the information that is available a priori.Conjugate prior distribution
For an arbitrary prior distribution, there may be no analytical solution for the posterior distribution. In this section, we will consider a so called conjugate priorConjugate prior
In Bayesian probability theory, if the posterior distributions p are in the same family as the prior probability distribution p, the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood...
for which the posterior distribution can be derived analytically.
A prior
is conjugateConjugate prior
In Bayesian probability theory, if the posterior distributions p are in the same family as the prior probability distribution p, the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood...
to this likelihood function if it has of the same functional form with respect to
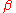and . Since the log-likelihood is quadratic in , the log-likelihood is re-written such that the likelihood becomes normal in . Write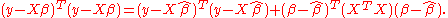The likelihood as is now re-written as
where
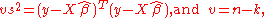
with
as the number of parameters to estimate.This suggests a form for the prior:
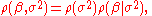
where
is an inverse-gamma distributionand
is a normal distribution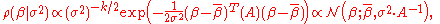with
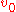and 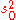as the prior values of and 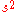, respectively.Posterior distribution
With the prior now specified, the posterior distribution can be expressed as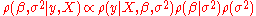
With some re-arrangement, the posterior can be re-written so that the posterior mean
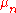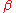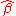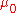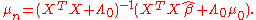
of the parameter vector can be expressed in terms of the least squares estimator and the prior mean , with the strength of the prior indicated by the prior precision matrix To justify that
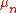is indeed the posterior mean, the quadratic terms in the exponential can be re-arranged as a quadratic formQuadratic form (statistics)
If \epsilon is a vector of n random variables, and \Lambda is an n-dimensional symmetric matrix, then the scalar quantity\epsilon^T\Lambda\epsilonis known as a quadratic form in \epsilon.-Expectation:It can be shown that...
in
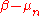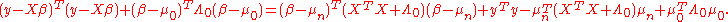
.Now the posterior can be expressed as a normal distribution
times an inverse-gamma distribution:
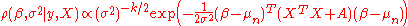
Therefore the posterior distribution can be parametrized as follows.
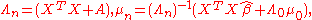
This can be interpreted as Bayesian learning where the parameters are updated according to the following equations.
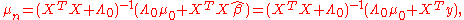
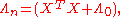
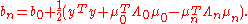
In this article
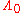is called .Model evidence
The model evidence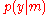 is the probability of the data given the model . It is also known as the marginal likelihoodMarginal likelihood
In statistics, a marginal likelihood function, or integrated likelihood, is a likelihood function in which some parameter variables have been marginalised...
, and as the prior predictive density. Here, the model is defined by the likelihood function
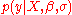and the prior distribution on the parameters, i.e. . The model evidence captures in a single number how well such a model explains the observations. The model evidence of the Bayesian linear regression model presented in this section can be used to compare competing linear models by Bayesian model comparison. These models may differ in the number and values of the predictor variables as well as in their priors on the model parameters. 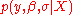Model complexity is already taken into account by the model evidence, because it marginalizes out the parameters by integrating over all possible values of 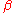and .This integral can be computed analytically and the solution is given in the following equation.
Here
denotes the gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
. Because we have chosen a conjugate prior, the marginal likelihood can also be easily computed by evaluating the following equality for arbitrary values of
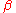and .Note that this equation is nothing but a re-arrangement of Bayes theorem. Inserting the formulas for the prior, the likelihood, and the posterior and simplifying the resulting expression leads to the analytic expression given above.
Other cases
In general, it may be impossible or impractical to derive the posterior distribution analytically. However, it is possible to approximate the posterior by an approximate Bayesian inferenceApproximate Bayesian computation
Approximate Bayesian computation is a family of computational techniques in Bayesian statistics. These simulation techniques operate on summary data to make broad inferences with less computation than might be required if all available data were analyzed in detail...
method such as Monte Carlo sampling or variational Bayes
Variational Bayes
Variational Bayesian methods, also called ensemble learning, are a family of techniques for approximating intractable integrals arising in Bayesian inference and machine learning...
.
The special case
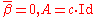is called ridge regression.A similar analysis can be performed for the general case of the multivariate regression and part of this provides for Bayesian estimation of covariance matrices
Estimation of covariance matrices
In statistics, sometimes the covariance matrix of a multivariate random variable is not known but has to be estimated. Estimation of covariance matrices then deals with the question of how to approximate the actual covariance matrix on the basis of a sample from the multivariate distribution...
: see Bayesian multivariate linear regression.
See also
- Bayesian estimation of linear models (R programming wikibook). Bayesian linear regression as pre implemented in RR (programming language)R is a programming language and software environment for statistical computing and graphics. The R language is widely used among statisticians for developing statistical software, and R is widely used for statistical software development and data analysis....
. - Bayes linear statistics